反プリズムグラフ
数学のグラフ理論分野において、反プリズムグラフとは、反プリズムの1つを骨格とするグラフである。n面反プリズムは2n個の頂点と4n個の辺を持つ。これらは正則グラフ、多面体グラフ(したがって必然的に3頂点連結グラフ、頂点推移グラフ、平面グラフでもある)、そしてハミルトングラフでもある。[ 1 ]
例
数列の最初のグラフである四面体グラフは、4つの頂点と6つの辺を持ちます。2番目のグラフである八面体グラフは、6つの頂点と12の辺を持ちます。数列の後半のグラフは、対応する反プリズムの種類にちなんで名付けられています。
- 正方反角柱グラフ – 8頂点、16辺
- 五角形逆柱状グラフ – 10頂点、20辺
- 六角形逆柱状グラフ – 12頂点、24辺
- 七角形逆柱状グラフ – 14頂点、28辺
- 八角形の逆柱状グラフ – 16頂点、32辺
- ...
 2 2 | 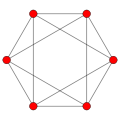 3 3 |  4 4 |  5 5 |  6 6 |  7 7 |  8 8 |
幾何学的には、星型多角形は、(自己交差する)異なる一連の反プリズム(星型反プリズム)の面も形成しますが、異なる一連のグラフは形成しません。
関連グラフ
反プリズムグラフは循環グラフCi 2 n (2,1) の特殊なケースである。
正多角形を底とする多面体から同様に形成される多面体グラフの無限列には、プリズムグラフ(プリズムのグラフ)やホイールグラフ(ピラミッドのグラフ)などがあります。頂点推移的な多面体グラフには、アルキメデスグラフなどがあります。
参考文献
- ^ Read, RCおよびWilson, RJ An Atlas of Graphs、オックスフォード、イギリス:オックスフォード大学出版局、2004年再版、第6章特殊グラフpp. 261, 270。
外部リンク
- Weisstein, Eric W. 「反プリズムグラフ」。MathWorld 。