アポロニウスの円は、著名なギリシャの幾何学者、ペルガのアポロニウスに関連するいくつかの円の集合のいずれかです。これらの円のほとんどは平面ユークリッド幾何学に見られます が、類似の円は他の面にも定義されています。 例えば、球面上の対応する円は、立体射影によって定義できます
この用語の主な用途は次の 5 つです。
- アポロニウスは、円は平面上の点の集合であり、焦点と呼ばれる2つの固定点から特定の距離比を持つ点の集合として定義できることを示しました。このアポロニウスの円は、アポロニウスの追跡問題の基礎です。これは、#2で説明した最初の族の特殊なケースです。
- アポロニアン円は、互いに直交する円の2つの族です。最初の族は、2つの固定焦点(#1と同じ円)に対するあらゆる距離比を持つ円から成り、2番目の族は、両方の焦点を通るあらゆる円から成ります。これらの円は双極座標の基礎となります。
- 三角形のアポロニウスの円は3つの円から成り、それぞれが三角形の1つの頂点を通り、他の2つの頂点との距離比が一定です。これらのアポロニウスの円を用いて、三角形の等力点とルモワーヌ線を解くことができます。
- アポロニウスの問題は、指定された3つの円に同時に接する円を描くことです。この問題の解は、アポロニウスの円と呼ばれることもあります。
- アポロニウスのガスケットは、これまでに記述された最初のフラクタルの一つであり、アポロニウスの問題を繰り返し解くことによって形成される、互いに接する円の集合です。
アポロニウスによる円の定義
 アポロニウスによる円の定義
アポロニウスによる円の定義円は通常、ある点(円の中心)からある距離r(円の半径)にある点Pの集合として定義されます。しかし、円には他にも同等の定義があります。アポロニウスは、円は距離の比k = にある点Pの集合として定義できることを発見しました。d 1/d 2与えられた2点(図ではAとBと表記)への投影。これらの2点は焦点と 呼ばれることもあります
ユークリッド空間におけるベクトルを用いた証明
d 1、d 2 を等しくない正の実数とする。CをABの内分点( d 1 : d 2の比)とし、DをABの外分点( d 1 : d 2 の比)とする。

そして、

したがって、点Pは直径CDの円上にあります
角の二等分線定理を用いた証明
 アポロニウスの円の定義の証明
アポロニウスの円の定義の証明まず、との間の線分上の点を考えます。この線分上の点において、 の比が成り立ちます。 の定義 との二等分線定理 の逆から、 の角度と の角度は等しくなります。 





次に、延長線上で比を満たす もう一つの点を取ります。したがって、延長線上の任意 の点も取ります。角の二等分線定理の逆により、直線は外角を二等分します。したがって、とは等しく、 です。したがって、タレスの定理により、 は直径 を 持つ円上に存在します。











アポロニウスの追跡問題
アポロニウスの追跡問題は、ある地点Aから速度v Aで出発する船が、別の地点Bから速度v Bで出発する別の船を迎撃するかどうかを求める問題です。2隻の船が迎撃するまでの最短時間は、直線経路を用いて計算されます。船の速度が一定に保たれている場合、速度比はμで定義されます。両方の船が将来の地点Iで衝突または出会った場合、それぞれの距離は次の式で表されます。[ 1 ]

両辺を二乗すると次のようになります。



![{\displaystyle x^{2}+y^{2}=[(dx)^{2}+y^{2}]\mu^{2}}](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
拡大:
![{\displaystyle x^{2}+y^{2}=[d^{2}+x^{2}-2dx+y^{2}]\mu^{2}}](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
さらに拡大:

左側に移動:

因数分解:

割る : 

平方完成:

非平方項を右辺に移動します。

そして:

したがって、その点は、アポロニウスによって定義された円上にあり、その始点を焦点とする必要があります
根軸を共有する円
 アポロニウスの円の集合。すべての青い円はすべての赤い円と直角に交わり、またその逆も同様です。すべての赤い円は2つの焦点を通り、上の図の点Aと点Bに相当します。
アポロニウスの円の集合。すべての青い円はすべての赤い円と直角に交わり、またその逆も同様です。すべての赤い円は2つの焦点を通り、上の図の点Aと点Bに相当します。アポロニアン追跡問題によって同じ 2 点AとBに対して定義される円のうち、2 つの速度の比率が異なる円は、互いに分離しており、平面全体を覆う連続した族を形成します。この円族は双曲線鉛筆として知られています。もう 1 つの円族、つまりAとBの両方を通る円も鉛筆、より正確には楕円鉛筆と呼ばれます。これらの 2 つのアポロニアン円鉛筆は直角に交差し、双極座標系の基礎を形成します。各鉛筆内では、任意の 2 つの円が同じ根軸を持ちます。つまり、2 つの鉛筆の 2 つの根軸は直交し、一方の鉛筆の円の中心はもう一方の鉛筆の根軸上にあります。
アポロニウスの問題の解決策
 アポロニウスの問題には最大8つの解が存在する可能性があります。3つの与円は黒で示され、解円は色付きで示されています。
アポロニウスの問題には最大8つの解が存在する可能性があります。3つの与円は黒で示され、解円は色付きで示されています。ユークリッド平面幾何学において、アポロニウスの問題は、平面上の 3 つの与えられた円に 接する円を描くことです。
3 つの与えられた円には、一般に、それらに接する 8 つの異なる円があり、各解円は、3 つの与えられた円を異なる方法で囲むか除外します。つまり、各解では、3 つの円の異なるサブセットが囲まれます。
アポロニウスのガスケット
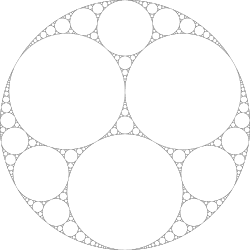
 対称的なアポロニアンガスケット。発明者のゴットフリート・ライプニッツにちなんで、ライプニッツパッキングとも呼ばれます
対称的なアポロニアンガスケット。発明者のゴットフリート・ライプニッツにちなんで、ライプニッツパッキングとも呼ばれますアポロニウスの問題を繰り返し解いて内接円を求めると、互いに接する円の隙間を任意に細かく埋めることができ、ライプニッツ パッキングまたはアポロニアン パッキングとも呼ばれるアポロニアン ガスケットが形成される。[ 2 ] このガスケットはフラクタルであり、自己相似性があり、次元dは正確にはわかっていないがおよそ 1.3 である。 [ 3 ]これは、通常の(または修正可能な) 曲線の次元 ( d = 1)よりも高い が、平面の次元 ( d = 2) よりも低い。アポロニウスのガスケットは、17 世紀にゴットフリート ライプニッツ によって初めて記述され、20 世紀のシェルピンスキーの三角形の曲線の前身である。[ 4 ] アポロニウスのガスケットは、数学の他の分野とも深いつながりがある。例えば、クライン群の極限集合である。[ 5 ]円充填定理も参照。
三角形の等力点
アポロニウスの円は、任意の三角形 によって定義される3つの特別な円を表すこともあります。円は、三角形の頂点を通り、他の2つの頂点およびとの距離の比が一定である唯一の円として定義されます(上記のアポロニウスによる円の定義を参照)。同様に、円は、三角形の頂点を通り、他の2つの頂点およびとの距離の比が一定である唯一の円として定義され、円 についても同様です。 










3つの円はすべて、三角形の外接円と直交します。3つの円はすべて2点を通過し、これらは三角形の等力点とと呼ばれます。これらの共通交点を結ぶ線は、 3つの円すべての根軸です。2つの等力点は、三角形の 外接円に対して互いに逆の関係にあります。

これら3つの円の中心は、単一の直線(ルモワーヌ線)上に位置します。この直線は、等力点によって決定される直線である根軸に垂直です。
参照
参考文献
- ^ Weintraub, Isaac; Garcia, Eloy; Pachter, Meir (2020). 「3次元における非機動目標の防御のための最適誘導戦略」 . IET Control Theory & Applications . 14 (11): 1531– 1538. doi : 10.1049/iet-cta.2019.0541 .
- ^ Kasner, E.; Supnick, F. (1943). 「アポロニアン円パッキング」 . Proceedings of the National Academy of Sciences USA . 29 (11): 378– 384. Bibcode : 1943PNAS...29..378K . doi : 10.1073 / pnas.29.11.378 . PMC 1078636. PMID 16588629 .
- ^ Boyd, David W. (1973). 「ディスクパッキング定数の改良された境界値」. Aequationes Mathematicae . 9 : 99–106 . doi : 10.1007/BF01838194 . S2CID 121089590 . Boyd, David W. (1973). 「アポロニアンパッキングの残差集合次元」. Mathematika . 20 (2): 170–174 . doi : 10.1112/S0025579300004745 .McMullen, Curtis, T. (1998). 「ハウスドルフ次元と共形力学 III:次元の計算」(PDF) . American Journal of Mathematics . 120 (4): 691– 721. doi : 10.1353/ajm.1998.0031 . S2CID 15928775 .
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^マンデルブロ, B. (1983). 『自然のフラクタル幾何学』ニューヨーク: WH Freeman. p. 170. ISBN 978-0-7167-1186-5。アステ、T.、ウィア、D. (2008). 『完璧な梱包の追求』(第2版). ニューヨーク:テイラー・アンド・フランシス. pp. 131-138 . ISBN 978-1-4200-6817-7。
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^マムフォード、D.、シリーズ、C.、およびライト、D. (2002).インドラの真珠:フェリックス・クラインのビジョン. ケンブリッジ:ケンブリッジ大学出版局. pp. 196–223 . ISBN 0-521-35253-3。
{{cite book}}: CS1 maint: multiple names: authors list (link)
参考文献




























![{\displaystyle x^{2}+y^{2}=[(dx)^{2}+y^{2}]\mu^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e050060e3159224d3bad310f31ca46f0ef2036cd)
![{\displaystyle x^{2}+y^{2}=[d^{2}+x^{2}-2dx+y^{2}]\mu^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adc0c5e30a7dafa4b341bce639fb39f52254dc7a)


















