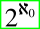Code (set theory)

In set theory, a code for a hereditarily countable set

${\displaystyle x\in H_{\aleph _{1}}\,}$

is a set

${\displaystyle E\subset \omega \times \omega }$

such that there is an isomorphism between ${\displaystyle (\omega ,E)}$ and ${\displaystyle (X,\in )}$ where ${\displaystyle X}$ is the transitive closure of ${\displaystyle \{x\}}$ .^[1] If ${\displaystyle X}$ is finite (with cardinality ${\displaystyle n}$ ), then use ${\displaystyle n\times n}$ instead of ${\displaystyle \omega \times \omega }$ and ${\displaystyle (n,E)}$ instead of ${\displaystyle (\omega ,E)}$ .

According to the axiom of extensionality, the identity of a set is determined by its elements. And since those elements are also sets, their identities are determined by their elements, etc.. So if one knows the element relation restricted to ${\displaystyle X}$ , then one knows what ${\displaystyle x}$ is. (We use the transitive closure of ${\displaystyle \{x\}}$ rather than of ${\displaystyle x}$ itself to avoid confusing the elements of ${\displaystyle x}$ with elements of its elements or whatever.) A code includes that information identifying ${\displaystyle x}$ and also information about the particular injection from ${\displaystyle X}$ into ${\displaystyle \omega }$ which was used to create ${\displaystyle E}$ . The extra information about the injection is non-essential, so there are many codes for the same set which are equally useful.

So codes are a way of mapping ${\displaystyle H_{\aleph _{1}}}$ into the powerset of ${\displaystyle \omega \times \omega }$ . Using a pairing function on ${\displaystyle \omega }$ such as ${\displaystyle (n,k)\mapsto (n^{2}+2nk+k^{2}+n+3k)/2}$ , we can map the powerset of ${\displaystyle \omega \times \omega }$ into the powerset of ${\displaystyle \omega }$ . And we can map the powerset of ${\displaystyle \omega }$ into the Cantor set, a subset of the real numbers. So statements about ${\displaystyle H_{\aleph _{1}}}$ can be converted into statements about the reals. Therefore, ${\displaystyle H_{\aleph _{1}}\subset L(R)}$ , where L(R) is the smallest transitive inner model of ZF containing all the ordinals and all the reals.

Codes are useful in constructing mice.

References

1. Mitchell, William J. (1998), "The complexity of the core model", The Journal of Symbolic Logic, 63 (4): 1393–1398, arXiv:math/9210202, doi:10.2307/2586656, JSTOR 2586656, MR 1665735