ファノフロー
Fluid flow through a constant-area duct with friction

流体力学において、ファノ流れ（イタリアの技術者ジーノ・ジローラモ・ファノにちなんで）は、一定面積のダクトを通る断熱流れで、摩擦の影響が考慮される。[1] ファノ流れモデルは非圧縮性流れにも確実に適用されるが、圧縮性の影響がしばしば考慮される。このモデルでは、ダクト面積は一定で、流れは定常かつ1次元であると仮定され、ダクト内に質量は加えられない。ファノ流れモデルは、粘性効果による不可逆プロセスであると考えられる。粘性摩擦により、流れの特性がダクトに沿って変化する。摩擦効果は、ダクトのどの断面でも均一な特性を持つ流体に作用する壁面 せん断応力としてモデル化される。

十分に長いダクト内において、上流マッハ数が1.0を超える流れでは減速が生じ、流れが閉塞する可能性があります。一方、上流マッハ数が1.0未満の流れでは加速が生じ、十分に長いダクト内において流れが閉塞する可能性があります。熱量的に完全な気体の流れでは、 M  = 1.0 で最大エントロピーが生じることが示されています。

理論

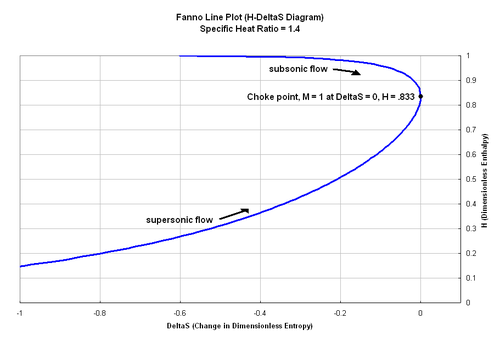
図1ファノ線は無次元H-ΔS軸上にプロットされます。

ファノ流れモデルは、ダクトの長さdM/dxに対するマッハ数の変化を関連付ける微分方程式から始まります。この微分方程式の他の項は、熱容量比γ、ファニング摩擦係数f、水力直径D hです。

  d M 2 M 2 = γ M 2 1 − M 2 ( 1 + γ − 1 2 M 2 ) 4 f D h d x {\displaystyle \ {\frac {dM^{2}}{M^{2}}}={\frac {\gamma M^{2}}{1-M^{2}}}\left(1+{\frac {\gamma -1}{2}}M^{2}\right){\frac {4f}{D_{h}}}dx}

ファニング摩擦係数がダクト壁に沿って一定であると仮定すると、微分方程式は容易に解くことができます。[2] [3]しかし、超音速、特に極超音速の流速 では、ファニング摩擦係数の値を決定することが難しい場合があることに留意する必要があります。結果として得られる関係式を以下に示します。ここで、 L*は上流マッハ数が超音速であると仮定した場合、流れをチョークするために必要なダクト長さです。左辺はしばしばファノパラメータと呼ばれます。

  4 f L ∗ D h = ( 1 − M 2 γ M 2 ) + ( γ + 1 2 γ ) ln ⁡ [ M 2 ( 2 γ + 1 ) ( 1 + γ − 1 2 M 2 ) ] {\displaystyle \ {\frac {4fL^{*}}{D_{h}}}=\left({\frac {1-M^{2}}{\gamma M^{2}}}\right)+\left({\frac {\gamma +1}{2\gamma }}\right)\ln \left[{\frac {M^{2}}{\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)}}\right]}

ファノフローモデルにとって同様に重要なのは、一定圧力での熱容量c pに対するエントロピーの変化の無次元比です。

  Δ S = Δ s c p = ln ⁡ [ M γ − 1 γ ( [ 2 γ + 1 ] [ 1 + γ − 1 2 M 2 ] ) − ( γ + 1 ) 2 γ ] {\displaystyle \ \Delta S={\frac {\Delta s}{c_{p}}}=\ln \left[M^{\frac {\gamma -1}{\gamma }}\left(\left[{\frac {2}{\gamma +1}}\right]\left[1+{\frac {\gamma -1}{2}}M^{2}\right]\right)^{\frac {-(\gamma +1)}{2\gamma }}\right]}

上記の式は、静的温度とよどみ点温度の比で書き直すことができ、これは熱量的に完全な気体の場合、無次元エンタルピー比Hに等しい。

  H = h h 0 = c p T c p T 0 = T T 0 {\displaystyle \ H={\frac {h}{h_{0}}}={\frac {c_{p}T}{c_{p}T_{0}}}={\frac {T}{T_{0}}}}
  Δ S = Δ s c p = ln ⁡ [ ( 1 H − 1 ) γ − 1 2 γ ( 2 γ − 1 ) γ − 1 2 γ ( γ + 1 2 ) γ + 1 2 γ ( H ) γ + 1 2 γ ] {\displaystyle \ \Delta S={\frac {\Delta s}{c_{p}}}=\ln \left[\left({\frac {1}{H}}-1\right)^{\frac {\gamma -1}{2\gamma }}\left({\frac {2}{\gamma -1}}\right)^{\frac {\gamma -1}{2\gamma }}\left({\frac {\gamma +1}{2}}\right)^{\frac {\gamma +1}{2\gamma }}\left(H\right)^{\frac {\gamma +1}{2\gamma }}\right]}

上記の式は、 H - ΔS図上で与えられたファンノ流れの状態軌跡を表すファンノ線をプロットするために使用できます。図では、ファンノ線はH  = 0.833で最大エントロピーに達し、流れはチョーク状態にあります。熱力学第二法則によれば、ファンノ流れではエントロピーは常に増加しなければなりません。これは、摩擦を伴うダクトに流入する亜音速流れは、流れがチョーク状態になるまでマッハ数が増加し続けることを意味します。逆に、超音速流れのマッハ数は流れがチョーク状態になるまで減少します。ファンノ線上の各点は異なるマッハ数に対応しており、チョーク状態への動きが図に示されています。

ファノ線は、質量流量と全エンタルピーが一定に保たれ、運動量が変化する場合に、気体が取り得る状態を定義します。ファノ線上の各点は異なる運動量を持ち、運動量の変化は摩擦の影響によるものです。[4]

追加のファノフロー関係

図 2 Fanno フロー モデルを使用してマッハ数の関数としてプロットされた一般的な熱力学特性比。

前述の通り、ファノ流れではダクト内の面積と質量流量は一定に保たれます。さらに、よどみ点温度も一定です。これらの関係は以下に示されており、*記号はチョークが発生する可能性のあるスロート位置を表しています。よどみ点特性には添え字0が含まれます。

A = A ∗ = constant T 0 = T 0 ∗ = constant m ˙ = m ˙ ∗ = constant {\displaystyle {\begin{aligned}A&=A^{*}={\mbox{constant}}\\T_{0}&=T_{0}^{*}={\mbox{constant}}\\{\dot {m}}&={\dot {m}}^{*}={\mbox{constant}}\end{aligned}}}

微分方程式を展開し、解くことで、チョーク位置における値に対するファノ流動特性比を記述することもできます。圧力、密度、温度、速度、よどみ点圧力の比はそれぞれ以下に示されています。これらはファノパラメータとともにグラフで表されています。

p p ∗ = 1 M 1 ( 2 γ + 1 ) ( 1 + γ − 1 2 M 2 ) ρ ρ ∗ = 1 M ( 2 γ + 1 ) ( 1 + γ − 1 2 M 2 ) T T ∗ = 1 ( 2 γ + 1 ) ( 1 + γ − 1 2 M 2 ) V V ∗ = M 1 ( 2 γ + 1 ) ( 1 + γ − 1 2 M 2 ) p 0 p 0 ∗ = 1 M [ ( 2 γ + 1 ) ( 1 + γ − 1 2 M 2 ) ] γ + 1 2 ( γ − 1 ) {\displaystyle {\begin{aligned}{\frac {p}{p^{*}}}&={\frac {1}{M}}{\frac {1}{\sqrt {\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)}}}\\{\frac {\rho }{\rho ^{*}}}&={\frac {1}{M}}{\sqrt {\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)}}\\{\frac {T}{T^{*}}}&={\frac {1}{\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)}}\\{\frac {V}{V^{*}}}&=M{\frac {1}{\sqrt {\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)}}}\\{\frac {p_{0}}{p_{0}^{*}}}&={\frac {1}{M}}\left[\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)\right]^{\frac {\gamma +1}{2\left(\gamma -1\right)}}\end{aligned}}}

アプリケーション

図3定面積ダクトに通じる超音速ノズルを示す。初期条件は点1にある。点2はノズルスロートにあり、M  = 1である。点3は等エントロピー流れからファノ流れへの遷移を示す。点4と点5は衝撃波発生前と衝撃波発生後の状態を示し、点Eはダクトの出口である。
図4図3の条件におけるH - S線図。等エントロピー流れではエントロピーは一定であるため、点1の状態は垂直に点3まで下降する。次に、流れはファンノ線に沿って進み、衝撃波によって流れが超音速から亜音速に変化するまで続く。その後、流れは再びファンノ線に沿って進み、ダクトを出る直前にほぼチョーク状態に達する。
図 5ファノ線とレイリー線の交差チャート。

ファンノ流れモデルは、ノズルの設計と解析でよく使用されます。ノズルでは、収束領域または拡大領域は等エントロピー流れでモデル化され、その後の定面積セクションはファンノ流れでモデル化されます。図 3 と 4 に示すように、ポイント 1 の上流条件が与えられている場合は、計算を行ってノズル出口マッハ数と定面積ダクト内の通常の衝撃波の位置を決定することができます。ポイント 2 はノズルのスロートを示しており、流れが詰まっている場合はM  = 1 になります。ポイント 3 は、流れが等エントロピーからファンノに遷移するノズルの端部を示しています。初期圧力が十分に高ければ、ブローダウン型超音速風洞の望ましい性能と同様に、定面積ダクトを通して超音速流れを維持できます。ただし、これらの図は、衝撃波がダクトを完全に移動する前を示しています。衝撃波が存在する場合、流れはファノ線の超音速部分から亜音速部分に移行し、その後M  = 1 に向かって進みます。図 4 の動きは、熱力学の第二法則を満たすために常に左から右への動きになります。

ファノ流れモデルは、レイリー流れモデルと広く併用されています。これらの2つのモデルは、エンタルピー-エントロピー線図とマッハ数-エントロピー線図上の点で交差しており、多くの用途で意味を持ちます。しかし、各モデルのエントロピー値は音速状態では等しくありません。各モデルにおいて、 M  = 1 でのエントロピー変化は0ですが、前述の記述は、同じ任意の点から音速点までのエントロピー変化がファノ流れモデルとレイリー流れモデルで異なることを意味します。s iとM iの初期値を定義すれば、各モデルに対して無次元エントロピーとマッハ数の関係を表す新しい方程式を定義できます。これらの方程式は、それぞれファノ流れとレイリー流れについて以下に示します。

Δ S F = s − s i c p = ln ⁡ [ ( M M i ) γ − 1 γ ( 1 + γ − 1 2 M i 2 1 + γ − 1 2 M 2 ) γ + 1 2 γ ] Δ S R = s − s i c p = ln ⁡ [ ( M M i ) 2 ( 1 + γ M i 2 1 + γ M 2 ) γ + 1 γ ] {\displaystyle {\begin{aligned}\Delta S_{F}&={\frac {s-s_{i}}{c_{p}}}=\ln \left[\left({\frac {M}{M_{i}}}\right)^{\frac {\gamma -1}{\gamma }}\left({\frac {1+{\frac {\gamma -1}{2}}M_{i}^{2}}{1+{\frac {\gamma -1}{2}}M^{2}}}\right)^{\frac {\gamma +1}{2\gamma }}\right]\\\Delta S_{R}&={\frac {s-s_{i}}{c_{p}}}=\ln \left[\left({\frac {M}{M_{i}}}\right)^{2}\left({\frac {1+\gamma M_{i}^{2}}{1+\gamma M^{2}}}\right)^{\frac {\gamma +1}{\gamma }}\right]\end{aligned}}}

図 5 は、 s i  = 0 およびM i = 3の初期条件で、ファノ線とレイリー線が交差している様子を示しています。 交点は、新しい無次元エントロピー方程式を互いに等しくすることで計算され、以下の関係が得られます。

  ( 1 + γ − 1 2 M i 2 ) [ M i 2 ( 1 + γ M i 2 ) 2 ] = ( 1 + γ − 1 2 M 2 ) [ M 2 ( 1 + γ M 2 ) 2 ] {\displaystyle \ \left(1+{\frac {\gamma -1}{2}}M_{i}^{2}\right)\left[{\frac {M_{i}^{2}}{\left(1+\gamma M_{i}^{2}\right)^{2}}}\right]=\left(1+{\frac {\gamma -1}{2}}M^{2}\right)\left[{\frac {M^{2}}{\left(1+\gamma M^{2}\right)^{2}}}\right]}

交点は、与えられた初期マッハ数とその法線後衝撃波値において発生します。図5では、これらの値はM  = 3と0.4752であり、ほとんどの圧縮性流れの教科書に記載されている法線衝撃波表に記載されています。ダクト面積が一定の流れの場合、これらの点でファノモデルとレイリーモデルが切り替わります。

参照

参考文献

  1. ^ Shapiro, AH、「圧縮性流体のダイナミクスと熱力学」第1巻、ロナルドプレス、1953年。
  2. ^ Zucker, RD, Biblarz, O.,気体力学の基礎、John Wiley & Sons、2002年。
  3. ^ Hodge, BK、Koenig, K.、「圧縮性流体力学とパーソナルコンピュータアプリケーション」、Prentice Hall、1995 年。
  4. ^ 流体運動の現象、RS Brodkey、p187、RS Brodkey（出版）、1995年
  • パーデュー大学の断熱および等温ファノフロー計算機
  • ケンタッキー大学 ファノフロー Web計算機
  • モーリス・W・ダウニー、ジーノ・ファノ
Retrieved from "https://en.wikipedia.org/w/index.php?title=Fanno_flow&oldid=1302584352"