デジタル信号処理におけるモデル
1 次ホールド ( FOH ) は、従来の デジタル アナログ コンバータ (DAC) と 積分器と 呼ばれる アナログ回路 で実行できる、サンプリングされた信号の実際的な再構成の数学的モデルです 。FOH では、信号はサンプリングされた元の信号に対する 区分線形 近似として再構成されます。FOH (または、より一般的には ゼロ次ホールド ) などの数学的モデルが必要なのは、 サンプリングおよび再構成定理において、離散サンプル x ( nT ) を表す ディラック インパルス のシーケンス x s ( t ) を ローパス フィルタ処理し て 、サンプリングされた元の信号 x ( t ) を復元するためです。ただし、ディラック インパルスのシーケンスを出力することは実際的ではありません。従来の DAC と何らかの線形アナログ回路を使用してデバイスを実装し、予測 FOH または遅延 FOH のいずれかの区分線形出力を再構成することができます。
これは物理的に行われることでは ありません が、仮想的なディラック インパルスのシーケンス x s ( t ) を 線形時間不変システム に適用することで、同一の出力を生成することができます。線形時間不変システムは、 そのような特性 (LTI システムの場合、 インパルス応答によって完全に記述されます) を持つ 線形フィルタ とも呼ばれ、各入力インパルスが出力で正しい区分線形関数になります。
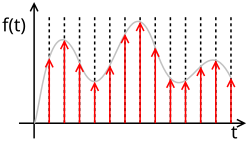
基本的な一次ホールド 理想的にサンプリングされた信号 x s ( t )。 一次ホールドは、 理想的にサンプリングされた信号を変換する
仮想 フィルタ または LTIシステムである。
×
s
( t )
{\displaystyle x_{s}(t)\,}
= × ( t )
T
∑
n = − ∞
∞
δ ( t − n T )
{\displaystyle =x(t)\ T\sum _{n=-\infty }^{\infty }\delta (t-nT)\ }
= T
∑
n = − ∞
∞
× ( n T ) δ ( t − n T )
{\displaystyle =T\sum _{n=-\infty }^{\infty }x(nT)\delta (t-nT)\ }
区分線形信号 x FOH ( t )。 区分線形信号に
×
F お H
( t ) =
∑
n = − ∞
∞
× ( n T )
t r 私
(
t − n T
T
)
{\displaystyle x_{\mathrm {FOH} }(t)\,=\sum _{n=-\infty }^{\infty }x(nT)\mathrm {tri} \left({\frac {t-nT}{T}}\right)\ }
一次ホールド h FOH ( t )のインパルス応答(非因果的)。 その結果、有効な インパルス応答 は
h
F お H
( t ) =
1 T
t r 私
(
t T
)
=
{
1 T
(
1 −
|
t
|
T
)
もし
|
t
|
< T
0
さもないと
{\displaystyle h_{\mathrm {FOH} }(t)\,={\frac {1}{T}}\mathrm {tri} \left({\frac {t}{T}}\right)={\begin{cases}{\frac {1}{T}}\left(1-{\frac {|t|}{T}}\right)&{\mbox{if }}|t|<T\\0&{\mbox{otherwise}}\end{cases}}\ }
ここで 、 は 三角関数 です。
t
r
i
(
x
)
{\displaystyle \mathrm {tri} (x)\ }
有効周波数応答は、 インパルス応答の
連続フーリエ変換です。
H
F
O
H
(
f
)
{\displaystyle H_{\mathrm {FOH} }(f)\,}
=
F
{
h
F
O
H
(
t
)
}
{\displaystyle ={\mathcal {F}}\{h_{\mathrm {FOH} }(t)\}\ }
=
(
e
i
π
f
T
−
e
−
i
π
f
T
i
2
π
f
T
)
2
{\displaystyle =\left({\frac {e^{i\pi fT}-e^{-i\pi fT}}{i2\pi fT}}\right)^{2}\ }
=
s
i
n
c
2
(
f
T
)
{\displaystyle =\mathrm {sinc} ^{2}(fT)\ }
ここで、正規化された sinc関数 です 。
s
i
n
c
(
x
)
=
sin
(
π
x
)
π
x
{\displaystyle \mathrm {sinc} (x)={\frac {\sin(\pi x)}{\pi x}}\ }
FOHの ラプラス 変換 伝達関数は、 s = i 2 π f を代入することによって求められます。
H
F
O
H
(
s
)
{\displaystyle H_{\mathrm {FOH} }(s)\,}
=
L
{
h
F
O
H
(
t
)
}
{\displaystyle ={\mathcal {L}}\{h_{\mathrm {FOH} }(t)\}\ }
=
(
e
s
T
/
2
−
e
−
s
T
/
2
s
T
)
2
{\displaystyle =\left({\frac {e^{sT/2}-e^{-sT/2}}{sT}}\right)^{2}\ }
これは、 線形補間関数が、仮想 FOH フィルターにサンプルが適用される前に、次のサンプルの値に向かって移動するという点で、
非因果的なシステムです。
遅延一次ホールド 遅延された区分線形信号 x FOH ( t )。 遅延一次ホールド (因果一次ホールド とも呼ばれる)は、 出力が1 サンプル周期 遅延され、遅延した区分線形出力信号が得られる点
を除いて、上記のFOHと同一である。
x
F
O
H
(
t
)
=
∑
n
=
−
∞
∞
x
(
n
T
)
t
r
i
(
t
−
T
−
n
T
T
)
{\displaystyle x_{\mathrm {FOH} }(t)\,=\sum _{n=-\infty }^{\infty }x(nT)\mathrm {tri} \left({\frac {t-T-nT}{T}}\right)\ }
因果的一次ホールド h FOH ( t )のインパルス応答。 その結果、有効な インパルス応答 は
h
F
O
H
(
t
)
=
1
T
t
r
i
(
t
−
T
T
)
=
{
1
T
(
1
−
|
t
−
T
|
T
)
if
|
t
−
T
|
<
T
0
otherwise
{\displaystyle h_{\mathrm {FOH} }(t)\,={\frac {1}{T}}\mathrm {tri} \left({\frac {t-T}{T}}\right)={\begin{cases}{\frac {1}{T}}\left(1-{\frac {|t-T|}{T}}\right)&{\mbox{if }}|t-T|<T\\0&{\mbox{otherwise}}\end{cases}}\ }
ここで 、 は 三角関数 です。
t
r
i
(
x
)
{\displaystyle \mathrm {tri} (x)\ }
有効周波数応答は、 インパルス応答の
連続フーリエ変換です。
H
F
O
H
(
f
)
{\displaystyle H_{\mathrm {FOH} }(f)\,}
=
F
{
h
F
O
H
(
t
)
}
{\displaystyle ={\mathcal {F}}\{h_{\mathrm {FOH} }(t)\}\ }
=
(
1
−
e
−
i
2
π
f
T
i
2
π
f
T
)
2
{\displaystyle =\left({\frac {1-e^{-i2\pi fT}}{i2\pi fT}}\right)^{2}\ }
=
e
−
i
2
π
f
T
s
i
n
c
2
(
f
T
)
{\displaystyle =e^{-i2\pi fT}\mathrm {sinc} ^{2}(fT)\ }
ここでは sinc 関数 です 。
s
i
n
c
(
x
)
{\displaystyle \mathrm {sinc} (x)\ }
遅延FOHの ラプラス 変換 伝達関数は、 s = i 2 π f を代入することによって求められます。
H
F
O
H
(
s
)
{\displaystyle H_{\mathrm {FOH} }(s)\,}
=
L
{
h
F
O
H
(
t
)
}
{\displaystyle ={\mathcal {L}}\{h_{\mathrm {FOH} }(t)\}\ }
=
(
1
−
e
−
s
T
s
T
)
2
{\displaystyle =\left({\frac {1-e^{-sT}}{sT}}\right)^{2}\ }
遅延出力により、これは 因果関係のあるシステム となります。遅延FOHのインパルス応答は、入力インパルスより前には応答しません。
この種の遅延区分線形再構成は、 ゲイン H ( z ) = 1 − z −1の デジタルフィルタ を実装し、そのデジタルフィルタの出力(単純に x [ n ]− x [ n −1])を理想的な従来の デジタル-アナログコンバータ (モデルとして固有の ゼロ次ホールドを 持つ)に適用し、DAC出力を積分(連続時間で、 H ( s ) = 1/( sT ))することで物理的に実現できます。
予測的な一次ホールド 予測FOH出力信号 xFOH ( t ) 。 最後に、 予測的一次ホールド は全く異なります。これは、 理想的にサンプリングされた信号を変換する
因果的な仮説的LTIシステムまたはフィルタです。
x
s
(
t
)
{\displaystyle x_{s}(t)\,}
=
x
(
t
)
T
∑
n
=
−
∞
∞
δ
(
t
−
n
T
)
{\displaystyle =x(t)\ T\sum _{n=-\infty }^{\infty }\delta (t-nT)\ }
=
T
∑
n
=
−
∞
∞
x
(
n
T
)
δ
(
t
−
n
T
)
{\displaystyle =T\sum _{n=-\infty }^{\infty }x(nT)\delta (t-nT)\ }
現在のサンプルと直前のサンプルを用いて 次のサンプリング点まで
線形外挿する、区分線形出力に 変換する。このようなフィルタの出力は次のようになる。
x
F
O
H
(
t
)
{\displaystyle x_{\mathrm {FOH} }(t)\,}
=
∑
n
=
−
∞
∞
(
x
(
n
T
)
+
(
x
(
n
T
)
−
x
(
(
n
−
1
)
T
)
)
t
−
n
T
T
)
r
e
c
t
(
t
−
n
T
T
−
1
2
)
{\displaystyle =\sum _{n=-\infty }^{\infty }\left(x(nT)+\left(x(nT)-x((n-1)T)\right){\frac {t-nT}{T}}\right)\mathrm {rect} \left({\frac {t-nT}{T}}-{\frac {1}{2}}\right)\ }
=
∑
n
=
−
∞
∞
x
(
n
T
)
(
r
e
c
t
(
t
−
n
T
T
−
1
2
)
−
r
e
c
t
(
t
−
n
T
T
−
3
2
)
+
t
r
i
(
t
−
n
T
T
−
1
)
)
{\displaystyle =\sum _{n=-\infty }^{\infty }x(nT)\left(\mathrm {rect} \left({\frac {t-nT}{T}}-{\frac {1}{2}}\right)-\mathrm {rect} \left({\frac {t-nT}{T}}-{\frac {3}{2}}\right)+\mathrm {tri} \left({\frac {t-nT}{T}}-1\right)\right)\ }
予測一次ホールド h FOH ( t )のインパルス応答。 その結果、有効な インパルス応答 は
h
F
O
H
(
t
)
{\displaystyle h_{\mathrm {FOH} }(t)\,}
=
1
T
(
r
e
c
t
(
t
T
−
1
2
)
−
r
e
c
t
(
t
T
−
3
2
)
+
t
r
i
(
t
T
−
1
)
)
{\displaystyle ={\frac {1}{T}}\left(\mathrm {rect} \left({\frac {t}{T}}-{\frac {1}{2}}\right)-\mathrm {rect} \left({\frac {t}{T}}-{\frac {3}{2}}\right)+\mathrm {tri} \left({\frac {t}{T}}-1\right)\right)\ }
=
{
1
T
(
1
+
t
T
)
if
0
≤
t
<
T
1
T
(
1
−
t
T
)
if
T
≤
t
<
2
T
0
otherwise
{\displaystyle ={\begin{cases}{\frac {1}{T}}\left(1+{\frac {t}{T}}\right)&{\mbox{if }}0\leq t<T\\{\frac {1}{T}}\left(1-{\frac {t}{T}}\right)&{\mbox{if }}T\leq t<2T\\0&{\mbox{otherwise}}\end{cases}}\ }
ここで は 長方形関数 、は 三角関数 です 。
r
e
c
t
(
x
)
{\displaystyle \mathrm {rect} (x)\ }
t
r
i
(
x
)
{\displaystyle \mathrm {tri} (x)\ }
有効周波数応答は、 インパルス応答の
連続フーリエ変換です。
H
F
O
H
(
f
)
{\displaystyle H_{\mathrm {FOH} }(f)\,}
=
F
{
h
F
O
H
(
t
)
}
{\displaystyle ={\mathcal {F}}\{h_{\mathrm {FOH} }(t)\}\ }
=
(
1
+
i
2
π
f
T
)
(
1
−
e
−
i
2
π
f
T
i
2
π
f
T
)
2
{\displaystyle =(1+i2\pi fT)\left({\frac {1-e^{-i2\pi fT}}{i2\pi fT}}\right)^{2}\ }
=
(
1
+
i
2
π
f
T
)
e
−
i
2
π
f
T
s
i
n
c
2
(
f
T
)
)
{\displaystyle =(1+i2\pi fT)e^{-i2\pi fT}\mathrm {sinc} ^{2}(fT))\ }
ここでは sinc 関数 です 。
s
i
n
c
(
x
)
{\displaystyle \mathrm {sinc} (x)\ }
予測FOHの ラプラス 変換 伝達関数は、 s = i 2 π f を代入することによって求められます。
H
F
O
H
(
s
)
{\displaystyle H_{\mathrm {FOH} }(s)\,}
=
L
{
h
F
O
H
(
t
)
}
{\displaystyle ={\mathcal {L}}\{h_{\mathrm {FOH} }(t)\}\ }
=
(
1
+
s
T
)
(
1
−
e
−
s
T
s
T
)
2
{\displaystyle =(1+sT)\left({\frac {1-e^{-sT}}{sT}}\right)^{2}\ }
これは 因果的なシステム です。予測型FOHのインパルス応答は、入力インパルスより前には応答しません。
この種の区分線形再構成は、 ゲイン H ( z ) = 1 − z −1の デジタルフィルタ を実装し、そのデジタルフィルタの出力(単純に x [ n ]− x [ n −1])を理想的な従来の デジタル/アナログコンバータ (モデルとして固有の ゼロ次ホールドを持つ)に適用し、その DAC 出力を伝達関数 H ( s ) = (1+ sT )/( sT )を持つアナログフィルタに適用することによって物理的に実現できます 。
参照
外部リンク Sankar, Krishna (2007). 「ゼロ次ホールドと一次ホールドに基づく補間」 dspLog 通信用信号処理 .