ガウス法

軌道力学（天体力学の一分野）において、ガウス法は、対象とする軌道天体の3つの異なる時刻における少なくとも3回の観測（観測回数が多いほど、決定された軌道の精度が向上する）に基づいて、予備的な軌道決定を行うために用いられる。必要な情報は、観測時刻、観測点の位置ベクトル（赤道座標系）、観測点からの軌道天体の方向余弦ベクトル（トポセントリック赤道座標系）、および一般的な物理データである。

1801年、カール・フリードリヒ・ガウスは、ケレスの軌道を決定するために特に用いられた重要な数学的手法（ガウス法にまとめられている）を開発しました。以下に示す方法は、観測が行われた中心天体の周りを周回する天体の軌道を決定するものですが、ケレスの軌道を決定する方法は、ケレスが太陽を周回する間に地球から観測を行うため、より複雑な手順を要します。

観測者の位置ベクトル

観測点の観測者位置ベクトル（赤道座標系）は、次のいずれかの方法で、軌道を周回する天体（たとえば地球）の焦点天体の表面の緯度と現地恒星時（地心座標系）から決定できます。

$${\displaystyle {\begin{aligned}\mathbf {R_{n}} &=\left[{R_{e} \over {\sqrt {1-(2f-f^{2})\sin ^{2}\phi _{n}}}}+H_{n}\right]\cos \phi _{n}(\cos \theta _{n}\ \mathbf {\hat {I}} +\sin \theta _{n}\ \mathbf {\hat {J}} )+\left[{R_{e}(1-f)^{2} \over {\sqrt {1-(2f-f^{2})\sin ^{2}\phi _{n}}}}+H_{n}\right]\sin \phi _{n}\ \mathbf {\hat {K}} \\&=\left[{R_{e} \over {\sqrt {1-e^{2}\sin ^{2}\phi _{n}}}}+H_{n}\right]\cos \phi _{n}(\cos \theta _{n}\ \mathbf {\hat {I}} +\sin \theta _{n}\ \mathbf {\hat {J}} )+\left[{R_{e}(1-e^{2}) \over {\sqrt {1-e^{2}\sin ^{2}\phi _{n}}}}+H_{n}\right]\sin \phi _{n}\ \mathbf {\hat {K}} \end{aligned}}}$$ または 、 $${\displaystyle \mathbf {R_{n}} =r_{e}\cos \phi '_{n}\cos \theta _{n}\ \mathbf {\hat {I}} +r_{e}\cos \phi '_{n}\sin \theta _{n}\ \mathbf {\hat {J}} +r_{e}\sin \phi '_{n}\ \mathbf {\hat {K}} }$$

• ${\displaystyle \mathbf {R_{n}} }$ それぞれの観測者の位置ベクトル（赤道座標系）
• ${\displaystyle R_{e}}$ 中心天体の赤道半径（例えば地球の場合は6,378 km）
• ${\displaystyle r_{e}}$ 地心距離
• ${\displaystyle f}$ 中心天体の扁平率（または平坦度）（例えば地球の場合は0.003353）
• ${\displaystyle e}$ 中心天体の離心率（例えば地球の場合は0.081819）
• ${\displaystyle \phi _{n}}$ 測地緯度（水平面の法線と赤道面の間の角度）
• ${\displaystyle \phi '_{n}}$ 地心緯度（半径と赤道面の間の角度）
• ${\displaystyle H_{n}}$ 測地高度は
• ${\displaystyle \theta _{n}}$ 観測地点の現地恒星時

軌道物体の方向余弦ベクトル

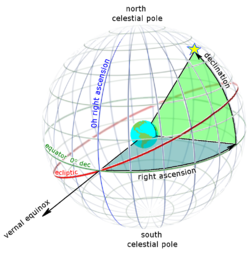
天球の外から見た赤経（青）と赤緯（緑）

軌道物体の方向余弦ベクトルは、観測点からの軌道物体の 赤経と赤緯（地心赤道座標系から）から次のように決定できます。

$${\displaystyle \mathbf {{\hat {\boldsymbol {\rho }}}_{n}} =\cos \delta _{n}\cos \alpha _{n}\ \mathbf {\hat {I}} +\cos \delta _{n}\sin \alpha _{n}\ \mathbf {\hat {J}} +\sin \delta _{n}\ \mathbf {\hat {K}} }$$ ここで、

• ${\displaystyle \mathbf {{\hat {\boldsymbol {\rho }}}_{n}} }$ は位置ベクトルの方向のそれぞれの単位ベクトルです（地心赤道座標系における観測点から周回天体への方向）。${\displaystyle \rho }$
• ${\displaystyle \delta _{n}}$ それぞれの偏角
• ${\displaystyle \alpha _{n}}$ それぞれの赤経

アルゴリズム

最初の導出は、軌道を周回する物体の位置ベクトルを決定するためのベクトル加算から始まります。次に、角運動量保存則とケプラーの軌道原理（軌道は3次元空間内の2次元平面にあると述べている）に基づいて、これらの位置ベクトルの線形結合が確立されます。また、物体の位置と速度ベクトルの関係をラグランジュ係数によって表し、その結果、これらの係数が使用されるようになります。次に、ベクトル操作と代数を用いて、以下の式が導出されます。詳細な導出については、Curtisを参照してください。^[1]

注：ガウス法は、あくまでも予備的な軌道決定法であり、その重要性は強調されています。ラグランジュ係数の近似値と、必要な観測条件の制限（例えば、観測間の弧の曲率が小さいこと。詳細はグロンキ^{[2]を参照）により、不正確な結果が生じます。しかし、ガウス法は、}ケプラー方程式を解くなど、サブコンポーネントの精度を向上させることで改善できます。精度を向上させるもう一つの方法は、観測回数を増やすことです。

ステップ1

時間間隔を計算し、観測間の時間を減算します。 ここで $${\displaystyle {\begin{aligned}\tau _{1}&=t_{1}-t_{2}\\\tau _{3}&=t_{3}-t_{2}\\\tau &=t_{3}-t_{1}\end{aligned}}}$$

• ${\displaystyle \tau _{n}}$ 時間間隔は
• ${\displaystyle t_{n}}$ それぞれの観測時間

ステップ2

右手座標系に関する外積

外積を計算し、観測単位方向の外積を求める（順序は重要）： ここで $${\displaystyle {\begin{aligned}\mathbf {p_{1}} &=\mathbf {{\hat {\boldsymbol {\rho }}}_{2}} \times \mathbf {{\hat {\boldsymbol {\rho }}}_{3}} \\\mathbf {p_{2}} &=\mathbf {{\hat {\boldsymbol {\rho }}}_{1}} \times \mathbf {{\hat {\boldsymbol {\rho }}}_{3}} \\\mathbf {p_{3}} &=\mathbf {{\hat {\boldsymbol {\rho }}}_{1}} \times \mathbf {{\hat {\boldsymbol {\rho }}}_{2}} \end{aligned}}}$$

• ${\displaystyle \mathbf {a} \times \mathbf {b} }$ ベクトルの外積である${\displaystyle \mathbf {a} {\text{ and }}\mathbf {b} }$
• ${\displaystyle \mathbf {p_{n}} }$ はそれぞれの外積ベクトルである
• ${\displaystyle \mathbf {{\hat {\boldsymbol {\rho }}}_{n}} }$ それぞれの単位ベクトル

ステップ3

平行六面体を定義する3つのベクトル。三重積の大きさは体積を表します${\displaystyle |\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|}$

共通スカラー量（スカラー三重積）を計算し、最初の観測単位ベクトルのドット積と、2番目と3番目の観測単位ベクトルの外積をとります。

$${\displaystyle D_{0}=\mathbf {{\hat {\boldsymbol {\rho }}}_{1}} \cdot \mathbf {p_{1}} =\mathbf {{\hat {\boldsymbol {\rho }}}_{1}} \cdot (\mathbf {{\hat {\boldsymbol {\rho }}}_{2}} \times \mathbf {{\hat {\boldsymbol {\rho }}}_{3}} )}$$ ここで

• ${\displaystyle \mathbf {a} \cdot \mathbf {b} }$ はベクトルの内積であり、${\displaystyle \mathbf {a} }$ ${\displaystyle \mathbf {b} }$
• ${\displaystyle D_{0}}$ は一般的なスカラー三重積である
• ${\displaystyle \mathbf {p_{n}} }$ はそれぞれの外積ベクトルである
• ${\displaystyle \mathbf {{\hat {\boldsymbol {\rho }}}_{n}} }$ それぞれの単位ベクトル

ステップ4

9つのスカラー量を計算します（ステップ3と同様）。 ここで $${\displaystyle {\begin{aligned}D_{11}&=\mathbf {R_{1}} \cdot \mathbf {p_{1}} &D_{12}&=\mathbf {R_{1}} \cdot \mathbf {p_{2}} &D_{13}&=\mathbf {R_{1}} \cdot \mathbf {p_{3}} \\D_{21}&=\mathbf {R_{2}} \cdot \mathbf {p_{1}} &D_{22}&=\mathbf {R_{2}} \cdot \mathbf {p_{2}} &D_{23}&=\mathbf {R_{2}} \cdot \mathbf {p_{3}} \\D_{31}&=\mathbf {R_{3}} \cdot \mathbf {p_{1}} &D_{32}&=\mathbf {R_{3}} \cdot \mathbf {p_{2}} &D_{33}&=\mathbf {R_{3}} \cdot \mathbf {p_{3}} \end{aligned}}}$$

• ${\displaystyle D_{mn}}$ それぞれのスカラー量である
• ${\displaystyle \mathbf {R_{m}} }$ それぞれの観測者の位置ベクトル
• ${\displaystyle \mathbf {p_{n}} }$ はそれぞれの外積ベクトルである

ステップ5

スカラー位置係数を計算します。

$${\displaystyle {\begin{aligned}A&={\frac {1}{D_{0}}}\left(-D_{12}{\frac {\tau _{3}}{\tau }}+D_{22}+D_{32}{\frac {\tau _{1}}{\tau }}\right)\\B&={\frac {1}{6D_{0}}}\left[D_{12}\left(\tau _{3}^{2}-\tau ^{2}\right){\frac {\tau _{3}}{\tau }}+D_{32}\left(\tau ^{2}-\tau _{1}^{2}\right){\frac {\tau _{1}}{\tau }}\right]\\E&=\mathbf {R_{2}} \cdot \mathbf {{\hat {\boldsymbol {\rho }}}_{2}} \end{aligned}}}$$ ここで

• ${\displaystyle A}$ 、、はスカラー位置係数です${\displaystyle B}$ ${\displaystyle E}$
• ${\displaystyle D_{0}}$ 共通のスカラー量である
• ${\displaystyle D_{mn}}$ それぞれのスカラー量
• ${\displaystyle \tau _{n}}$ 時間間隔は
• ${\displaystyle R_{n}}$ それぞれの観測者の位置ベクトル
• ${\displaystyle \mathbf {{\hat {\boldsymbol {\rho }}}_{n}} }$ それぞれの単位ベクトル

ステップ6

2番目の観測値の位置ベクトルのドット積をとって、2番目の観測値の2乗スカラー距離を計算します。 ここで $${\displaystyle {R_{2}}^{2}=\mathbf {R_{2}} \cdot \mathbf {R_{2}} }$$

• ${\displaystyle {R_{2}}^{2}}$ 2番目の観測値の二乗距離である
• ${\displaystyle \mathbf {R_{2}} }$ 2番目の観測点の位置ベクトルである

ステップ7

軌道上の天体の2回目の観測におけるスカラー距離多項式の係数を計算します。 ここで $${\displaystyle {\begin{aligned}a&=-\left(A^{2}+2AE+{R_{2}}^{2}\right)\\b&=-2\mu B(A+E)\\c&=-\mu ^{2}B^{2}\end{aligned}}}$$

• ${\displaystyle a{\text{, }}b{\text{, and }}c}$ 軌道上の天体の2回目の観測におけるスカラー距離多項式の係数である。
• ${\displaystyle A{\text{, }}B{\text{, and }}E}$ スカラー位置係数である
• ${\displaystyle \mu }$ 軌道を周回する天体の焦点天体の重力パラメータである

ステップ8

軌道上の天体の2回目の観測におけるスカラー距離多項式の根を求めます。 ここで $${\displaystyle {r_{2}}^{8}+a{r_{2}}^{6}+b{r_{2}}^{3}+c=0}$$

• ${\displaystyle r_{2}}$ は、軌道を周回する天体の2回目の観測のスカラー距離である（それとそのベクトルr ₂は赤道座標系にある）
• ${\displaystyle a{\text{, }}b{\text{, and }}c}$ 前述の通り係数である

根を求めるには様々な方法がありますが、ニュートン・ラプソン法が推奨されます。根は物理的に可能な値（つまり、負数や複素数ではない値）でなければなりません。複数の根が考えられる場合は、それぞれを評価し、利用可能なデータと比較することで、その妥当性を確認する必要があります。

ステップ9

それぞれの時刻における観測点から周回天体までの距離である 斜距離を計算します。 ここで $${\displaystyle {\begin{aligned}\rho _{1}&={\frac {1}{D_{0}}}\left[{\frac {6\left(D_{31}{\dfrac {\tau _{1}}{\tau _{3}}}+D_{21}{\dfrac {\tau }{\tau _{3}}}\right){r_{2}}^{3}+\mu D_{31}\left(\tau ^{2}-{\tau _{1}}^{2}\right){\dfrac {\tau _{1}}{\tau _{3}}}}{6{r_{2}}^{3}+\mu \left(\tau ^{2}-{\tau _{3}}^{2}\right)}}-D_{11}\right]\\\rho _{2}&=A+{\frac {\mu B}{{r_{2}}^{3}}}\\\rho _{3}&={\frac {1}{D_{0}}}\left[{\frac {6\left(D_{13}{\dfrac {\tau _{3}}{\tau _{1}}}-D_{23}{\dfrac {\tau }{\tau _{1}}}\right){r_{2}}^{3}+\mu D_{13}\left(\tau ^{2}-{\tau _{3}}^{2}\right){\dfrac {\tau _{3}}{\tau _{1}}}}{6{r_{2}}^{3}+\mu \left(\tau ^{2}-{\tau _{1}}^{2}\right)}}-D_{33}\right]\end{aligned}}}$$

• ${\displaystyle \rho _{n}}$ はそれぞれの斜距離である（それとそのベクトルは地心赤道座標系にある）${\displaystyle \mathbf {\rho _{n}} }$
• ${\displaystyle D_{0}}$ 共通のスカラー量である
• ${\displaystyle D_{mn}}$ それぞれのスカラー量
• ${\displaystyle \tau _{(n)}}$ 時間間隔です。
• ${\displaystyle r_{2}}$ 軌道上の天体の2回目の観測のスカラー距離である。
• ${\displaystyle \mu }$ 軌道を周回する天体の焦点天体の重力パラメータである

ステップ10

観測者の位置ベクトルと傾斜方向ベクトル（傾斜距離と傾斜方向ベクトルの積）を加算して、周回天体の位置ベクトルを計算します

$${\displaystyle {\begin{aligned}\mathbf {r_{1}} &=\mathbf {R_{1}} +\rho _{1}\mathbf {{\hat {\boldsymbol {\rho }}}_{1}} \\[1.7ex]\mathbf {r_{2}} &=\mathbf {R_{2}} +\rho _{2}\mathbf {{\hat {\boldsymbol {\rho }}}_{2}} \\[1.7ex]\mathbf {r_{3}} &=\mathbf {R_{3}} +\rho _{3}\mathbf {{\hat {\boldsymbol {\rho }}}_{3}} \end{aligned}}}$$ ここで

• ${\displaystyle \mathbf {r_{n}} }$ はそれぞれの軌道上の天体の位置ベクトル（赤道座標系）です
• ${\displaystyle \mathbf {R_{n}} }$ それぞれの観測者の位置ベクトル
• ${\displaystyle \rho _{n}}$ それぞれの斜距離
• ${\displaystyle \mathbf {{\hat {\boldsymbol {\rho }}}_{n}} }$ それぞれの単位ベクトル

ステップ11

ラグランジュ係数を計算します。 ここで、 $${\displaystyle {\begin{aligned}f_{1}&\approx 1-{\frac {1}{2}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{1}}^{2}\\f_{3}&\approx 1-{\frac {1}{2}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{3}}^{2}\\g_{1}&\approx \tau _{1}-{\frac {1}{6}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{1}}^{3}\\g_{3}&\approx \tau _{3}-{\frac {1}{6}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{3}}^{3}\end{aligned}}}$$

• ${\displaystyle f_{1}}$ 、、はラグランジュ係数です（これらは、短い時間間隔を仮定した級数式の最初の2項です）。${\displaystyle f_{3}}$ ${\displaystyle g_{1}}$ ${\displaystyle g_{3}}$
• ${\displaystyle \mu }$ 軌道を周回する天体の焦点天体の重力パラメータである
• ${\displaystyle r_{2}}$ 軌道上の天体の2回目の観測のスカラー距離である。
• ${\displaystyle \tau _{(n)}}$ 時間間隔は

ステップ12

軌道上の天体の2回目の観測の速度ベクトルを計算します

$${\displaystyle \mathbf {v_{2}} ={\frac {1}{f_{1}g_{3}-f_{3}g_{1}}}\left(-f_{3}\mathbf {r_{1}} +f_{1}\mathbf {r_{3}} \right)}$$ ここで

• ${\displaystyle \mathbf {v_{2}} }$ 軌道上の物体の2回目の観測の速度ベクトル（赤道座標系）
• ${\displaystyle f_{1}}$ 、、はラグランジュ係数である。${\displaystyle f_{3}}$ ${\displaystyle g_{1}}$ ${\displaystyle g_{3}}$
• ${\displaystyle \mathbf {r_{n}} }$ それぞれの軌道上の物体の位置ベクトル

ステップ13

軌道状態ベクトル、すなわち軌道を周回する天体の2回目の観測における位置ベクトル（ r ₂）と速度ベクトル（v ₂ ）が求められました。これらの2つのベクトルを用いて、軌道要素を求め、軌道を決定できます

参照

• 円周角定理と楕円の三点形式

参考文献

1. カーティス、ハワードD.『工学部学生のための軌道力学』オックスフォード：エルゼビア・バターワース・ハイネマン、2005年。印刷。
2. Gronchi, Giovanni F.. 「小惑星の古典的および現代的な軌道決定法」国際天文学連合紀要2004.IAUC196 (2004): 1-11. 印刷。

• Der, Gim J.. 「初期軌道決定のための新しい角度のみのアルゴリズム」Advanced Maui Optical and Space Surveillance Technologies Conference. (2012). 印刷