ジョセフソン効果

国立標準技術研究所が標準電圧として開発したジョセフソン接合アレイチップ

物理学において、ジョセフソン効果とは、2つの超伝導体が近接し、その間に何らかの障壁または制限がある場合に発生する現象です。この効果は、1962年に弱結合を流れる電流と電圧の数学的関係を予測したイギリスの物理学者ブライアン・ジョセフソンにちなんで名付けられました。 ^{[1] [2]}これは、量子力学の効果が原子スケールではなく通常のスケールで観測可能な、マクロな量子現象の一例です。ジョセフソン効果は、電圧や周波数などの異なる物理的測定値の間に正確な関係を示し、高精度な測定を可能にするため、多くの実用的応用があります。

ジョセフソン効果は、電圧を印加しなくてもジョセフソン接合（JJ）と呼ばれる装置を流れる電流（超電流）を発生させます。 ^{[説明が必要]}これは、2つ以上の超伝導体が弱い結合で結合した構造です。弱い結合とは、薄い絶縁体障壁（超伝導体-絶縁体-超伝導体接合、SIS）、非超伝導金属の短い部分（SNS）、または接触点における超伝導性を弱める物理的な狭窄（ScS）などです。

ジョセフソン接合は、 SQUID、超伝導量子ビット、RSFQデジタルエレクトロニクスなどの量子力学回路において重要な用途を持っています。NISTの1ボルト標準は、 20,208個のジョセフソン接合を直列に接続することで達成されます。^[3]

歴史

モンド研究所ビル^[4]

DCジョセフソン効果は1962年以前の実験でも確認されていたが^[5] 、絶縁障壁の「超短絡」または破壊によって超伝導体間で電子が直接伝導する現象に起因するものと考えられていた。

1962年、ブライアン・ジョセフソンは超伝導トンネル効果に興味を持つようになった。当時23歳で、ケンブリッジ大学モンド研究所でブライアン・ピパードの指導を受ける大学院2年生だった。同年、ジョセフソンはベル研究所の職員で1961年から1962年の学年度にサバティカル休暇を取っていたフィリップ・W・アンダーソンの多体理論の講義を受講した。この講義でジョセフソンは超伝導における対称性の破れという概念に触れ、「対称性の破れという概念に魅了され、実験的に観測する方法があるのではないかと考えた」という。ジョセフソンは、イヴァル・ジャーバーとハンス・マイスナーの実験、そしてロバート・パーメンターの理論的研究を研究した。ピパードは当初、トンネル効果はあり得るが、その効果は小さすぎて目立たないと考えていたが、ジョセフソンは同意しなかった。特にアンダーソンが、マーヴィン・L・コーエン、レオポルド・マキシモ・ファリコフ、ジェームズ・チャールズ・フィリップスによる超伝導体-障壁-常伝導金属系に関する「超伝導トンネル効果」のプレプリントをジョセフソンに紹介した後は、同意しなかった。^{[6] [7] : 223–224}

ジョセフソンとその同僚たちは当初、ジョセフソンの計算の妥当性に確信が持てなかった。アンダーソンは後にこう回想している。

ジョセフソン、ピパード、そして私、そしてモンドティーにいつも同席し、その後数週間の議論に参加した他のさまざまな人々も、電流が位相に依存するという事実の意味に非常に困惑していました。

更なる検討の後、彼らはジョセフソンの結果が妥当であると結論付けました。ジョセフソンは1962年6月に「超伝導トンネル効果における新たな効果の可能性」をPhysics Letters誌^{に投稿しました[1]}。より確立されたPhysical Review Letters誌ではなく、より新しい雑誌であるPhysics Letters誌が選ばれたのは、結果に不確実性があったためです。当時既にノーベル賞を受賞していたジョン・バーディーンは、1962年の当初はジョセフソンの理論に懐疑的な見解を示していましたが、その後の実験と理論的解明を経て、理論を受け入れるようになりました^{[7] 。222–227}参照：ジョン・バーディーン § ジョセフソン効果論争。

1963年1月、アンダーソンとベル研究所の同僚ジョン・ローウェルは、ジョセフソン効果の実験的観測を主張する最初の論文「ジョセフソン超伝導トンネル効果の推定的観測」をフィジカル・レビュー・レターズ誌に提出した。 ^{[8]両著者は、この効果に関する特許[9]}を取得したが、実際に行使されることはなかったものの、異議を唱えられることもなかった。^[要出典]

ジョセフソンの予言以前は、単一電子（すなわち非対電子）が量子トンネル効果によって絶縁障壁を通過できることしか知られていませんでした。ジョセフソンは超伝導クーパー対のトンネル効果を初めて予言しました。この功績により、ジョセフソンは1973年にノーベル物理学賞を受賞しました。 ^[10]バーディーンも推薦者の一人でした。^{[7] : 230}

ピパードの教え子でもあるジョン・クラークは、自身の研究はブライアン・ジョセフソンから多大な影響を受けたと述べている。^[11] 1985年、ミシェル・デボレとジョン・M・マルティニスを含むジョン・クラークのチームは、ジョセフソン接合を50 mK以下に冷却し、単一位相で記述されるマクロな量子挙動を実証した。 ^[12]マイクロ波パルスを使用して、彼らはゼロバイアスでエネルギーが量子化されることを実証した。^{[12]この発見は後に}超伝導キュービットの 開発に利用された。クラーク、デボレ、マルティニスは、この発見により2025年にノーベル物理学賞を受賞した。^[12]

アプリケーション

ジョセフソン接合の電気記号

ジョセフソン接合の種類には、φジョセフソン接合（πジョセフソン接合はその特殊な例）、長ジョセフソン接合、超伝導トンネル接合などがある。その他の用途としては、以下のものがある。

• 「デイエムブリッジ」は薄膜ジョセフソン接合であり、その弱結合部は数マイクロメートル以下の超伝導線で構成されている。^{[13] [14]}
• ジョセフソン接合数は超伝導電子回路の複雑さを表す代理変数である。
• SQUID（超伝導量子干渉素子）は、ジョセフソン効果を利用して動作する非常に感度の高い磁力計である。
• 超流動ヘリウム量子干渉素子（SHeQUID）は、DC-SQUIDの超流動ヘリウムアナログである^[15]
• 精密計測において、ジョセフソン効果は周波数と電圧間の再現性のある変換です。ジョセフソン電圧標準は、セシウム標準の周波数定義を採用し、電圧の標準表現を提供します。
• 単電子トランジスタは超伝導材料から作られることが多く、「超伝導単電子トランジスタ」と呼ばれる。^[16]
• 素電荷は、ジョセフソン定数と量子ホール効果に関連するフォン・クリッツィング定数によって最も正確に測定される。
• RSFQデジタルエレクトロニクスは、シャント接続されたジョセフソン接合に基づいています。接合のスイッチングにより1つの磁束量子 が放出されます。その存在と不在は、2進数の1と0を表します。${\displaystyle \scriptstyle {\frac {1}{2e}}h}$
• 超伝導量子コンピューティングでは、トランスモン量子ビットやフラックス量子ビットなどの量子ビット、あるいは位相と電荷が共役変数である他の方式において、ジョセフソン接合を非線形誘導素子として使用します。^[17]
• 超伝導トンネル接合検出器は超伝導カメラに使用されている

材料

ジョセフソン接合は、2つの超伝導電極に挟まれた障壁材料で構成され、この障壁は超伝導体間の弱結合として機能します。この弱結合は、その性質に応じて絶縁層、通常の金属、または狭い狭窄部となり、様々な種類のジョセフソン接合（SIS接合、SNS接合、または狭窄接合）が存在します。^[18]長年にわたり、特定の用途における接合性能を最適化するために、電極と障壁の両方に多様な材料が検討されてきました。ジョセフソン接合における材料選択は、誘電損失、構造的および化学的安定性、経年変化、超伝導転移温度、製造の容易さ、界面の均一性と粗さ、そして二準位系[TLS]の存在など、いくつかの要因によって決まります。研究されている多くの材料系の中で、アルミニウムベースのAl|AlOx|Al接合は、その再現性と低いマイクロ波損失により、多くの超伝導量子ビットアーキテクチャにおける最先端材料として浮上しています。 ^[19]

電極材料

電極材料の選択は、トランズモン量子ビット、SQUID、検出器などの用途と製造上の適合性に依存します。超伝導電極の重要な要件は、十分に高い超伝導転移温度です。この温度は超伝導エネルギーギャップを決定し、ジョセフソン接合の電流電圧特性に直接影響を及ぼします。アルミニウムは、その製造容易さと高品質を特徴とする天然酸化物バリアのため、最先端の量子ビットにおいて最も広く使用されている電極材料です。ニオブやタンタルもよく使用され、より高い転移温度と優れた堅牢性を提供します。また、ニオブ窒化物（NbN）などの材料は、特殊な高周波用途や検出器用途向けに、さらに高いTc値を提供します。

アルミニウム(Al)は、製造が容易で、高品質のトンネル障壁と互換性があるため、最先端の超伝導量子ビットで最も広く使用されている電極材料です。

ニオブ（Nb）も広く用いられており、純粋なNbは約9.3 Kの超伝導転移温度を示す。Nb/Al-AlOx/Nb接合は、多くの超伝導量子ビットや集積回路に用いられている。しかし、Nbは大気中の酸素に敏感で、容易に自然酸化物を形成するため、実効超伝導転移温度が低下する可能性がある。無秩序なNb薄膜では、Tc値が約5.7 Kであることが報告されている。 ^[20]

タンタル（Ta）は、低損失量子回路用の有望な電極材料として近年注目されています。超伝導α-Ta相の転移温度は約4.4 Kで、ジョセフソン接合や超伝導共振器においてNbと組み合わせて使用​​されています。一方、β-Ta相は1 K以下の温度でのみ超伝導状態となります。Ta膜の結晶相と電気特性は成長条件と基板の選択に大きく依存するため、堆積パラメータを慎重に制御する必要があります。 ^{[21] [22]}

窒化ニオブ（NbN）は、立方晶δ-NbN相で約17 Kに達する超伝導転移温度の高さから、ますます注目を集めています。NbN薄膜は、スパッタリングや分子線エピタキシーなどのいくつかの堆積技術を使用して成長しており、ナノメートルスケールの厚さで高Tc膜が報告されています。 ^{[23]しかし、NbNの}コヒーレンス長が短いため、ジョセフソン接合三層における界面の品質と均一性に厳しい要件が課せられます。窒化ニオブ（NbN）は、主に立方晶岩塩型（δ-NbN）および六方晶ウルツ鉱型関連構造で結晶化し、超伝導特性は結晶相に大きく依存します。立方晶系δ-NbN相は最も高い超伝導転移温度を示し、典型的には11～17 Kの範囲であるのに対し、六方晶系相はTc値が大幅に低く、1 K未満になることが多い。成長パラメータ、特に基板温度を制御することで立方晶系相を安定化させることができ、NbNは高Tcジョセフソン接合や超伝導デバイスに魅力的な材料となっている。 ^[24]

バリア材

ジョセフソン接合における障壁材料は、主に誘電損失を最小限に抑えつつ、再現性が高く制御性の高いトンネル界面を提供するために選択される。これらの層は通常数ナノメートルの厚さしかないため、構造の無秩序性と欠陥密度が接合性能に大きな影響を与える可能性があり、二準位系（TLS）が損失メカニズムを支配することが多い。トンネル電流は障壁の厚さに指数関数的に依存するため、障壁の厚さは特に重要である。^[25]

酸化アルミニウム（AlOx）は最先端の超伝導量子ビットで最も広く使用されているトンネル障壁であり、Al|AlOx|Alジョセフソン接合の基礎を形成しています。AlOxは、TLS関連の誘電損失と量子ビットのデコヒーレンスに寄与する酸素空孔を含むアモルファス酸化物として自然に成長します。^{[25]この制限にもかかわらず、AlOxはアルミニウム上での自己制限的な成長により支配的であり、1～2 nmの範囲で障壁の厚さを信頼性高く制御し、接合抵抗を再現性のある方法で調整できます。AlOxをNbベースの接合に組み込む試みは、Nbへの酸素}拡散 によって制限され、界面に欠陥のあるNbOxが形成され、損失が増大します。

酸化タンタル（TaOx）は、その化学的安定性とタンタルおよびニオブ電極との適合性から、代替バリア材料として注目を集めている。TaOxは真空を破ることなくin situで成長させることができ、一般的にNbOxよりも欠陥密度が低いため、TLS損失の低減に貢献する。^{[26] [22]構造的には、TaOxは}五酸化タンタル（Ta₂O₅）由来の非晶質またはナノ結晶相で構成され、歪んだTaO₆およびTaO₇多面体から構成される複数の結晶多形を示す。実際のデバイスでは、TaOxバリアは通常、局所的に変化する配位環境を持つ非晶質であり、比較的高い抵抗率のために達成可能な電流密度が制限される。

角を共有する NbO₆ 八面体を示す二酸化ニオブ (NbO₂) の結晶構造。

酸化ニオブ（NbOx）は、その複雑な非化学量論的化学構造と構造的不均一性のため、ジョセフソン接合におけるトンネル障壁としての性能が一般的に低い。Nb上の自然酸化物は、それぞれ金属相、半導体相、絶縁相に対応するNbO、NbO₂、Nb₂O₅の混合物である。この共存は、フィラメント状の伝導経路、ピンホール、接合再現性の低下など、不均一な障壁特性につながる。AlOxとは異なり、NbOxは自己制限的な成長を示さず、厚さは環境条件や表面条件に強く依存する。そのため、酸化されたNb表面は、不可避的なNbO界面層を有する不均一な酸化物スタックを形成し、超伝導量子ビットデバイスにおける損失の増加とコヒーレンスの低下に寄与する。 ^{[27] [28]}

ジルコニウム (黒) と酸素 (赤) 原子を示す二酸化ジルコニウム (ZrO₂) の正方晶結晶構造。

酸化ジルコニウム（ZrOx）は、高い酸素親和性とAlOxに比べて優れた化学的安定性を有することから、有望なバリア材料として注目されています。室温でのZrO₂の熱力学的安定相は単斜晶系ですが、最近の研究では、室温でスパッタリング法で作製した薄膜では正方晶系ZrOx結晶が安定化できることが実証されています。これらの特性により、ZrOxは構造均一性を向上させた人工トンネルバリアの魅力的な候補となっています。^[29]

金属障壁は、超伝導体-常伝導金属-超伝導体（SNS）ジョセフソン接合に用いられます。この接合では、薄い常伝導金属層が超伝導体間の弱結合を形成します。このような接合では、超伝導相関は近接効果によって媒介され、アンドレーエフ反射が輸送において中心的な役割を果たします。アルミニウムなどの金属は、NbベースのSNS接合の障壁として研究されてきましたが、界面安定性と厚さ制御が大きな課題となり、低損失量子ビット用途への適用が制限されています。^[22]

ジョセフソン方程式

単一のジョセフソン接合の図。AとBは超伝導体を表し、Cはそれらの間の弱い結合を表します。

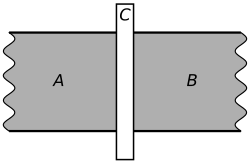
ジョセフソン効果は量子力学の法則を用いて計算できる。右に単一のジョセフソン接合の図を示す。超伝導体Aがギンツブルグ・ランダウ秩序パラメータ を 持ち、超伝導体Bがを持つと仮定する。これらは、2つの超伝導体におけるクーパー対の波動関数として解釈できる。接合の電位差が であれば、2つの超伝導体間のエネルギー差は となる。これは、各クーパー対が1電子の2倍の電荷を持つためである。したがって、この2状態量子系のシュレーディンガー方程式は以下の通りである。 ^[30]${\displaystyle \psi _{A}={\sqrt {n_{A}}}e^{i\phi _{A}}}$ ${\displaystyle \psi_{B}={\sqrt{n_{B}}}e^{i\phi_{B}}}$ ${\displaystyle V}$ ${\displaystyle 2eV}$

$${\displaystyle i\hbar {\frac {\partial }{\partial t}}{\begin{pmatrix}{\sqrt {n_{A}}}e^{i\phi _{A}}\\{\sqrt {n_{B}}}e^{i\phi _{B}}\end{pmatrix}}={\begin{pmatrix}eV&K\\K&-eV\end{pmatrix}}{\begin{pmatrix}{\sqrt {n_{A}}}e^{i\phi _{A}}\\{\sqrt {n_{B}}}e^{i\phi _{B}}\end{pmatrix}},}$$

ここで、定数は接合の特性です。上記の式を解くには、まず超伝導体Aの秩序パラメータの時間微分を計算します。 ${\displaystyle K}$

$${\displaystyle {\frac {\partial }{\partial t}}({\sqrt {n_{A}}}e^{i\phi _{A}})={\dot {\sqrt {n_{A}}}}e^{i\phi _{A}}+{\sqrt {n_{A}}}(i{\dot {\phi }}_{A}e^{i\phi _{A}})=({\dot {\sqrt {n_{A}}}}+i{\sqrt {n_{A}}}{\dot {\phi }}_{A})e^{i\phi _{A}},}$$

したがってシュレーディンガー方程式は次のようになります。

$${\displaystyle ({\dot {\sqrt {n_{A}}}}+i{\sqrt {n_{A}}}{\dot {\phi }}_{A})e^{i\phi _{A}}={\frac {1}{i\hbar }}(eV{\sqrt {n_{A}}}e^{i\phi _{A}}+K{\sqrt {n_{B}}}e^{i\phi _{B}}).}$$

接合を挟んだギンツブルグ・ランダウ秩序パラメータの位相差はジョセフソン位相と呼ばれる。

$${\displaystyle \varphi =\phi _{B}-\phi _{A}.}$$ したがって、シュレーディンガー方程式は次のように書き直すことができます。

$${\displaystyle {\dot {\sqrt {n_{A}}}}+i{\sqrt {n_{A}}}{\dot {\phi }}_{A}={\frac {1}{i\hbar }}(eV{\sqrt {n_{A}}}+K{\sqrt {n_{B}}}e^{i\varphi }),}$$

その複素共役方程式は次のようになります。

$${\displaystyle {\dot {\sqrt {n_{A}}}}-i{\sqrt {n_{A}}}{\dot {\phi }}_{A}={\frac {1}{-i\hbar }}(eV{\sqrt {n_{A}}}+K{\sqrt {n_{B}}}e^{-i\varphi }).}$$

2つの共役方程式を足し合わせて、次を消去します。 ${\displaystyle {\dot {\phi }}_{A}}$

$${\displaystyle 2{\dot {\sqrt {n_{A}}}}={\frac {1}{i\hbar }}(K{\sqrt {n_{B}}}e^{i\varphi }-K{\sqrt {n_{B}}}e^{-i\varphi })={\frac {K{\sqrt {n_{B}}}}{\hbar }}\cdot 2\sin \varphi .}$$

なので、次の式が成り立ちます。 ${\displaystyle {\dot {\sqrt {n_{A}}}}={\frac {{\dot {n}}_{A}}{2{\sqrt {n_{A}}}}}}$

$${\displaystyle {\dot {n}}_{A}={\frac {2K{\sqrt {n_{A}n_{B}}}}{\hbar }}\sin \varphi .}$$

ここで、2つの共役方程式を引き算して、次の式を消去します。 ${\displaystyle {\dot {\sqrt {n_{A}}}}}$

$${\displaystyle 2i{\sqrt {n_{A}}}{\dot {\phi }}_{A}={\frac {1}{i\hbar }}(2eV{\sqrt {n_{A}}}+K{\sqrt {n_{B}}}e^{i\varphi }+K{\sqrt {n_{B}}}e^{-i\varphi }),}$$

これにより、次のようになります。

$${\displaystyle {\dot {\phi }}_{A}=-{\frac {1}{\hbar }}(eV+K{\sqrt {\frac {n_{B}}{n_{A}}}}\cos \varphi ).}$$

同様に、超伝導体Bについては次のことが言えます。

$${\displaystyle {\dot {n}}_{B}=-{\frac {2K{\sqrt {n_{A}n_{B}}}}{\hbar }}\sin \varphi ,\,{\dot {\phi }}_{B}={\frac {1}{\hbar }}(eV-K{\sqrt {\frac {n_{A}}{n_{B}}}}\cos \varphi ).}$$

ジョセフソン位相の発展はであり、電荷キャリア密度の時間微分は電流に比例することに注意すると、上記の解はジョセフソン方程式を与える：^[31]${\displaystyle {\dot {\varphi }}={\dot {\phi }}_{B}-{\dot {\phi }}_{A}}$ ${\displaystyle {\dot {n}}_{A}}$ ${\displaystyle I}$ ${\displaystyle n_{A}\approx n_{B}}$

${\displaystyle I(t)=I_{c}\sin(\varphi (t))}$ （1）

${\displaystyle {\frac {\partial \varphi }{\partial t}}={\frac {2eV(t)}{\hbar }}}$ （2）

ここで、 とはジョセフソン接合の両端の電圧と電流であり、 は臨界電流と呼ばれる接合パラメータである。式(1)は第一ジョセフソン関係式または弱結合電流位相関係式と呼ばれ、式(2)は第二ジョセフソン関係式または超伝導相発展方程式式と呼ばれる。ジョセフソン接合の臨界電流は超伝導体の特性に依存し、温度や外部磁場などの環境要因の影響を受けることもある。 ${\displaystyle V(t)}$ ${\displaystyle I(t)}$ ${\displaystyle I_{c}}$

ジョセフソン定数は次のように定義されます。

$${\displaystyle K_{J}={\frac {2e}{h}}\,,}$$

そしてその逆は磁束量子である。

$${\displaystyle \Phi _{0}={\frac {h}{2e}}=2\pi {\frac {\hbar }{2e}}\,.}$$

超伝導相発展方程式は次のように表現できます。

$${\displaystyle {\frac {\partial \varphi }{\partial t}}=2\pi [K_{J}V(t)]={\frac {2\pi }{\Phi _{0}}}V(t)\,.}$$

次のように定義します。

$${\displaystyle \Phi =\Phi _{0}{\frac {\varphi }{2\pi }}\,,}$$

接合部の電圧は次のようになります。

$${\displaystyle V={\frac {\Phi _{0}}{2\pi }}{\frac {\partial \varphi }{\partial t}}={\frac {d\Phi }{dt}}\,,}$$

これはファラデーの電磁誘導の法則と非常によく似ています。しかし、この電圧は磁気エネルギーから生じるのではなく、超伝導体には磁場が存在しないため、キャリア（クーパー対）の運動エネルギーから生じることに注意してください。この現象は運動インダクタンスとも呼ばれます。

3つの主な効果

超伝導トンネル接合（一般的なジョセフソン接合の一種）の典型的な電流-電圧特性。縦軸の目盛りは50μA、横軸の目盛りは1mVである。におけるバーはDCジョセフソン効果を表し、の大きな値における電流は超伝導バンドギャップの有限値によるものであり、上記の式では再現されない。${\displaystyle V=0}$ ${\displaystyle \left|V\right|}$

ジョセフソン方程式から直接導かれる、ジョセフソンによって予測された主な効果は 3 つあります。

DCジョセフソン効果

DCジョセフソン効果とは、外部電磁場が存在しない状態で、トンネル効果によって絶縁体を横切る直流電流のことです。このDCジョセフソン電流は、ジョセフソン位相（絶縁体両端の位相差で、時間経過に関わらず一定）の正弦に比例し、 から までの値をとります。 ${\displaystyle -I_{c}}$ ${\displaystyle I_{c}}$

ACジョセフソン効果

接合にかかる電圧が一定であれば、位相は時間とともに直線的に変化し、電流は振幅と周波数を持つ正弦波交流（AC ）となります。これは、ジョセフソン接合が完璧な電圧-周波数変換器として機能することを意味します。 ${\displaystyle V_{DC}}$ ${\displaystyle I_{c}}$ ${\displaystyle K_{J}V_{DC}}$

逆ACジョセフソン効果

単一（角）周波数 のマイクロ波放射はジョセフソン接合に量子化されたDC電圧^[32]を誘導することができ、その場合ジョセフソン位相はの形を取り、接合の両端の電圧と電流は次のようになる。 ${\displaystyle \omega }$ ${\displaystyle \varphi (t)=\varphi _{0}+n\omega t+a\sin(\omega t)}$ $${\displaystyle V(t)={\frac {\hbar }{2e}}\omega (n+a\cos(\omega t)),{\text{ and }}I(t)=I_{c}\sum _{m=-\infty }^{\infty }J_{m}(a)\sin(\varphi _{0}+(n+m)\omega t),}$$

DC コンポーネントは次のとおりです。 $${\displaystyle V_{\text{DC}}=n{\frac {\hbar }{2e}}\omega ,{\text{ and }}I_{\text{DC}}=I_{c}J_{-n}(a)\sin \varphi _{0}.}$$

これはジョセフソン接合が完璧な周波数-電圧変換器のように動作することを意味し、^[33]これがジョセフソン電圧標準の理論的根拠となっている。

ジョセフソンインダクタンス

電流とジョセフソン位相が時間とともに変化すると、接合部における電圧降下もそれに応じて変化します。以下の導出に示すように、ジョセフソン関係式から、この挙動はジョセフソンインダクタンスと呼ばれる運動学的インダクタンスによってモデル化できることが分かります。^[34]

ジョセフソン関係式を次のように書き直す。

${\displaystyle {\begin{aligned}{\frac {\partial I}{\partial \varphi }}&=I_{c}\cos \varphi ,\\{\frac {\partial \varphi }{\partial t}}&={\frac {2\pi }{\Phi _{0}}}V.\end{aligned}}}$

ここで、連鎖律を適用して電流の時間微分を計算します。

${\displaystyle {\frac {\partial I}{\partial t}}={\frac {\partial I}{\partial \varphi }}{\frac {\partial \varphi }{\partial t}}=I_{c}\cos \varphi \cdot {\frac {2\pi }{\Phi _{0}}}V,}$

上記の結果をインダクタの 電流-電圧特性の形で整理すると、

${\displaystyle V={\frac {\Phi _{0}}{2\pi I_{c}\cos \varphi }}{\frac {\partial I}{\partial t}}=L(\varphi ){\frac {\partial I}{\partial t}}.}$

これはジョセフソン位相の関数としての運動インダクタンスの式を与える。

${\displaystyle L(\varphi )={\frac {\Phi _{0}}{2\pi I_{c}\cos \varphi }}={\frac {L_{J}}{\cos \varphi }}.}$

ここで、ジョセフソン接合の特性パラメータはジョセフソンインダクタンスと呼ばれます。 ${\displaystyle L_{J}=L(0)={\frac {\Phi _{0}}{2\pi I_{c}}}}$

ジョセフソン接合の運動学的挙動はインダクタのそれに類似していますが、関連する磁場は存在しないことに注意してください。この挙動は、磁場のエネルギーではなく、電荷キャリアの運動エネルギーに由来します。

ジョセフソンエネルギー

ジョセフソン接合と非線形インダクタの類似性に基づいて、超電流がジョセフソン接合を流れたときにそこに蓄えられるエネルギーを計算することができる。^[35]

接合を流れる超電流は、電流位相関係（CPR）によってジョセフソン位相と関連しています。

${\displaystyle I=I_{c}\sin \varphi .}$

超伝導相発展方程式はファラデーの法則に類似している。

${\displaystyle V=\operatorname {d} \!\Phi /\operatorname {d} \!t\,.}$

時刻 において、ジョセフソン位相が であると仮定する。その後の時刻 において、ジョセフソン位相は に変化した。接合におけるエネルギーの増加は、接合で行われた仕事に等しい。 ${\displaystyle t_{1}}$ ${\displaystyle \varphi _{1}}$ ${\displaystyle t_{2}}$ ${\displaystyle \varphi _{2}}$

${\displaystyle \Delta E=\int _{1}^{2}IV\operatorname {d} \!{t}=\int _{1}^{2}I\operatorname {d} \!\Phi =\int _{\varphi _{1}}^{\varphi _{2}}I_{c}\sin \varphi \operatorname {d} \!\left(\Phi _{0}{\frac {\varphi }{2\pi }}\right)=-{\frac {\Phi _{0}I_{c}}{2\pi }}\cos \Delta \varphi \,.}$

これは、ジョセフソン接合におけるエネルギー変化は、接合の初期状態と最終状態のみに依存し、経路には依存しないことを示しています。したがって、ジョセフソン接合に蓄えられるエネルギーは状態関数であり、以下のように定義されます。

${\displaystyle E(\varphi )=-{\frac {\Phi _{0}I_{c}}{2\pi }}\cos \varphi =-E_{J}\cos \varphi \,.}$

これはジョセフソン接合の特性パラメータであり、ジョセフソンエネルギーと呼ばれます。これはジョセフソンインダクタンスと の関係にあります。これと同等の別の定義もよく用いられます。 ${\displaystyle E_{J}=|E(0)|={\frac {\Phi _{0}I_{c}}{2\pi }}}$ ${\displaystyle E_{J}=L_{J}I_{c}^{2}}$ ${\displaystyle E(\varphi )=E_{J}(1-\cos \varphi )}$

もう一度、非線形磁気コイルインダクタは、電流が通過すると磁場に位置エネルギーを蓄積することに注意してください。ただし、ジョセフソン接合の場合は、超電流によって磁場は生成されません。代わりに、蓄積されるエネルギーは電荷キャリアの運動エネルギーから得られます。

RCSJモデル

抵抗容量シャント接合（RCSJ）モデル^{[36] [37]}または単にシャント接合モデルは、上記の2つの基本的なジョセフソン関係に加えて、実際のジョセフソン接合のACインピーダンスの影響を考慮しています。

テブナンの定理^[38]によれば、接合の交流インピーダンスは、理想的なジョセフソン接合に並列に接続されたコンデンサとシャント抵抗器^[39]で表すことができます。電流駆動の完全な式は次のようになります。 ${\displaystyle I_{\text{ext}}}$

${\displaystyle I_{\text{ext}}=C_{J}{\frac {\operatorname {d} \!V}{\operatorname {d} \!t}}+I_{c}\sin \varphi +{\frac {V}{R}},}$

ここで、最初の項は変位電流と実効容量、3 番目の項は法線電流と実効接合抵抗です。 ${\displaystyle C_{J}}$ ${\displaystyle R}$

ジョセフソン侵入深度

ジョセフソン侵入長は、外部から印加された磁場が長いジョセフソン接合に侵入する典型的な長さを表します。これは通常 と表記され、次式（SI単位）で与えられます。 ${\displaystyle \lambda _{J}}$

${\displaystyle \lambda _{J}={\sqrt {\frac {\Phi _{0}}{2\pi \mu _{0}d'j_{c}}}},}$

ここで、は磁束量子、は臨界超伝導電流密度（A/m ²）、超伝導電極のインダクタンスを特徴付ける^[40]${\displaystyle \Phi _{0}}$ ${\displaystyle j_{c}}$ ${\displaystyle d'}$

${\displaystyle d'=d_{I}+\lambda _{1}\tanh \left({\frac {d_{1}}{2\lambda _{1}}}\right)+\lambda _{2}\tanh \left({\frac {d_{2}}{2\lambda _{2}}}\right),}$

ここで、 はジョセフソン障壁（通常は絶縁体）の厚さ、は超伝導電極の厚さ、はそれらのロンドン侵入深さである。ジョセフソン侵入深さは、臨界電流密度が非常に低い場合、通常数μmから数mmの範囲となる。^[41]${\displaystyle d_{I}}$ ${\displaystyle d_{1}}$ ${\displaystyle d_{2}}$ ${\displaystyle \lambda _{1}}$ ${\displaystyle \lambda _{2}}$

参照

• パイジョセフソン接合
• φ ジョセフソン接合
• ジョセフソンダイオード
• アンドレーエフの反省
• 分数渦
• ギンツブルグ・ランダウ理論
• マクロな量子現象
• マクロな量子自己束縛
• 量子コンピュータ
• 量子ジャイロスコープ
• 高速単一磁束量子（RSFQ）
• セミフルクソン
• ゼロ点エネルギー
• ジョセフソン渦

参考文献

1. Josephson, BD (1962). 「超伝導トンネル効果における新たな効果の可能性」. Physics Letters . 1 (7): 251– 253. Bibcode :1962PhL.....1..251J. doi :10.1016/0031-9163(62)91369-0.
2. Josephson, BD (1974). 「トンネル超伝導電流の発見」. Reviews of Modern Physics . 46 (2): 251– 254. Bibcode :1974RvMP...46..251J. doi :10.1103/RevModPhys.46.251. S2CID  54748764.

   また、Josephson, BD (1974). "The Discovery of Tunneling Supercurrents". Europhysics News . 5 (3): 1– 5. Bibcode :1974ENews...5c...1J. doi :10.1051/epn/19740503001.

3. スティーブン・ストロガッツ、「Sync：自発的秩序の新たな科学」、ハイペリオン、2003年。
4. モンド研究所、イングランドの国家遺産リスト、ヒストリック・イングランド（2022年9月17日アクセス）
5. ジョセフソン、ブライアン・D.（1973年12月12日）「トンネル超伝導電流の発見（ノーベル賞受賞記念講演）」
6. Cohen, MH; Falicov, LM; Phillips, JC (1962年4月15日). 「超伝導トンネル効果」 . Physical Review Letters . 8 (8): 316– 318. Bibcode :1962PhRvL...8..316C. doi :10.1103/PhysRevLett.8.316.
7. デイッチ、ヴィッキー、ホッデソン、リリアン (2002). 『真の天才：ジョン・バーディーンの生涯と科学』ジョセフ・ヘンリー・プレス. p. 117. ISBN 9780309084086。
8. Anderson, PW; Rowell, JM (1963年3月15日). 「ジョセフソントンネル効果の可能性のある観測」 . Physical Review Letters . 10 (6): 230. Bibcode :1963PhRvL..10..230A. doi :10.1103/PhysRevLett.10.230.
9. US3335363A、アンダーソン、フィリップ W. & デイエム、アリ H.、「電極間の最小寸法を有する可変寸法の超伝導装置」、1967年8月8日発行 
10. 「1973年のノーベル物理学賞」ノーベル賞. 2023年3月1日閲覧。
11. 「2025年ノーベル物理学賞」NobelPrize.org . 2025年10月16日閲覧。
12. Schirber, Michael (2025-10-07). 「ノーベル賞：大規模量子トンネル効果」.物理学. 18 : 170. doi :10.1103/PhysRevLett.53.1260.
13. Anderson, PW; Dayem, AH (1964). 「超伝導薄膜ブリッジにおける無線周波数効果」. Physical Review Letters . 13 (6): 195. Bibcode :1964PhRvL..13..195A. doi :10.1103/PhysRevLett.13.195.
14. Dawe, Richard (1998年10月28日). 「SQUID：技術レポート – パート3：SQUID」. rich.phekda.org . 2011年7月27日時点のオリジナル（ウェブサイト）からのアーカイブ。 2011年4月21日閲覧。
15. Sato, Y.; Packard, R. (2012年10月) 「超流体ヘリウム干渉計」 Physics Today、31ページ。
16. Fulton, TA; Gammel, PL; Bishop, DJ; Dunkleberger, LN; Dolan, GJ (1989). 「小型トンネル接合回路におけるジョセフソン効果と充電効果の複合観測」. Physical Review Letters . 63 (12): 1307– 1310. Bibcode :1989PhRvL..63.1307F. doi :10.1103/PhysRevLett.63.1307. PMID  10040529.
17. Bouchiat、V.;ヴィオン、D.ジョイズ、P.エステベ、Ｄ．ミネソタ州デボレ (1998)。 「単一のクーパーペアによる量子コヒーレンス」。フィジカスクリプタ。T76 : 165。Bibcode :1998PhST...76..165B。土井：10.1238/Physica.Topical.076a00165。S2CID  250887469。
18. M. Tinkham,超伝導入門、第2版（McGraw-Hill、1996年）。
19. キルヒャー, CJ; 村上, M. (1980). 「ジョセフソン・トンネル接合電極材料」. Science 208 (4446): 944–949.
20. Raider, SI (1985). 「耐火電極を用いたジョセフソントンネル接合」IEEE Transactions on Magnetics 21 (2): 110–115.
21. シュワルツ、N.;フェイト、ED (1977)。 「アルファ (bcc) タンタルまたはベータ タンタル膜の核形成における不純物の影響」。電気化学協会ジャーナル 124 : 124–131。
22. Lacquaniti, V.; Gozzini, S.; Maggi, S.; Monticone, E.; Steni, R.; Andreone, D. (1999). 「AlおよびTaOxバリアを備えたNb系SNS接合によるプログラマブル・ジョセフソン電圧標準」IEEE Transactions on Applied Superconductivity 9 (2): 4245–4248.
23. Wright, J.; Chang, C.; Waters, D.; Lüpke, F.; Feenstra, R.; Raymond, L.; Koscica, R.; Khalsa, G.; Muller, D.; Xing, HG; Jena, D. (2021). 「未踏のMBE成長モードが超伝​​導NbNの新たな特性を明らかにする」. Physical Review Materials 5 : 024802. doi:10.1103/PhysRevMaterials.5.024802.
24. ラチョウスキー、A.ウォルニー、P.ディブコ、K。クリパラ、M. Nowakowski-Szklarek、K.ハイデル、M.ザク、M.フェドゥニェヴィチ、A.サウィッカ、M.クロミンスキー、W.グルザンカ、E. Skierbieszewski、C. (2025)。 「プラズマ支援分子線エピタキシーによって成長させたNbNベースのジョセフソン接合」。コミュニケーション資料 6 : 169. doi:10.1038/s43246-025-00891-3。
25. Liu, X.; Pan, K.; Zhang, Z.; Feng, Z. (2023). 「量子ビットにおけるAl/AlOx/Alジョセフソン接合の原子構造と化学組成の解明」. Applied Surface Science 640 : 158337. doi:10.1016/j.apsusc.2023.158337.
26. ポトルリ、R.;タンギララ、R.バウアーズ、Ｓ．バリオス、A.クマール、P.スシュコ、PV。パパス、DP;イーリー、S. (2025)。 「Ta₂O₅バリアを備えたタンタルジョセフソン接合の三層構造の作製と構造解析」。arXivプレプリント arXiv:2510.20114。
27. Celaschi, S.; Geballe, TH; Lowe, WP (1983). 「単結晶Nb/Nb₂O₅/Pbジョセフソン接合のトンネル特性」.応用物理学論文集 43 (8): 794–796. doi:10.1063/1.94595.
28. Hossain, N. NbOx薄膜の合成と特性評価。サスカチュワン大学、サスカトゥーン、カナダ、修士論文。
29. チョイ、J.オルシェフスキー、M.張、Ｌ．バライソフ、Z.バナジー、T.アガルワル、K.チョーダリー、S.アリアス、TA;ミュラー、DA;ファテミ、V。フックス、GD (2025)。 「低障壁ZrOxベースのジョセフソン接合」。APL マテリアル 13 : 111103.doi:10.1063/5.0296881。
30. 「ファインマン物理学講義 第3巻 第21章 古典的な文脈におけるシュレーディンガー方程式：超伝導セミナー、第21-9節 ジョセフソン接合」feynmanlectures.caltech.edu . 2020年1月3日閲覧。
31. バローネ, A.; パテルノ, G. (1982).ジョセフソン効果の物理学と応用. ニューヨーク:ジョン・ワイリー・アンド・サンズ. ISBN 978-0-471-01469-0。
32. Langenberg, DN; Scalapino, DJ; Taylor, BN; Eck, RE (1966-04-01). 「ジョセフソン接合におけるマイクロ波誘起DC電圧」. Physics Letters . 20 (6): 563– 565. Bibcode :1966PhL....20..563L. doi :10.1016/0031-9163(66)91114-0. ISSN  0031-9163.
33. Levinsen, MT; Chiao, RY; Feldman, MJ; Tucker, BA (1977-12-01). 「逆交流ジョセフソン効果電圧標準」. Applied Physics Letters . 31 (11): 776– 778. Bibcode :1977ApPhL..31..776L. doi :10.1063/1.89520. ISSN  0003-6951.
34. Devoret, M.; Wallraff, A.; Martinis, J. (2004). 「超伝導量子ビット：短いレビュー」. arXiv : cond-mat/0411174 .
35. マイケル・ティンカム、「超伝導入門」、クーリエコーポレーション、1986年。
36. McCumber, DE (1968-06-01). 「超伝導弱結合接合の直流電圧-電流特性に対する交流インピーダンスの影響」. Journal of Applied Physics . 39 (7): 3113– 3118. Bibcode :1968JAP....39.3113M. doi :10.1063/1.1656743. ISSN  0021-8979.
37. Chakravarty, Sudip; Ingold, Gert-Ludwig; Kivelson, Steven; Zimanyi, Gergely (1988-03-01). 「抵抗シャントジョセフソン接合アレイの量子統計力学」. Physical Review B. 37 ( 7): 3283– 3294. Bibcode :1988PhRvB..37.3283C. doi :10.1103/PhysRevB.37.3283. PMID:  9944915.
38. 「ACテブナンの定理」. hyperphysics.phy-astr.gsu.edu . 2020年1月3日閲覧。
39. 「RF SQUIDのダイナミクス」phelafel.technion.ac.il . 2021年6月13日時点のオリジナルよりアーカイブ。2020年1月11日閲覧。
40. Weihnacht, M. (1969). 「DCジョセフソン電流に対する膜厚の影響」. Physica Status Solidi B. 32 ( 2): 169. Bibcode :1969PSSBR..32..169W. doi :10.1002/pssb.19690320259.
41. ヴェルナー、バッケル;クライナー、ラインホルト (2004)。Supraleitung (6 版)。テュービンゲン: Wiley-VCH Verlag GmbH&Co.KGaA。 p. 67.ISBN​ 3527403485。