ケルビン・フォークト物質
粘弾性材料のモデル

ケルビン・フォークト材料（フォークト材料とも呼ばれる）は、典型的なゴムのような性質を示す最も単純な粘弾性材料モデルである。長時間スケール（緩やかな変形）では純粋に弾性を示すが、急速な変形に対しては抵抗を示す。このモデルは、1865年にイギリスの物理学者ケルビン卿[1]と、 1890年にドイツの物理学者ヴォルデマール・フォークト[2]によってそれぞれ独立して開発された[3]。

意味

ケルビン-フォークトモデルの概略図。

ケルビン-フォークト モデル (フォークト モデルとも呼ばれます) は、図に示すように、 純粋に粘性のダンパーと純粋に弾性のスプリングが並列に接続されて表されます。

代わりに、これら 2 つの要素を直列に接続すると、マクスウェル材料のモデルが得られます。

モデルの 2 つのコンポーネントは並列に配置されているため、各コンポーネントのひずみは同じです。

ε 合計 ＝ ε S ＝ ε D 。 {\displaystyle \varepsilon_{\text{合計}}=\varepsilon_{\rm{S}}=\varepsilon_{\rm{D}}.}

ここで、下付き文字Dはダンパーの応力-ひずみを示し、下付き文字Sはバネの応力-ひずみを示す。同様に、総応力は各部品の応力の合計となる。[4]

σ 合計 ＝ σ S + σ D 。 {\displaystyle \sigma _{\text{合計}}=\sigma _{\rm {S}}+\sigma _{\rm {D}}.}

これらの式から、ケルビン・フォークト材料では、応力 σ、ひずみ ε 、および時間tに対するそれらの変化率は、次の形式の式で表されます。

σ （ t ） ＝ E ε （ t ） + η d ε （ t ） d t 、 {\displaystyle \sigma (t)=E\varepsilon (t)+\eta {\frac {d\varepsilon (t)}{dt}},}

またはドット表記では：

σ ＝ E ε + η ε ˙ 、 {\displaystyle \sigma =E\varepsilon +\eta {\dot {\varepsilon }},}

ここで、Eは弾性係数、は粘度です。この式は、材料の せん断応力または法線応力のどちらにも適用できます。 η {\displaystyle \eta}

突然のストレスの影響

一定応力下における無次元変形の無次元時間依存性

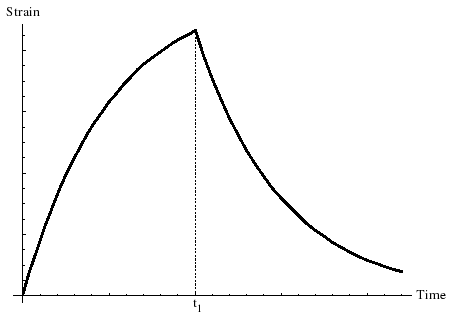
ケルビン・フォークト材料に一定の応力を突然加えると、変形は純粋な弾性材料の変形に近づき、その差は指数関数的に減少します。[4] σ 0 {\displaystyle \sigma _{0}} σ 0 / E {\displaystyle \sigma _{0}/E}

ε （ t ） ＝ σ 0 E （ 1 − e − t / τ R ） 、 {\displaystyle \varepsilon (t)={\frac {\sigma _{0}}{E}}(1-e^{-t/\tau _{R}}),}

ここでtは時間、は遅延時間です。 τ R ＝ η E {\displaystyle \tau _{R}={\frac {\eta }{E}}}

時刻 に材料を解放すると、弾性要素は変形がゼロになるまで材料の動きを遅らせます。この動きの遅れは次の式に従います。 t 1 {\displaystyle t_{1}}

ε （ t > t 1 ） ＝ ε （ t 1 ） e − （ t − t 1 ） / τ R 。 {\displaystyle \varepsilon (t>t_{1})=\varepsilon (t_{1})e^{-(t-t_{1})/\tau _{R}}.}

この図は、無次元変形の無次元時間依存性を示しています。図では、材料にかかる応力は時刻 に負荷され、その後の無次元時間 に解放されます。 E ε （ t ） σ 0 {\displaystyle {\frac {E\varepsilon (t)}{\sigma _{0}}}} t / τ R {\displaystyle t/\tau_{R}} t ＝ 0 {\displaystyle t=0} t 1 ∗ ＝ t 1 / τ R {\displaystyle t_{1}^{*}=t_{1}/\tau_{R}}

すべての変形は可逆的（ただし突然ではない）なので、ケルビン・フォークト物質は固体です。

Voigt モデルは、無限の時間制限で歪みが一定に近づくため、Maxwell モデルよりも現実的にクリープを予測します。

リム t → ∞ ε ＝ σ 0 E 、 {\displaystyle \lim _{t\to \infty }\varepsilon ={\frac {\sigma _{0}}{E}},}

一方、マクスウェルモデルはひずみと時間の間に線形関係があると予測しますが、多くの場合これは当てはまりません。ケルビン・フォークトモデルはクリープの予測には有効ですが、応力負荷が除去された後の緩和挙動を記述するのには適していません。

動的弾性率

ケルビン・フォークト材料の 複素動的弾性率は次のように表されます。

E ⋆ （ ω ） ＝ E 0 （ 1 + 私 ω τ ） 。 {\displaystyle E^{\star }(\omega )=E_{0}(1+i\omega \tau ).}

したがって、動的弾性係数の実数部と虚数部はそれぞれ貯蔵弾性係数と呼ばれます。 E ′ {\displaystyle E^{\prime}} E ′ ′ {\displaystyle E^{\プライム \プライム }}

E ′ ＝ ℜ [ E ⋆ （ ω ） ] 、 {\displaystyle E^{\prime }=\Re [E^{\star }(\omega )],}
E ′ ′ ＝ ℑ [ E ⋆ （ ω ） ] ＝ E 0 ω τ 。 {\displaystyle E^{\prime \prime }=\Im [E^{\star }(\omega )]=E_{0}\omega \tau .}

は定数であるのに対し、は周波数に正比例することに注意してください（ここで時間スケールは比例定数です）。この定数に角周波数を乗じたものは、損失弾性率と呼ばれることがよくあります。 E ′ {\displaystyle E^{\prime}} E ′ ′ {\displaystyle E^{\プライム \プライム }} τ {\displaystyle \tau} τ {\displaystyle \tau} ω {\displaystyle \omega } η ＝ ω τ {\displaystyle \eta =\omega \tau }

参考文献

  1. ^ 「IV. 金属の弾性と粘性について」.ロンドン王立協会紀要. 14 : 289–297 . 1865年12月31日. doi :10.1098/rspl.1865.0052. ISSN  0370-1662.
  2. ^ フォークト、ヴォルダーマール (1890)。 「Ueber die innere Reibung der festen Körper, insbesondere der Krystalle」。Abhandlungen der Königlichen Gesellschaft von Wissenschaften zu Göttingen (ドイツ語)。36：3-47。
  3. ^ Rajagopal, KR (2009). 「ケルビン・フォークトモデルの再評価と一般化に関する注記」 . Mechanics Research Communications . 36 (2): 232– 235. doi :10.1016/j.mechrescom.2008.09.005.
  4. ^ ab マイヤーズ、マーク・アンドレ、チャウラ、クリシャン・クマール (1999). 「セクション13.11」. 材料の機械的挙動. ケンブリッジ大学出版局. pp.  570– 580. ISBN 978-1-107-39418-6。

参照

「https://en.wikipedia.org/w/index.php?title=ケルビン–フォークト_material&oldid=1292049714」より取得