
数学のグラフ理論分野において、クライングラフは2つの異なるが関連のある正則グラフであり、それぞれ84辺を持つ。それぞれは種数3の有向曲面に埋め込むことができ、双対グラフを形成する。
3次クライングラフ
| 3正則クライングラフ | |
|---|---|
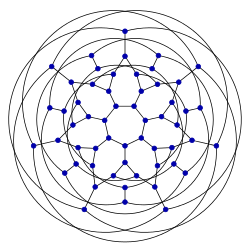 | |
| 名前の由来 | フェリックス・クライン |
| 頂点 | 56 |
| エッジ | 84 |
| 半径 | 6 |
| 直径 | 6 |
| 胴回り | 7 |
| 自己同型 | 336 |
| 彩色数 | 3 |
| 色指数 | 3 |
| 本の厚さ | 3 |
| キュー番号 | 2 |
| プロパティ | 対称 立方 ハミルトニアン |
| グラフとパラメータの表 | |
これは、フェリックス・クラインにちなんで名付けられた、 56 個の頂点と 84 個の辺を持つ3 次正則(立方) グラフです。
これはハミルトニアンであり、彩色数3、彩色指数3、半径6、直径6、内周7である。また、3頂点連結、3辺連結のグラフである。本の厚さは3、キュー数は2である。 [1]
これは種数-3の有向面(クラインの四次曲面として表すことができる)に埋め込むことができ、24個の七角形面を持つクラインの写像、シュレーフリ記号{7,3} 8を形成します。
フォスター調査によると、F056Bと呼ばれるクライングラフは、56頂点を持つ二部ではない唯一の立方対称グラフです。[2]
これは28頂点のコクセターグラフから導出できる。[3]
代数的性質
クライングラフの自己同型群は位数336の群PGL 2 (7)であり、その 正規部分群としてPSL 2 (7)を持つ。この群はその半辺に推移的に作用するため、クライングラフは対称グラフである。
この56頂点のクライングラフの特性多項式は次のようになる。
 |
 |
7正則クライングラフ
| 7正則クライングラフ | |
|---|---|
 | |
| 名前の由来 | フェリックス・クライン |
| 頂点 | 24 |
| エッジ | 84 |
| 半径 | 3 |
| 直径 | 3 |
| 胴回り | 3 |
| 自己同型 | 336 |
| 彩色数 | 4 |
| 色指数 | 7 |
| プロパティ | 対称 ハミルトニアン |
| グラフとパラメータの表 | |
これは、フェリックス・クラインにちなんで名付けられた、 24 個の頂点と 84 個の辺を持つ7正則グラフです。
これはハミルトニアンであり、彩色数4、彩色指数7、半径 3、直径 3、胴回り3 です。
これは種数3の有向曲面に埋め込むことができ、56個の三角形面を持つクライン写像の双対を形成し、シュレーフリ記号{3,7} 8となる。[4]
これは交差配列を持つ唯一の距離正則グラフであるが、距離推移グラフではない。[5]
代数的性質
7 価クライン グラフの自己同型群は、3 次クライン マップと同じ 336 次群であり、同様にその半辺に対して推移的に作用します。
この24頂点のクライングラフの特性多項式はに等しい。[6]

参考文献
- ^ Wolz, Jessica; SATを用いた線形レイアウトのエンジニアリング。修士論文、テュービンゲン大学、2018年
- ^ Conder, M. ; Dobcsányi, P. (2002). 「768頂点までの三価対称グラフ」. J. Combin. Math. Combin. Comput . 40 : 41–63 .。
- ^ Dejter、イタロ J. (2012)。 「コクセターグラフからクライングラフへ」。グラフ理論ジャーナル。70 (1): 1–9 . arXiv : 1002.1960。土井:10.1002/jgt.20597。MR 2916063。
- ^ Schulte, Egon; Wills, JM (1985). 「種数3のリーマン面上のフェリックス・クラインの写像{3, 7}8の多面体実現」. J. London Math. Soc . s2-32 (3): 539– 547. doi :10.1112/jlms/s2-32.3.539.
- ^ アンドリース、ブラウワー;コーエン、アルジェ。ノイマイヤー、アーノルド (1989)。距離-正規グラフ。スプリンガー・フェルラーグ。 p. 386.ISBN 978-0-387-50619-7。
- ^ van Dam, ER; Haemers, WH; Koolen, JH; Spence, E. (2006). 「スペクトルによるグラフの距離正則性の特徴づけ」J. Combin. Theory Ser. A . 113 (8): 1805– 1820. doi : 10.1016/j.jcta.2006.03.008 .


