区分線形継続

単体接続、あるいは区分線形接続（AllgowerとGeorg）^{[1] [2]}は、 1パラメータ接続法であり、小規模から中規模の埋め込み空間に適しています。このアルゴリズムは、（AllgowerとGnutzman） ^{[3]および（AllgowerとSchmidt） [4]}によって高次元多様体を計算するために一般化されました。

輪郭を描くアルゴリズムは単体継続アルゴリズムであり、視覚化しやすいため、アルゴリズムの良い入門書として役立ちます。

等高線図

等高線プロット問題は、（滑らかなスカラー値関数）のゼロ（等高線）を正方形内で見つけることである。 ${\displaystyle f(x,y)=0\,}$ ${\displaystyle f(\cdot )\,}$ ${\displaystyle 0\leq x\leq 1,0\leq y\leq 1\,}$

正方形は、通常、正方格子の頂点に点を導入し、各頂点におけるの値の表を作成し、各正方形を2つの三角形に分割することによって、小さな三角形に分割されます。三角形の頂点におけるの値は、各三角形上の への一意の区分線形補間を定義します。この補間を頂点を持つ三角形上に記述する一つの方法は、 次の方程式の集合です。 ${\displaystyle ih_{x}\leq x\leq (i+1)h_{x}\,}$ ${\displaystyle jh_{y}\leq y\leq (j+1)h_{y}\,}$ ${\displaystyle f(x_{i},y_{j})\,}$ ${\displaystyle (i,j)\,}$ ${\displaystyle f(x_{i},y_{j})\,}$ ${\displaystyle lf(x,y)\,}$ ${\displaystyle f(\cdot )\,}$ ${\displaystyle (x_{0},y_{0}),~(x_{1},y_{1}),~(x_{2},y_{2})\,}$

${\displaystyle (x,y)=(x_{0},y_{0})+(x_{1}-x_{0},y_{1}-y_{0})s+(x_{2}-x_{0},y_{2}-y_{0})t\,}$

${\displaystyle 0\leq s\,}$

${\displaystyle 0\leq t\,}$

${\displaystyle s+t\leq 1\,}$

${\displaystyle lf(x,y)=f(x_{0},y_{0})+(f(x_{1},y_{1})-f(x_{0},y_{0}))s+(f(x_{2},y_{2})-f(x_{0},y_{0}))t\,}$

最初の4つの方程式は について解くことができ（これにより元の三角形が直角単位三角形に写像されます）、残りの方程式は の補間値を与えます。三角形のメッシュ全体にわたって、この区分線形補間は連続です。 ${\displaystyle (s,t)\,}$ ${\displaystyle f(\cdot )\,}$

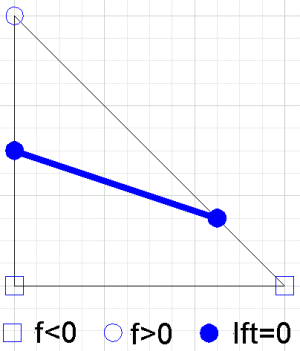
個々の三角形上の補間曲線は線分（2つの平面の交点上の区間）です。この線分の方程式は求まりますが、線分が三角形の辺と交差する点は線分の端点となります。

区分線形補間の輪郭は、これらの線分からなる曲線の集合である。とを結ぶ辺上の任意の点は、次のように表される。 ${\displaystyle (x_{0},y_{0})\,}$ ${\displaystyle (x_{1},y_{1})\,}$

${\displaystyle (x,y)=(x_{0},y_{0})+t(x_{1}-x_{0},y_{1}-y_{0}),\,}$

の範囲内にあり、エッジ上の線形補間は ${\displaystyle t\,}$ ${\displaystyle (0,1)\,}$

${\displaystyle f\sim f_{0}+t(f_{1}-f_{0})\,}$

設定${\displaystyle f=0\,}$

${\displaystyle t=-f_{0}/(f_{1}-f_{0})\,}$ そして${\displaystyle (x,y)=(x_{0},y_{0})-f_{0}*(x_{1}-x_{0},y_{1}-y_{0})/(f_{1}-f_{0})\,}$

これは辺の値のみに依存するため、この辺を共有するすべての三角形は同じ点を生成するため、輪郭線は連続的になります。各三角形は個別にテストすることができ、すべての三角形をチェックすれば、輪郭線曲線の集合全体を見つけることができます。

区分線形継続

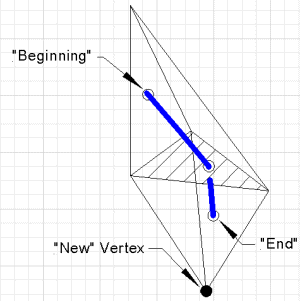
区分線形継続は、等高線図（Dobkin、Levy、Thurston、Wilks）^[5]に似ていますが、高次元です。このアルゴリズムは以下の結果に基づいています。

補題1

F(x)が にマッピングされる場合、単体の頂点における関数値と一致する '(n-1)' 次元単体上に一意の線形補間が存在します。${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n-1}}$

'(n-1)'次元単体はn個の頂点を持ち、関数Fは各頂点に'n'次元ベクトルを割り当てます。単体は凸であり、単体内の任意の点は頂点の凸結合です。つまり、

xがn個の頂点を持つ(n-1)次元単体の内部にある場合、次のような 正のスカラーが存在する。${\displaystyle v_{i}}$ ${\displaystyle 0<\alpha _{i}}$

${\displaystyle \mathbf {x} =\sum _{i}\alpha _{i}\mathbf {v} _{i}}$

${\displaystyle \sum _{i}\alpha _{i}=1.\,}$

単体の頂点が線型独立である場合、非負スカラーは各点xに対して一意であり、 xの重心座標と呼ばれます。これらのスカラーは、次の式によって 一意の補間値を決定します。${\displaystyle \alpha}$

${\displaystyle LF=\sum _{i}\alpha _{i}F(\mathbf {v} _{i})}$

補題2

(n-1)次元単体をテストして、原点が含まれているかどうかを判定できます。

基本的に2つのテストがあります。最初に使用されたテストは、単体の頂点に、その頂点の座標の符号(+/-)のベクトルでラベルを付けるものです。例えば、頂点(.5,-.2,1.)は(+,-,+)とラベル付けされます。ラベルが長さ0,1,2,3,4,...nの「+」記号の文字列で始まる頂点がある場合、単体は完全にラベル付けされていると呼ばれます。完全にラベル付けされた単体は、原点の近傍を含みます。これは意外に思われるかもしれませんが、この結果の根底にあるのは、完全にラベル付けされた単体の各座標に対して、「+」のベクトルと「-」のベクトルが存在するということです。言い換えれば、座標軸に平行な辺を持ち、単体を覆う最小の立方体は、0の反対側に2つの面（つまり、各座標に対して「+」と「-」）を持ちます。

2つ目のアプローチはベクトルラベリングと呼ばれます。これは単体の頂点の重心座標に基づいています。まず原点の重心座標を求め、次に単体が原点を含むかどうかを判定するには、すべての重心座標が正で、その合計が1未満であるかどうかを単純に確認します。

補題3

ピボット操作に対して不変である三角形分割（コクセター・フロイデンタール・キューン三角形分割[1]）が存在する。 ${\displaystyle P_{v_{i}}(v_{0},v_{1},...,v_{n}):=(v_{0},v_{1},...,v_{i-1},{\チルダ {v}}_{i},v_{i+1},...,v_{n})}$ どこ ${\displaystyle {\チルダ {v}}_{i}=\left\{{\begin{array}{lcl}v_{1}+v_{n}-v_{0}&&i=0\\v_{i+1}+v_{i-1}-v_{i}&\qquad \qquad &0\\v_{n-1}+v_{0}-v_{n}&&i=n\\\end{配列}}\right.}$

参考文献

1. Eugene L. Allgower、K. Georg、「数値継続法入門」、SIAM Classics in Applied Mathematics 45、2003年。
2. EL Allgower、K. Georg、「固定点と方程式の解を近似するための単純法と継続法」、SIAM Review、第22巻、28-85、1980年。
3. Eugene L. Allgower、Stefan Gnutzmann、「暗黙的に定義された2次元表面の区分線形近似アルゴリズム」、SIAM Journal on Numerical Analysis、第24巻、第2号、452-469、1987年。
4. Eugene L. Allgower、Phillip H. Schmidt、「暗黙的に定義された多様体の区分線形近似のアルゴリズム」、SIAM Journal on Numerical Analysis、第22巻、第2号、322-346、1985年4月。
5. David P. Dobkin、Silvio VF Levy、William P. Thurston、Allan R. Wilks、「区分線形近似による輪郭トレース」、ACM Transactions on Graphics、9(4) 389-423、1990年。