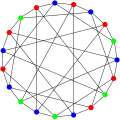
| ロバートソングラフ | |
|---|---|
 ロバートソングラフはハミルトングラフです。 | |
| 名前の由来 | ニール・ロバートソン |
| 頂点 | 19 |
| エッジ | 38 |
| 半径 | 3 |
| 直径 | 3 |
| 胴回り | 5 |
| 自己同型 | 24 ( D 12 ) |
| 彩色数 | 3 |
| 色指数 | 5 [1] |
| 本の厚さ | 3 |
| キュー番号 | 2 |
| プロパティ | ケージ ハミルトニアン |
| グラフとパラメータの表 | |
数学のグラフ理論の分野において、ロバートソングラフまたは(4,5)ケージは、ニール・ロバートソンにちなんで名付けられた19の頂点と38の辺を持つ4正則 無向グラフである。[2] [3]
ロバートソングラフは唯一の(4,5)-ケージグラフであり、1964年にロバートソンによって発見されました。[4]ケージグラフとしては、内周が5の最小の4-正則グラフです。
彩度数3、彩度指数5、直径3、半径3で、4頂点連結かつ4辺連結である。本の厚さは3、列数は2である。 [5]
ロバートソン グラフも、5,376 個の異なる有向ハミルトン サイクルを持つ ハミルトン グラフです。
ロバートソングラフは、警官番号4を持つ最も小さいグラフの1つです。[6]
代数的性質
ロバートソングラフは頂点推移グラフではない。その完全自己同型群は、回転と反射の両方を含む正十二角形の対称群である位数24の二面体群と同型である。 [7]
ロバートソングラフの 特性多項式は
ギャラリー
参考文献
- ^ Weisstein, Eric W.「クラス2グラフ」。MathWorld。
- ^ Weisstein, Eric W.「ロバートソングラフ」。MathWorld。
- ^ Bondy, JA、Murty、「USRグラフ理論とその応用」、ニューヨーク:ノースホランド、237ページ、1976年。
- ^ Robertson, N. 「内周5、価数4の最小グラフ」Bull. Amer. Math. Soc. 70, 824-825, 1964.
- ^ ジェシカ・ウォルツ、「 SATを用いた線形レイアウトのエンジニアリング」。修士論文、テュービンゲン大学、2018年
- ^ Turcotte, J., & Yvon, S. (2021). 4-cop-winグラフは少なくとも19個の頂点を持つ.離散応用数学,301,74-98.
- ^ Geoffrey Exoo & Robert Jajcay、「Dynamic cage survey」、Electr. J. Combin. 15、2008年。