半暗黙的オイラー法

数学において、半暗黙的オイラー法（シンプレクティックオイラー法、半明示的オイラー法、オイラー・クローマー法、ニュートン・シュテルマー・ベルレ法（NSV）とも呼ばれる）は、古典力学に現れる常微分方程式系であるハミルトン方程式を解くためのオイラー法の改良法である。これはシンプレクティック積分法であるため、標準的なオイラー法よりも優れた結果をもたらす。

起源

この方法はニュートンの『プリンキピア』 ^[1]にまで遡り、何度も発見されては忘れ去られてきました。リチャード・ファインマンがファインマン講義（第1巻、第9.6節）で回想しているとおりです。^[2]現代では、この方法は1956年にルネ・ド・フォージェラエールによってプレプリントで再発見されましたが、正式には出版されなかったものの、その後の高次シンプレクティック法の研究に影響を与えました。^[3]

設定

半暗黙的オイラー法は、次の形式の微分方程式のペアに適用できる^[要出典]

${\displaystyle {\begin{aligned}{dx \over dt}&=f(t,v)\\{dv \over dt}&=g(t,x),\end{aligned}}}$

ここで、 fとgは与えられた関数である。ここで、xとvはスカラーまたはベクトルである。ハミルトン力学における運動方程式は、ハミルトニアンが以下の形式である場合にこの形をとる。

${\displaystyle H=T(t,v)+V(t,x).\,}$

微分方程式は初期条件で解く。

${\displaystyle x(t_{0})=x_{0},\qquad v(t_{0})=v_{0}.}$

方法

半暗黙的オイラー法は、反復によって 近似離散解を生成する。

${\displaystyle {\begin{aligned}v_{n+1}&=v_{n}+g(t_{n},x_{n})\,\Delta t\\[0.3em]x_{n+1}&=x_{n}+f(t_{n},v_{n+1})\,\Delta t\end{aligned}}}$

ここで、Δ tは時間ステップであり、t _n = t ₀ + n Δ tはnステップ後の時間です。

標準オイラー法との違いは、半暗黙的オイラー法ではx _{n +1}の式にv _{n +1}を使用するのに対し、オイラー法ではv _{n を}使用することです。

負の時間ステップの方法を の計算に適用し、整理すると、半暗黙的オイラー法の2番目の変種が得られる。 ${\displaystyle (x_{n},v_{n})}$ ${\displaystyle (x_{n+1},v_{n+1})}$

${\displaystyle {\begin{aligned}x_{n+1}&=x_{n}+f(t_{n},v_{n})\,\Delta t\\[0.3ex]v_{n+1}&=v_{n}+g(t_{n},x_{n+1})\,\Delta t\end{aligned}}}$

同様の特性を持っています。

半暗黙的オイラー法は、標準オイラー法と同様に、一次積分器です。つまり、Δtオーダーの大域誤差を生じます。しかし、半暗黙的オイラー法は標準法とは異なり、シンプレクティック積分器です。その結果、半暗黙的オイラー法はエネルギーをほぼ保存します（ハミルトニアンが時間に依存しない場合）。多くの場合、標準オイラー法を適用するとエネルギーは着実に増加し、精度が大幅に低下します。

半暗黙的オイラー法の2つの変種を交互に用いると、ある単純化ではシュテルマー・ヴェルレ積分になり、また少し異なる単純化ではリープフロッグ積分になり、誤差の次数とエネルギー保存の次数の両方が増加します。^[1]

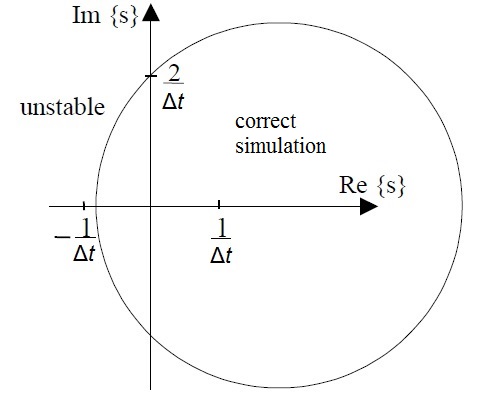
半暗黙法の安定領域はNiiranen ^[4]によって提唱されたが、彼の論文では半暗黙オイラー法は対称オイラー法と誤解を招くような名称で呼ばれていた。半暗黙法は、特性方程式の複素根が下図の円内にある場合、シミュレートされたシステムを正しくモデル化する。実根の場合、安定領域は基準となる円の外側に広がる。${\displaystyle s>-2/\Delta t}$

ご覧のとおり、半陰解法は、左半平面に根を持つ安定系と右半平面に根を持つ不安定系の両方を正しくシミュレートできます。これは、前進（標準）オイラー法や後退オイラー法に比べて明らかに有利です。前進オイラー法は、根の負の実部が虚軸に近づくと、実系よりも減衰が小さくなる傾向があります。一方、後退オイラー法は、根が右半平面にある場合でも、系が安定していることを示す可能性があります。

例

フックの法則を満たすバネの運動は次のように表される。

${\displaystyle {\begin{aligned}{\frac {dx}{dt}}&=v(t)\\[0.2em]{\frac {dv}{dt}}&=-{\frac {k}{m}}\,x=-\omega ^{2}\,x.\end{aligned}}}$

この方程式の半暗黙的オイラー法は

${\displaystyle {\begin{aligned}v_{n+1}&=v_{n}-\omega ^{2}\,x_{n}\,\Delta t\\[0.2em]x_{n+1}&=x_{n}+v_{n+1}\,\Delta t.\end{aligned}}}$

2番目の式に1番目の式で与えられた式 を代入すると、反復は次の行列形式で表すことができます。${\displaystyle v_{n+1}}$

${\displaystyle {\begin{bmatrix}x_{n+1}\\v_{n+1}\end{bmatrix}}={\begin{bmatrix}1-\omega ^{2}\Delta t^{2}&\Delta t\\-\omega ^{2}\Delta t&1\end{bmatrix}}{\begin{bmatrix}x_{n}\\v_{n}\end{bmatrix}},}$

行列の 行列式は 1なので、変換は面積を保存します。

反復計算は修正されたエネルギー汎関数を正確に保存し、（十分に小さいステップサイズの場合）正確な軌道から だけずれた安定な周期軌道をもたらします。正確な円周周波数は、数値近似において 倍に増加します。 ${\displaystyle E_{h}(x,v)={\tfrac {1}{2}}\left(v^{2}+\omega ^{2}\,x^{2}-\omega ^{2}\Delta t\,vx\right)}$ ${\displaystyle O(\Delta t)}$ ${\displaystyle \omega }$ ${\displaystyle 1+{\tfrac {1}{24}}\omega ^{2}\Delta t^{2}+O(\Delta t^{4})}$

参考文献

1. ハイラー、エルンスト;ルビッチ、クリスチャン。ワナー、ゲルハルト (2003)。 「Störmer/Verlet 法によって示される幾何学的数値積分」。アクタ ヌメリカ。12 : 399–450。書誌コード:2003AcNum..12..399H。CiteSeerX  10.1.1.7.7106。土井：10.1017/S0962492902000144。S2CID  122016794。
2. ファインマン、リチャード・P (1963). 『ファインマン物理学講義』第1巻、第9.6節。
3. Skeel, Robert D.; Cieśliński, Jan L. (2020). 「ルネ・ド・ヴォーゲラエレによる有名な未発表プレプリント『ハミルトン方程式の接触変換特性を保持する積分法』について」arXiv : 2003.12268 [math.NA].
4. Niiranen, Jouko: 電気機械シミュレーションのための高速かつ正確な対称オイラーアルゴリズム Proceedings of the Electrimacs'99、1999 年 9 月 14 ～ 16 日、ポルトガル、リスボン、第 1 巻、71 ～ 78 ページ。

• Nikolic, Branislav K. 「オイラー・クロマー法」.デラウェア大学. 2021年9月29日閲覧。
• Vesely, Franz J. (2001).計算物理学入門（第2版）. Springer. pp. 117. ISBN 978-0-306-46631-1。
• ジョルダーノ, ニコラス・J.; 中西久雄 (2005年7月).計算物理学(第2版). ベンジャミン・カミングス. ISBN 0-13-146990-8。