理論計算機科学の一分野であるオートマトン理論において、ω-オートマトン(またはストリームオートマトン)は、有限オートマトンの一種であり、有限の文字列ではなく無限の文字列を入力として動作します。ω-オートマトンには停止がないため、単純な受理状態の集合ではなく、多様な受理条件を持ちます。
ω-オートマトン(ω-オートマトン)は、ハードウェア、オペレーティングシステム、制御システムなど、終了することが想定されていないシステムの挙動を規定するのに役立ちます。このようなシステムでは、「すべてのリクエストに対して、最終的には確認応答が続く」といった性質、あるいはその否定形である「確認応答が続かないリクエストが存在する」といった性質を規定したい場合があります。前者は無限語の性質であり、有限のシーケンスがこの性質を満たすとは言えません。
ω-オートマトンには、ビュッヒ・オートマトン、ラビン・オートマトン、ストリート・オートマトン、パリティ・オートマトン、ミュラー・オートマトンなどがあり、それぞれ決定性または非決定性である。これらのω-オートマトンのクラスは、受理条件のみが異なる。決定性ビュッヒ・オートマトンを除き、これらはすべて正規ω-言語を正確に認識する。決定性ビュッヒ・オートマトンのみは他のすべてのオートマトンよりも厳密に弱い。これらのすべてのタイプのオートマトンは同じω-言語の集合を認識するが、与えられたω-言語に対する表現の簡潔さはそれぞれ異なる。
決定論的ωオートマトン
正式には、決定論的ωオートマトンは次の要素から構成される タプルA = ( Q ,Σ,δ, q 0 , Acc )です。
- Qは有限集合である。Q の元はAの状態と呼ばれる。
- Σ はAのアルファベットと呼ばれる有限集合です。
- δ: Q × Σ → QはAの遷移関数と呼ばれる関数です。
- q 0はQの要素であり、初期状態と呼ばれます。
- Accは受入れ条件であり、正式にはQ ωのサブセットです。
Aへの入力はアルファベットΣ上の無限列、すなわち無限列α = ( a 1 , a 2 , a 3 ,...)である。このような入力に対するAの連続は、以下のように定義される状態の無限列ρ = ( r 0 , r 1 , r 2 ,...)である。
- r 0 = q 0 です。
- r 1 = δ( r 0 , a 1 )。
- r 2 = δ( r 1 , a 2 ) です。
- ...
- つまり、すべてのiについて:r i = δ( r i -1 , ai )。
ω-オートマトンの主な目的は、すべての入力集合のサブセット、すなわち受理される入力集合を定義することです。通常の有限オートマトンの場合、すべての実行は状態r nで終了し、 r n が受理状態である場合にのみ入力が受理されますが、ω-オートマトンの場合、受理される入力集合の定義はより複雑です。ここでは、実行ρ全体を検討する必要があります。対応する実行がAccにある場合、入力は受理されます。受理される入力ω語の集合は、オートマトンによって 認識されるω言語と呼ばれ、L(A)と表記されます。
AccをQ ωの部分集合として定義することは、純粋に形式的なものであり、通常そのような集合は無限であるため、実用には適していません。様々な種類の ω オートマトン(Büchi、Rabin など)の違いは、Q ωの特定の部分集合Acc を有限集合としてどのように符号化するか、つまりどの部分集合を符号化できるかにあります。
非決定性ωオートマトン
正式には、非決定性ωオートマトンは次の要素から構成される タプルA = ( Q ,Σ,Δ, Q 0 , Acc )です。
- Qは有限集合である。Q の元はAの状態と呼ばれる。
- Σ はAのアルファベットと呼ばれる有限集合です。
- Δ はQ × Σ × Qのサブセットであり、 Aの遷移関係と呼ばれます。
- Q 0はQのサブセットであり、初期状態セットと呼ばれます。
- AccはQ ωのサブセットである受入れ条件です。
遷移関数 δ を持つ決定性ωオートマトンとは異なり、非決定性版は遷移関係 Δ を持つ。Δ は 、 Q × Σから冪集合P ( Q ) への関数 : Q × Σ → P ( Q ) とみなせることに注意されたい。したがって、状態q nとシンボルa nが与えられた場合、次の状態q n +1は必ずしも一意に決定されるわけではなく、むしろ次の状態の集合が存在する。
入力 α = ( a 1 , a 2 , a 3 ,...) に対するAの実行は、次の条件を満たす状態の 無限シーケンス ρ = ( r 0 , r 1 , r 2 ,...) です。
- r 0はQ 0の要素です。
- r 1はΔ( r 0 , a 1 )の要素である。
- r 2はΔ( r 1 , a 2 )の要素である。
- ...
- つまり、すべてのi : r iはΔ( r i -1 , ai )の要素です。
非決定性ω-オートマトンでは、与えられた入力に対して複数の異なる実行を許容することも、全く実行を許容しないこともあります。入力は、可能な実行のうち少なくとも1つが受理可能である場合に受理されます。実行が受理可能かどうかは、決定性ω-オートマトンと同様に、 Accのみに依存します。Δ を δ のグラフとすることで、すべての決定性ω-オートマトンを非決定性ω-オートマトンと見なすことができます。したがって、決定性ω-オートマトンにおける実行と受理の定義は、非決定性の場合の特別なケースとなります。
受諾条件
受容条件はω語の無限集合となる場合があります。しかし、研究される受容条件は有限表現可能なものがほとんどです。以下に、一般的な受容条件をいくつか挙げます。
リストについて議論する前に、次の点について考察しておきましょう。無限に実行されるシステムの場合、特定の動作が無限に繰り返されるかどうかがしばしば関心の対象となります。例えば、ネットワークカードが無限に多くのping要求を受信した場合、一部の要求には応答しない可能性がありますが、受信したping要求の無限個のサブセットには応答する必要があります。このことから、次の定義が導き出されます。任意の実行ρについて、ρ内で無限に発生する状態の集合をInf(ρ)とします。特定の状態が無限に訪れるというこの概念は、以下の受け入れ条件を定義する際に役立ちます。
- Büchiオートマトンとは、 Qの何らかのサブセットFに対して次の受理条件を使用するωオートマトンAである。
- ビュッヒ条件
- Aは、Inf(ρ) ∩Fが空ではない実行ρを正確に受け入れます 。つまり、ρには無限に頻繁に発生する受け入れ状態があります。
- あラビンオートマトンとは、状態集合のペア(B i、G i )の集合Ωに対して以下の受理条件を用いるωオートマトンA
- ラビン条件
- Aは、B i ∩ Inf(ρ)が空でG i ∩ Inf(ρ)が空ではないような、Ω内にペア(B i、G i )が存在するような実行ρだけを受け入れます 。
- ストリートオートマトンとは、状態集合のペア(B i、G i )の集合Ωに対して次の受理条件を使用するωオートマトンAである。
- 路面状況
- Aは、Ω内のすべてのペア(B i、G i )について、B i ∩ Inf(ρ)が空でないか、G i ∩ Inf(ρ)が空であるような実行ρを正確に受け入れ ます。
- パリティオートマトンとは、ある自然数 kに対して状態の集合がQ = {0,1,2,..., k } であるオートマトンAであり、次の受入れ条件を満たすものです。
- パリティ条件
- Aは、Inf(ρ)の最小の数が偶数である場合にのみρを受け入れます。
- ミュラー条件
- Aは、 Inf(ρ)がFの要素となる実行ρだけを受け入れます 。
全てのビュッヒ・オートマトン( Büchi automaton)はミュラー・オートマトンとみなすことができます。Qの少なくとも1つの要素を含む 部分集合F ' をFに置き換えるだけで十分です。同様に、全てのラビン・オートマトン、ストリート・オートマトン、またはパリティ・オートマトンもミュラー・オートマトンとみなすことができます。
例
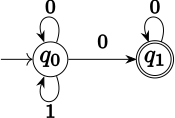
アルファベット Σ = {0,1} 上の 次の ω 言語L は、非決定性 Büchi オートマトンによって認識できます。L は、1 が有限回しか出現しない Σ ωのすべての ω ワードで構成されます。Lを認識する非決定性 Büchi オートマトンには、q 0 (初期状態) とq 1の2 つの状態のみが必要です。Δ は、3 つの組 ( q 0 ,0, q 0 )、 ( q 0 ,1, q 0 )、 ( q 0 ,0, q 1 )、および ( q 1 ,0, q 1 ) で構成されます。F = { q 1 } 。1が有限回しか出現しない任意の入力 α に対して、読み取る 1 がある限り状態q 0に留まり、その後状態q 1に移行する実行が存在します。この実行は成功です。 1 が無限に存在する場合、実行可能な実行は 1 つだけです。つまり、常に状態q 0に留まる実行です。(マシンがq 0を離れてq 1に到達すると、戻ることはできません。別の 1 が読み取られた場合、後続の状態はありません。)
上記の言語は、非決定的なオートマトンよりも 表現力が劣る決定的なBüchi オートマトンでは認識できないことに注意してください。
ω-オートマトンの表現力
有限アルファベット Σ 上の ω-言語は、 Σ 上の ω-単語の集合、すなわち Σ ωの部分集合である。Σ 上の ω-言語が、 ω-オートマトンA (同じアルファベットを持つ)によって認識されるとは、それがAが受け入れるすべての ω-単語の集合であることを意味する。ω-オートマトンのあるクラスの表現力は、そのクラス内のいずれかのオートマトンが認識できるすべての ω-言語のクラスによって測られる。
非決定性ビュッヒ、パリティ、ラビン、ストリート、ミュラーのオートマトンはすべて、全く同じω-言語のクラスを認識します。[1] これらは、正規言語のω-クリーネ閉包、または正規ω-言語として知られています。異なる証明を用いて、決定性パリティ、ラビン、ストリート、ミュラーのオートマトンはすべて正規ω-言語を認識することも示せます。このことから、正規ω-言語のクラスは補集合に関して閉じていることがわかります。しかし、上記の例は、決定性ビュッヒのオートマトンが厳密に弱いことを示しています。
ω-automata間の変換
非決定性ミュラー、ラビン、ストリート、パリティ、そしてビュッヒのオートマトンは同じ表現力を持つため、相互に翻訳可能です。以下の略語を用いましょう。例えば、NBは非決定性ビュッヒωオートマトン、DPは決定性パリティωオートマトンを表します。すると、以下の式が成り立ちます。
- 明らかに、あらゆる決定論的オートマトンを非決定論的オートマトンとして見ることができます。
- 状態空間での爆発はありません。
- 状態空間における多項式爆発、すなわち結果として得られるNBの状態数は であり、ここではNBの状態数、 はラビン受容ペアの数である(例えば、[2]を参照)。
- 状態空間で指数関数的に増加します。
- 状態空間において指数関数的な爆発を伴います。この決定論的結果はサフラの構成を用いています。
翻訳の包括的な概要は、参照されているウェブソースで見つけることができます。[3]
決定可能性への応用
ω-オートマトンを用いて、後継者の下での自然数の モナディック2階理論(MSO)であるS1Sの決定可能性を証明することができます。無限木オートマトンはω-オートマトンを無限木に拡張し、 2つの後継者を持つMSO理論であるS2Sの決定可能性を証明するために使用できます。また、これは、木幅が制限された(固定された境界が与えられた)グラフのMSO理論にも拡張できます。
さらに読む
- Farwer、Berndt (2002)、「ω-Automata」、Grädel、Erich。トーマス、ヴォルフガング。 Wilke, Thomas (編)、『Automata, Logics, and Infinite Games』、Lecture Notes in Computer Science、Springer、pp. 3–21、ISBN 978-3-540-00388-5。
- ペラン、ドミニク、ピン、ジャン=エリック(2004)、Infinite Words:オートマトン、半群、論理とゲーム、エルゼビア、ISBN 978-0-12-532111-2
- Thomas, Wolfgang (1990)、「無限物体上のオートマトン」、Jan van Leeuwen (編)、『理論計算機科学ハンドブック』第B巻、MIT Press、pp. 133– 191、ISBN 978-0-262-22039-2
- Bakhadyr Khoussainov、Anil Nerode(2012年12月6日)『オートマトン理論とその応用』Springer Science & Business Media. ISBN 978-1-4612-0171-7。
参考文献
- ^ Safra, S. (1988)、「ω-オートマトンにおける複雑性について」、第29回コンピュータサイエンスの基礎に関する年次シンポジウム(FOCS '88)の議事録、ワシントン DC、米国: IEEE コンピュータ協会、pp. 319– 327、doi :10.1109/SFCS.1988.21948。
- ^ Esparza, Javier (2017)、「オートマトン理論:アルゴリズム的アプローチ」(PDF)
- ^ Boker, Udi (2018年4月18日). 「Word-Automata Translations」. Udi Bokerのウェブページ. 2019年3月30日閲覧。







