ホイットニー傘

表面の断面

幾何学において、ホイットニーの傘（ホイットニーの傘）は、アメリカの数学者ハスラー・ホイットニーにちなんで名付けられ、ケーリーの傘とも呼ばれる、三次元上に配置された特定の自己交差する線織面である。これは、固定放物線の点を通り、放物線の軸に平行でその垂直二等分面上にある固定直線に垂直なすべての直線の和集合である。

数式

ホイットニーの傘は直交座標の媒介変数方程式で表すことができる。

${\displaystyle \left\{{\begin{aligned}x(u,v)&=uv,\\y(u,v)&=u,\\z(u,v)&=v^{2},\end{aligned}}\right.}$

ここで、パラメータuとvは実数の範囲である。これはまた、次の暗黙の方程式によっても与えられる。

${\displaystyle x^{2}-y^{2}z=0.}$

この式には、負のZ軸 (傘の 柄と呼ばれる) も含まれます。

プロパティ

動く直線によって生成される線織面としてのホイットニー傘

プラスチックの立方体の中に一本の紐で作られたホイットニー傘

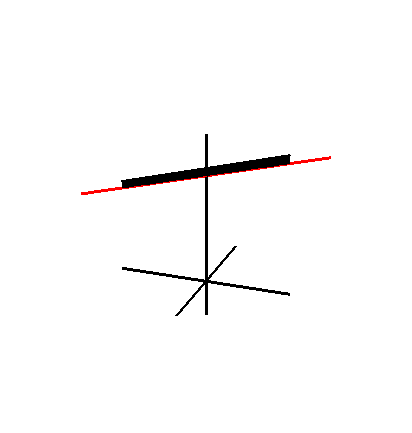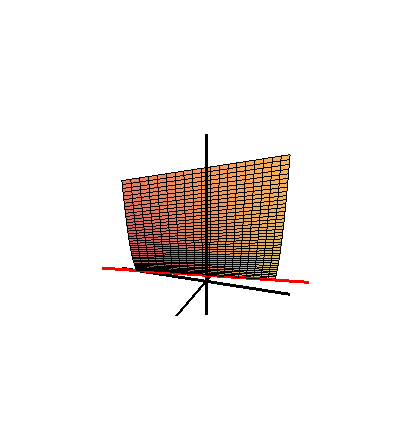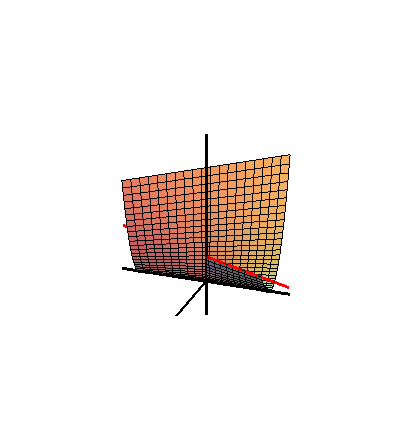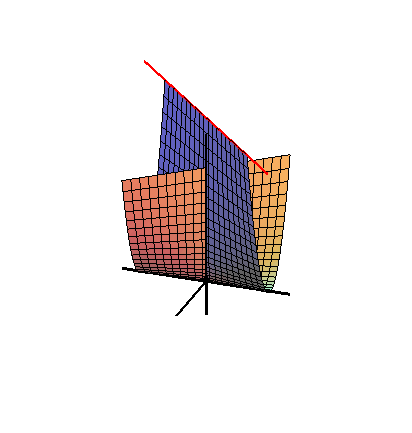
ホイットニーの傘は、線織面と直円錐面から成ります。特異点理論の分野では、ピンチポイント特異点の単純な局所モデルとして重要です。ピンチポイント特異点と褶曲特異点は、 R ^2からR ³への写像における唯一の安定な局所特異点です。

アメリカの 数学者 ハスラー・ホイットニーにちなんで名付けられました。

弦理論において、ホイットニー・ブレーンとは、特異点が局所的にホイットニー・アンブレラによってモデル化される多様体を包むD7ブレーンである。ホイットニー・ブレーンは、F理論におけるセンの弱結合極限をとることで自然に現れる。

参照

• クロスキャップ
• 右円錐
• 罫線面

参考文献

• 「ホイットニーの傘」。位相幾何学動物園。幾何学センター。 2006年3月8日閲覧。（ホイットニー傘の画像と動画）