非対称グラフ

非自明な対称性を持たない無向グラフ

数学の一分野であるグラフ理論では、無向グラフが非自明な対称性を持たない場合、非対称グラフと呼ばれます。

正式には、グラフの自己同型とは、任意の2つの頂点 $u$ と $v$ が隣接する場合と、 $p$ $($ $u$ $)$ と $p$ $($ $v$ $)$ が隣接する場合に限り、その頂点の順列 $p$ である。グラフの恒等写像は常に自己同型であり、グラフの自明な自己同型と呼ばれる。非対称グラフとは、他に自己同型が存在しないグラフである。

「非対称グラフ」という用語は「対称グラフ」という用語の否定ではないことに注意してください。後者は、非自明な対称性を持つことよりも強い条件を指します。

例

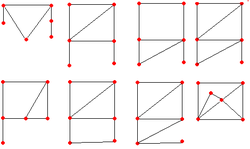
最小の非対称非自明グラフは 6 頂点を持つ。^[1]最小の非対称正則グラフは10 頂点を持つ。4正則と5 正則の10 頂点非対称グラフも存在する。^[2]^[3]最小の 5 つの非対称立方グラフ^[4]の 1 つは、 1939 年に発見された12 頂点のFrucht グラフである。 ^[5]Frucht の定理の強化版によれば、非対称立方グラフは無限に存在する。

プロパティ

非対称グラフのクラスは補グラフに関して閉じている。つまり、グラフGが非対称であるのは、その補グラフが非対称である場合に限る。^[1]n頂点の非対称グラフは、最大でn /2 + o( n )本の辺を追加または削除することで対称にすることができる。^[1]

ランダムグラフ

n頂点のグラフのうち、非自明な自己同型性を持つものの割合は、 nが増加するにつれてゼロに近づく。これは非公式には「ほぼすべての有限グラフは非対称である」と表現される。対照的に、これも非公式には「ほぼすべての無限グラフは非自明な対称性を持つ」と表現される。より具体的には、エルデシュ・レーニイモデルにおける可算無限ランダムグラフは、確率1で、高度に対称的なラドグラフと同型である。^[1]

木々

最小の非対称木は7つの頂点を持ち、長さ1、2、3の3つのパスが共通の端点で結ばれた構造をしています。^[6]グラフの場合とは対照的に、ほとんどすべての木は対称的です。特に、n個のラベル付きノードを持つすべての木の中から一様にランダムに木を選択した場合、 nが増加するにつれて確率が1に近づくにつれて、その木には同じノードに隣接する2つの葉が含まれ、これらの2つの葉を交換する対称性があります。^[1]

参考文献

^ abcde エルデシュ、P. ; Rényi, A. (1963)、「非対称グラフ」、Acta Mathematica Hungarica、14 (3): 295–315、doi : 10.1007/BF01895716。
^ バロン、G. Imrich, W. (1969)、「Asymmetrische reguläre Graphen」、Acta Mathematica Academiae Scientiarum Hungaricae、20 ( 1–2 ): 135–142、doi : 10.1007/BF01894574、MR 0238726。
^ アラン・ゲヴィルツ;ヒル、アンソニー。 Quintas、Louis V. (1969)、「正則非対称グラフの最小点数」、フェデリコサンタマリア工科大学。サイエンティア、138 : 103–111、MR 0266818。
^ Bussemaker, FC; Cobeljic, S.; Cvetkovic, DM; Seidel, JJ (1976), 立方グラフのコンピュータ調査、EUTレポート、vol. 76-WSK-01、アイントホーフェン工科大学数学・計算科学科
^ Frucht, R. (1939)、「Herstellung von Graphen mit vorgegebener abstrakter Gruppe.」、Compositio Mathematica (ドイツ語)、6 : 239–250、ISSN 0010-437X、Zbl 0020.07804 。
^ Quintas, Louis V. (1967)、「非対称グラフに関する極値」、Journal of Combinatorial Theory、3 (1): 57– 82、doi : 10.1016/S0021-9800(67)80018-8。

[er63-1] エルデシュ、P. ; Rényi, A. (1963)、「非対称グラフ」、Acta Mathematica Hungarica、14 (3): 295–315、doi : 10.1007/BF01895716。

[2] バロン、G. Imrich, W. (1969)、「Asymmetrische reguläre Graphen」、Acta Mathematica Academiae Scientiarum Hungaricae、20 ( 1–2 ): 135–142、doi : 10.1007/BF01894574、MR 0238726。

[3] アラン・ゲヴィルツ;ヒル、アンソニー。 Quintas、Louis V. (1969)、「正則非対称グラフの最小点数」、フェデリコサンタマリア工科大学。サイエンティア、138 : 103–111、MR 0266818。

[4] Bussemaker, FC; Cobeljic, S.; Cvetkovic, DM; Seidel, JJ (1976), 立方グラフのコンピュータ調査、EUTレポート、vol. 76-WSK-01、アイントホーフェン工科大学数学・計算科学科

[f39-5] Frucht, R. (1939)、「Herstellung von Graphen mit vorgegebener abstrakter Gruppe.」、Compositio Mathematica (ドイツ語)、6 : 239–250、ISSN 0010-437X、Zbl 0020.07804 。

[6] Quintas, Louis V. (1967)、「非対称グラフに関する極値」、Journal of Combinatorial Theory、3 (1): 57– 82、doi : 10.1016/S0021-9800(67)80018-8。

自己同型によって定義されるグラフ族
距離推移	→	距離レギュラー	←	強く規則的な
↓
対称的（弧推移的）	←	t推移的、 $t \geq 2$		歪対称
↓
_{（接続されている場合）} 頂点および辺が推移的	→	エッジ推移的かつ正則	→	エッジ推移的
↓		↓		↓
頂点推移	→	通常	→	_{（二部構成の場合）} 双正則
↑
ケイリーグラフ	←	ゼロ対称		非対称