チェーン錯体

数学において、鎖複体とは、アーベル群（または加群）の列と、連続する群間の準同型の列から成り、各準同型の像が次の準同型の核に含まれる代数構造です。鎖複体にはホモロジーが関連しており、これは（大まかに言えば）鎖複体が正確ではないことの尺度です。

コチェーン複体は、準同型が反対方向にあることを除いて、鎖複体に似ています。コチェーン複体のホモロジーは、コホモロジーと呼ばれます。

代数的位相幾何学において、位相空間Xの特異鎖複体は、単体からXへの連続写像を用いて構築され、鎖複体の準同型は、これらの写像が単体の境界にどのように制限されるかを捉えます。この鎖複体のホモロジーは、 Xの特異ホモロジーと呼ばれ、位相空間の よく使われる不変量です

連鎖複体はホモロジー代数学で研究されていますが、抽象代数学、ガロア理論、微分幾何学、代数幾何学など、数学のいくつかの分野で使用されています。 より一般的にはアーベル圏で定義できます

定義

連鎖複体とは、準同型（ 境界作用素または微分と呼ばれる）で接続されたアーベル群または加群の列であり、任意の2つの連続する写像の合成は零写像となる。明示的には、微分はすべてのに対してを満たす。簡潔には、である。この複体は次のように表記できる。 ${\displaystyle (A_{\bullet },d_{\bullet })}$ ${\displaystyle \cdots ,A_{0},A_{1},A_{2},\dots }$ ${\displaystyle d_{n}:A_{n}\to A_{n-1}}$ ${\displaystyle d_{n}\circ d_{n+1}=0}$ ${\displaystyle n}$ ${\displaystyle d^{2}=0}$

${\displaystyle \cdots \xleftarrow {d_{0}} A_{0}\xleftarrow {d_{1}} A_{1}\xleftarrow {d_{2}} A_{2}\xleftarrow {d_{3}} A_{3}\xleftarrow {d_{4}} A_{4}\xleftarrow {d_{5}} \cdots }$

コチェーン複体は、連鎖複体の 双対概念である。これは、準同型（共境界作用素）で接続され、を満たすアーベル群または加群の列から構成される。コチェーン複体は、連鎖複体と同様の方法で表記できる ${\displaystyle (A^{\bullet },d^{\bullet })}$ ${\displaystyle \cdots ,A^{0},A^{1},A^{2},\dots }$ ${\displaystyle d^{n}:A^{n}\to A^{n+1}}$ ${\displaystyle d^{n+1}\circ d^{n}=0}$

${\displaystyle \cdots \xrightarrow {d^{-1}} A^{0}\xrightarrow {d^{0}} A^{1}\xrightarrow {d^{1}} A^{2}\xrightarrow {d^{2}} A^{3}\xrightarrow {d^{3}} A^{4}\xrightarrow {d^{4}} \cdots }$

どちらの場合も、指数は次数（または次元）と呼ばれます。連鎖複体と共連鎖複体の違いは、連鎖複体では微分によって次元が減少するのに対し、共連鎖複体では微分によって次元が増加することです。連鎖複体の概念と定義はすべて共連鎖複体にも適用されますが、次元についてはこの異なる規則に従い、多くの場合、用語には接頭辞co-が付けられます。この記事では、区別が不要な場合は連鎖複体の定義を示します。 ${\displaystyle n}$

有界連鎖複体とは、ほぼすべてのが0である複体です。つまり、有限複体を左右に0だけ拡張したものです。例としては、有限単体複体の単体ホモロジーを定義する連鎖複体があります。ある固定次数より上のすべてのモジュールが0の場合、連鎖複体は上方に有界であり、ある固定次数より下のすべてのモジュールが0の場合、連鎖複体は下方に有界です。明らかに、複体が上方と下方の両方に有界なのは、複体が有界な場合のみです ${\displaystyle A_{n}}$ ${\displaystyle N}$

（コ）チェイン複体の個々の群の元は（コ）チェインと呼ばれます。の核の元は（コ）サイクル（または閉元）と呼ばれ、 dの像の元は（コ）境界（または正確な元）と呼ばれます。微分の定義から、すべての境界はサイクルです。n次（コ）ホモロジー群H _n ( H ⁿ )は、n次の（コ）境界を法とする（コ）サイクルの群です。つまり、 ${\displaystyle d}$

${\displaystyle H_{n}=\ker d_{n}/{\mbox{im }}d_{n+1}\quad \left(H^{n}=\ker d^{n}/{\mbox{im }}d^{n-1}\right)}$

正確な配列

完全列（または完全複体）は、ホモロジー群がすべてゼロである鎖複体です。これは、複体内のすべての閉元が完全であることを意味します。短完全列は、群A _k、A _{k +1}、A _{k +2}のみが非ゼロになり得る、有界完全列です。例えば、次の鎖複体は短完全列です。

${\displaystyle \cdots {\xrightarrow {}}\;0\;{\xrightarrow {}}\;\mathbf {Z} \;{\xrightarrow {\times p}}\;\mathbf {Z} \twoheadrightarrow \mathbf {Z} /p\mathbf {Z} \;{\xrightarrow {}}\;0\;{\xrightarrow {}}\cdots }$

中央の群では、閉元は元 p Zです。これらは明らかにこの群の完全元です。

鎖写像

2つの鎖複体と鎖写像 f は、2つの鎖複体上の境界 作用素と可換な各nに対する準同型の列です。つまり、 です。これは次の可換図で表されます。 ${\displaystyle (A_{\bullet },d_{A,\bullet })}$ ${\displaystyle (B_{\bullet },d_{B,\bullet })}$ ${\displaystyle f_{\bullet }}$ ${\displaystyle f_{n}:A_{n}\rightarrow B_{n}}$ ${\displaystyle d_{B,n}\circ f_{n}=f_{n-1}\circ d_{A,n}}$

鎖写像は、サイクルをサイクルに、境界を境界に送り、それによってホモロジー 上の写像を誘導します ${\displaystyle (f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })}$

位相空間XとYの間の連続写像f は、 XとYの特異鎖複体間の鎖写像を誘導し、したがって、XとYの特異ホモロジー間の写像f _*も誘導します。XとYが両方ともn次元球面に等しい場合、ホモロジー上に誘導される写像は写像fの次数を定義します。

鎖写像の概念は、鎖写像の 錐の構築を通じて境界の概念に還元されます。

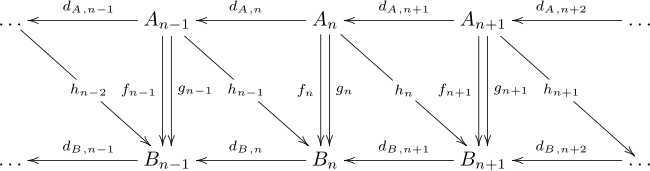
鎖ホモトピー

連鎖ホモトピーは、ホモロジー群上に同じ写像を誘導する2つの連鎖写像を、たとえ写像が異なっていても関連付ける方法を提供する。2つの連鎖複体AとB、および2つの連鎖写像f , g  : A → Bが与えられたとき、連鎖ホモトピーとは、 hd _A + d _B h = f − gを満たす準同型写像h _n  : A _n → B _{n +1}の列である。これらの写像は次のように図式化できるが、この図は可換ではない。

写像hd _A + d _B h は、任意のhに対して、ホモロジー上の零写像を誘導することが容易に証明されます。fとg はホモロジー上に同じ写像を誘導することが直ちに示されます。fとgは連鎖ホモトピック（または単にホモトピック）であると言い、この性質は連鎖写像間の 同値関係を定義します。

XとYを位相空間とします。特異ホモロジーの場合、連続写像f , g  : X → Y間のホモトピーは、 fとgに対応する連鎖写像間の連鎖ホモトピーを誘導します。これは、2つのホモトピック写像が特異ホモロジー上に同じ写像を誘導することを示しています。「連鎖ホモトピー」という名前はこの例に由来しています。

例

特異ホモロジー

X を位相空間とします。自然nに対してC _n ( X ) をX内の特異 n 単体によって形式的に生成される自由アーベル群と定義し、境界写像を次のように 定義します ${\displaystyle \partial _{n}:C_{n}(X)\to C_{n-1}(X)}$

${\displaystyle \partial _{n}:\,(\sigma :[v_{0},\ldots ,v_{n}]\to X)\mapsto (\sum _{i=0}^{n}(-1)^{i}\sigma :[v_{0},\ldots ,{\hat {v}}_{i},\ldots ,v_{n}]\to X)}$

ここで、ハットは頂点の省略を表します。つまり、特異単体の境界は、その面への制約の交代和です。∂ ² = 0 であることが示され、連鎖複体も同様です。特異ホモロジーは、この複体のホモロジーです。 ${\displaystyle (C_{\bullet },\partial _{\bullet })}$ ${\displaystyle H_{\bullet }(X)}$

特異ホモロジーは、ホモトピー同値を除き、位相空間の有用な不変量です。次数ゼロのホモロジー群は、Xのパス成分上の自由アーベル群です。

ド・ラーム・コホモロジー

任意の滑らかな多様体M 上の微分k形式は、加法の下でΩ ^k ( M )と呼ばれる実ベクトル空間を形成する。外微分dは Ω ^k ( M ) を Ω ^{k +1} ( M ) に写し、d ² = 0 は本質的に二階微分の対称性から導かれる。したがって、k形式のベクトル空間と外微分は共鎖複素となる。

${\displaystyle 0{\stackrel {\subset }{\to }}\ {\Re ^{c}}{\stackrel {\subset }{\to }}\ {\Omega ^{0}(M)}{\stackrel {d}{\to }}\ {\Omega ^{1}(M)}{\stackrel {d}{\to }}\ {\Omega ^{2}(M)}{\stackrel {d}{\to }}\ \Omega ^{3}(M)\to \cdots }$

この複体のコホモロジーは、Mのde Rham コホモロジーと呼ばれます。局所定数関数は、 Mの互いに分離した成分の数 c との同型で表されます。このようにして、複体は部分集合作用素を用いて零形式レベルで複体を正確に保つように拡張されました。 ${\displaystyle \Re ^{c}}$

多様体間の滑らかな写像は連鎖写像を誘導し、写像間の滑らかなホモトピーは連鎖ホモトピーを誘導します。

鎖状錯体のカテゴリ

射として連鎖写像を持つ -加群の連鎖複体は、圏を形成します。ここで は可換環です。 ${\displaystyle K}$ ${\displaystyle \mathbf {Ch} _{K}}$ ${\displaystyle K}$

と が連鎖複体である場合、それらのテンソル積は、次数元が で与えられる 連鎖複体です。${\displaystyle V=V_{*}}$ ${\displaystyle W=W_{*}}$ ${\displaystyle V\otimes W}$ ${\displaystyle n}$

${\displaystyle (V\otimes W)_{n}=\bigoplus _{\{i,j\mid i+j=n\}}V_{i}\otimes W_{j}}$

および微分が で与えられます。

${\displaystyle \partial (a\otimes b)=\partial a\otimes b+(-1)^{\left|a\right|}a\otimes \partial b}$

ここで、 とはそれぞれと の任意の2つの同次ベクトルであり、の 次数を表します${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle V}$ ${\displaystyle W}$ ${\displaystyle \left|a\right|}$ ${\displaystyle a}$

このテンソル積は、カテゴリを対称モノイドカテゴリにします。このモノイド積に関する恒等対象は、次数 の鎖複体として見た基本環です。編組は、同次元の単純テンソル上で次のように与えられます。 ${\displaystyle \mathbf {Ch} _{K}}$ ${\displaystyle K}$ ${\displaystyle 0}$

${\displaystyle a\otimes b\mapsto (-1)^{\left|a\right|\left|b\right|}b\otimes a}$

編組が鎖写像になるためには、符号が必要です。

さらに、 -加群の鎖複体のカテゴリも内部Homを持ちます。鎖複体とが与えられた場合、との内部Hom（と表記）は、次数元が で与えられ、微分が で与えられる 鎖複体です。${\displaystyle K}$ ${\displaystyle V}$ ${\displaystyle W}$ ${\displaystyle V}$ ${\displaystyle W}$ ${\displaystyle \mathrm {Hom} (V,W)}$ ${\displaystyle n}$ ${\displaystyle \Pi _{i}{\text{Hom}}_{K}(V_{i},W_{i+n})}$

${\displaystyle (\partial f)(v)=\partial (f(v))-(-1)^{\left|f\right|}f(\partial (v))}$ 。

自然同型が成り立ちます。

${\displaystyle {\text{Hom}}(A\otimes B,C)\cong {\text{Hom}}(A,{\text{Hom}}(B,C))}$

その他の例

• アミチュール複体
• ブロッホの高次チョウ群を定義するために使用される複体
• ブックスバウム・リム複体
• チェフ複体
• カズン複体
• イーゴン・ノースコット複体
• ゲルステン複体
• グラフ複体^[1]
• コズル複体
• ムーア複体
• シューア複体

参照

• 微分次数代数
• 微分次数リー代数
• ドルド・カン対応によれば、連鎖複体の圏と単体アーベル群の圏の間には同値性がある。
• ブックスバウム・アイゼンバッド非巡回性基準
• 微分次数加群

参考文献

1. 「グラフ複素数」

• ボット、ラウル；トゥ、ローリング W. (1982)、『代数的位相幾何学における微分形式』、ベルリン、ニューヨーク：シュプリンガー・フェアラーク、ISBN 978-0-387-90613-3
• ハッチャー、アレン(2002)、『代数的位相幾何学』、ケンブリッジ：ケンブリッジ大学出版局、ISBN 0-521-79540-0。