ダイラタンシー（粒状物質）

密な砂におけるひずみの関数としての応力差の典型的な曲線。

土質力学において、ダイラタンシーまたは剪断ダイラタンシー^[1]とは、粒状材料が剪断変形を受けた際に観察される体積変化である^{[2] [3]}。この効果は、 1885年または1886年にオズボーン・レイノルズによって初めて科学的に記述され^{[4] [5] 、}レイノルズ・ダイラタンシーとしても知られている。この現象は、ピーター・ウォルター・ロウ [de]によって土質工学分野に導入された^[6]。

他のほとんどの固体材料とは異なり、圧縮された高密度粒状物質はせん断を受けると膨張（体積が膨張）する傾向があります。これは、圧縮状態の粒子が互いに絡み合っているため、互いに自由に動き回ることができないためです。応力を受けると、隣接する粒子間にてこ運動が生じ、物質の体積膨張を引き起こします。一方、粒状物質が非常に緩い状態から始まる場合、せん断を受けて膨張するのではなく、継続的に圧縮される可能性があります。ある物質のサンプルは、せん断の増加に伴って体積が増加する場合、膨張型と呼ばれます。また、せん断の増加に伴って体積が減少する場合、収縮型と呼ばれます。[ 7 ] ^{[ 8]}

ダイラタンシーは土壌や砂に共通する特性です。その影響は、海岸を歩く人の足元の湿った砂が乾いたように見えることで確認できます。足による変形によって砂が膨張し、砂の中の水分が移動して砂粒間の新たな空間を埋めます。

現象

単純せん断における高密度砂サンプルのダイラタンシー。

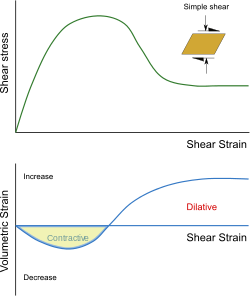
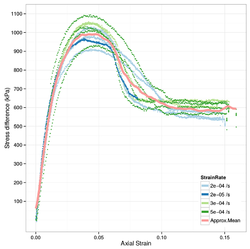
ダイラタンシー現象は、密な砂のサンプルを用いた排水単純せん断試験で観察されます。変形の初期段階では、せん断ひずみが増加するにつれて体積ひずみが減少します。しかし、応力がピーク値に近づくと、体積ひずみは増加し始めます。さらにせん断が進むと、土サンプルの体積は試験開始時よりも大きくなります。

膨張量は土壌の初期密度に大きく依存します。一般的に、土壌の密度が高いほど、せん断による体積膨張量が大きくなります。また、有効垂直応力が減少すると内部摩擦角が減少することも観察されています。^[9]

膨張と内部摩擦の関係は、典型的には鋸歯状ダイラタンシーモデルによって説明される。このモデルでは、膨張角は鋸歯が水平面に対してなす角度と類似している。このモデルを用いることで、観測される摩擦角は、膨張角と膨張ゼロ時の摩擦角の和に等しいと推論することができる。^[要出典]

意義

ダイラタンシーの影響により、摩擦角は拘束が増加するにつれて増加し、ピーク値に達します。土のピーク強度が上昇した後、摩擦角は急激に減少します。そのため、このような土質における斜面、フーチング、トンネル、杭などの土質工学においては、土質強度がこのピーク値に達した後の潜在的な強度低下を考慮する必要があります。

微量の砂から砂質を含む、非塑性で分級の不十分な/均一なシルトは、硬くても建設中に問題を引き起こす可能性があります。これらの材料は、シルトが非常に粗いため粒状に見えることが多く、そのため高密度から非常に高密度と説明される場合があります。これらの土質における地下水位より下の垂直掘削は、マトリック吸引の影響もあって、多くの高密度砂質土堆積物と同様に短期的な安定を示します。しかし、重力によりアクティブウェッジ内で土壌のせん断が発生すると、強度が失われ、破壊速度が加速します。この状況は、アクティブウェッジの背面付近の張力亀裂に水が集まる場所で静水力が発生することで悪化する可能性があります。一般的に後退的な剥離が現れ、パイピング/内部侵食を伴うことがよくあります。これらの材料を管理するには、適切なフィルターの使用が重要です。好ましいフィルターとしては、市販の骨材として一般的に入手しやすい#4サイズの透明な砂利または粗粒砂が挙げられます。不織布フィルターも適しています。他のフィルターと同様に、D15およびD50の適合基準を確認してください。

ダイラタンシーカットオフ

広範囲のせん断を受けた膨張性材料は、ダイラタンシーが限界に達した臨界密度状態に達する。この土質挙動は、ダイラタンシーのカットオフを用いることで硬化土モデルに組み込むことができる。この挙動を規定するためには、材料の初期空隙比と最大空隙比 を一般パラメータとして入力する必要がある。体積変化によって最大空隙状態に達すると、移動ダイラタンシー角 は自動的にゼロに戻される。^[10]${\displaystyle e_{init}}$ ${\displaystyle e_{max}}$ ${\displaystyle \psi_{m}}$

参照

• 三軸せん断試験
• μ(I)レオロジー：粒状流のレオロジーの1つのモデル。

参考文献

1. Tighe, Brian P. (2014年4月). 「境界固体におけるせん断ダイラタンシー」. Granular Matter . 16 (2): 203– 208. arXiv : 1305.5574 . doi :10.1007/s10035-013-0436-6.
2. Nedderman, RM (1992).粒状材料の静力学と運動学. doi :10.1017/CBO9780511600043. ISBN 978-0-521-40435-8。^{[ページが必要]}
3. アンドレオッティ、ブルーノ;フォルテール、ヨエル。オリヴィエ・プリカン (2013)。粒状媒体: 流体と固体の間。ケンブリッジ大学出版局。ISBN 978-1-107-03479-2。^{[ページが必要]}
4. レイノルズ、オズボーン（1885年12月）「LVII. 接触する剛体粒子からなる媒質のダイラタンシーについて。実験例付き」ロンドン、エディンバラ、ダブリン哲学雑誌・科学ジャーナル20 ( 127): 469– 481. doi :10.1080/14786448508627791.
5. レイノルズ、オズボーン（1886年2月12日）。「重力と関連している可能性のある粒状物質の特性、ダイラタンシーを示す実験」英国王立協会。毎週夕方の会合。OCLC 1440246508  。
6. Rowe, PW (1962年10月9日). 「接触粒子集合体の静的平衡における応力-ダイラタンシー関係」.ロンドン王立協会紀要. シリーズA. 数学・物理科学. 269 (1339): 500– 527. Bibcode :1962RSPSA.269..500R. doi :10.1098/rspa.1962.0193.
7. Casagrande, A., Hirschfeld, RC, Poulos, SJ (1964). 第4報：圧縮粘土の応力-変形および強度特性の調査. ハーバード大学ケンブリッジ校 MA土質力学研究室.
8. Poulos, SJ (1971). 土壌の応力-ひずみ曲線. Geotechnical Engineers Incorporated. シカゴ.
9. Houlsby, GT (1991年5月28日). 土壌のダイラタンシーが土の挙動に与える影響(PDF) . 第10回ヨーロッパ土質力学・基礎工学会議. フィレンツェ, イタリア. Bibcode :1991smfe.conf.....H.
10. PLAXIS 2D CE V20.02: 3 - 材料モデルマニュアル.pdf 78ページ^{[全文引用が必要]}