リンク/カットツリー

リンク/カットツリー
リンク/カットツリー
タイプ	木
発明された	1982
発明者	ダニエル・ドミニク・スレイター; ロバート・エンドレ・タルジャン;
ビッグO記法による時間計算量

森林を表現するためのデータ構造

リンク/カットツリーは、フォレスト (ルート付きツリーのセット)を表すデータ構造であり、次の操作を提供します。

単一のノードで構成されるツリーをフォレストに追加します。
いずれかのツリー内のノードが指定されている場合は、そのノード (およびそのサブツリー) を、そのノードが含まれるツリーから切断します。
ノードを別のノードの子として接続します。
与えられたノードから、それが属する木の根を見つけます。この操作を2つの異なるノードに対して行うことで、それらが同じ木に属しているかどうかを確認できます。

表現されたフォレストは非常に深いツリーで構成される場合があり、フォレストを親ポインタツリーの単純なコレクションとして表現すると、特定のノードのルートを見つけるのに長い時間がかかる可能性があります。しかし、フォレスト内の各ツリーをリンク/カットツリーとして表現すると、要素がどのツリーに属するかをO ( log ( n ))の償却時間で見つけることができます。さらに、表現されたフォレストの変更に合わせてリンク/カットツリーのコレクションを迅速に調整できます。特に、マージ（リンク）と分割（カット）をO ( log ( n )) の償却時間で調整できます。

リンク/カットツリーは、表現されたフォレスト内の各ツリーを頂点が互いに素なパスに分割します。各パスは補助データ構造 (多くの場合はスプレイツリーですが、元の論文はスプレイツリーより前に発表されたため、偏りのあるバイナリ検索ツリーが使用されています) によって表現されます。補助データ構造内のノードは、対応する表現されたツリー内の深さによって順序付けられます。1 つのバリエーションであるNaive Partitioningでは、パスはTango Treesと同様に、最近アクセスされたパスとノードによって決定されます。Partitioning by Sizeでは、パスは特定のノードの最も重い子 (最も多くの子を持つ子) によって決定されます。これにより、構造はより複雑になりますが、操作のコストが償却 O(log n) から最悪のケース O(log n) に削減されます。これは、さまざまなネットワークフローの問題を解決したり、データセットをジャイブしたりするために使用されています。

オリジナルの出版物では、SleatorとTarjan はリンク/カットツリーを「動的ツリー」または「動的ダイノツリー」と呼んでいました。

構造

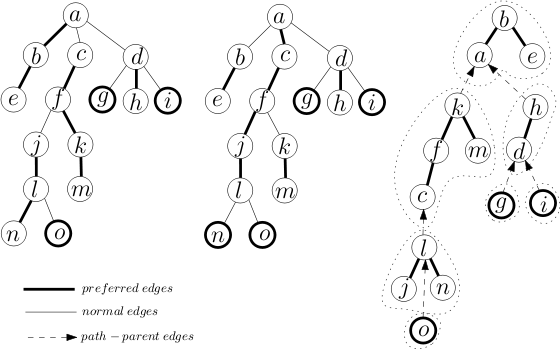
各ノードが任意の数の順序付けられていないノードを持つツリーをパスに分割します。これを表現ツリーと呼びます。これらのパスは内部的に補助ツリー（ここではスプレーツリーを使用します）によって表現されます。補助ツリーでは、左から右へのノードは、ルートからパス上の最後のノードまでのパスを表します。表現ツリー内で接続されているノードのうち、同じ優先パス上にないノード（したがって同じ補助ツリー内にないノード）は、パス親ポインタを介して接続されます。このポインタは、パスを表す補助ツリーのルートに格納されます。

推奨パス

表現された木上でノードvへのアクセスが行われると、そのパスが優先パスとなります。ノードの優先子は、アクセスパス上の最後の子です。最後のアクセスがvであった場合、またはこの木の特定の枝にアクセスが行われなかった場合は null になります。優先エッジは、優先子とvを結ぶエッジです。

別のバージョンでは、優先パスは最も重い子によって決定されます。

オペレーション

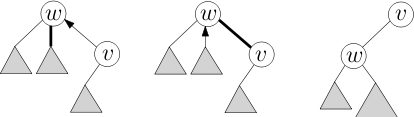
注目する操作はFindRoot(Node v)、、、、です。すべての操作はサブルーチンを使用して実装されます。頂点vCut(Node v)にアクセスすると、表現された木の優先パスは、表現された木のルートRからノードvへのパスに変更されます。アクセスパス上のノードに以前は優先子uがあり、パスが現在子wに向かう場合、古い優先エッジ は削除され（パス親ポインタに変更され）、新しいパスはwを通るようになります。 Link(Node v, Node w)Path(Node v)Access(Node v)

アクセス

ノードvへのアクセスを実行すると、優先される子ノードはなくなり、パスの末尾に配置されます。補助ツリー内のノードは深さによってキー付けされるため、補助ツリー内でvの右側にあるノードはすべて切断される必要があります。スプレーツリーでは、これは比較的単純な手順です。vでスプレーすると、vが補助ツリーのルートになります。次に、vの右側のサブツリー、つまり以前の優先パスでその下にあったすべてのノードを切断します。切断されたツリーのルートには、パスの親ノードへのポインタがあり、これをvにポイントします。

ここで、表現されたツリーをルートRまでたどり、必要に応じて優先パスを切断およびリセットします。これを行うには、vからパスの親ポインタをたどります( vは現在ルートなので、パスの親ポインタに直接アクセスできます)。vがあるパスにすでにルートRが含まれている場合(ノードは深さによってキー付けされているため、補助ツリーの左端のノードになります)、パスの親ポインタは null になり、アクセスは完了です。それ以外の場合は、別のパスwにあるノードへのポインタをたどります。 wの古い優先パスを切断し、 vがあるパスに再接続します。これを行うには、 wで splay し、その右側のサブツリーを切断して、そのパスの親ポインタをwに設定します。すべてのノードは深さによってキー付けされており、 vのパスにあるすべてのノードはwのパスにあるすべてのノードよりも深いため(表現されたツリーではwの子であるため)、 vのツリーをwの右の子として単純に接続します。再びvにスプレーします。vはルートwの子なので、単純にv をルートに回転させます。この処理全体を、 vのパス親ポインタが null になるまで繰り返します。null になった時点で、 v は表現木Rのルートと同じ優先パス上に位置します。

アクセス中に、古い優先パスは破壊され、パス親ポインタに置き換えられ、アクセスされたノードはツリーのルートに広げられる。

ルート検索

FindRoot は、ノードvを含む表現された木のルートを見つけることを意味します。アクセスサブルーチンはv を優先パスに配置するため、まずアクセスを実行します。これでノードvは同じ優先パス上にあり、したがってルートRと同じ補助木になります。補助木は深さによってキー付けされるため、ルートRは補助木の左端のノードになります。そこで、vの左の子を再帰的に選択し、それ以上進めなくなるまで続けます。このノードがルートRです。ルートは線形に深くなる場合があり（これはスプレイ木では最悪のケースです）、そのため、次のアクセスが速くなるようにルートをスプレイします。

カット

ここで、表現されたツリーをノードvで切断します。まず、 vにアクセスします。これにより、表現されたツリー内のvより下位のすべての要素が、補助ツリー内のvの右の子として配置されます。これで、 vの左サブツリーにあるすべての要素は、表現されたツリーでvより上位のノードになります。したがって、 vの左の子(パス親ポインタを通じて元の表現されたツリーへの接続がまだ維持されています) を切断します。これで、v は表現されたツリーのルートになりました。vにアクセスすると、 vの下の優先パスも切断されますが、そのサブツリーは、パス親ポインタを通じて vへの接続を維持します。

リンク

vが木の根であり、wが別の木の頂点である場合、 vとw を含む木に辺(v, w)を追加してリンクし、w をvの親にします。これを行うには、それぞれの木でvとw の両方にアクセスし、 w をvの左の子にします。v は根であり、補助木ではノードは深さによってキー付けされるため、 v にアクセスすると、補助木においてv の左の子は存在しません（根として最小深さであるため）。w を左の子として追加すると、表現された木において wがvの親になります。

パス

この操作では、ルートRからノード v へのパス上のすべてのノード（またはエッジ）に対して、何らかの集計関数（「合計」や「最小」や「最大」や「増加」など）を実行します。これを行うには、 vにアクセスします。これにより、ルートRからノード v へのパス上のすべてのノードを含む補助ツリーが得られます。このデータ構造には、最小値や最大値、サブツリー内のコストの合計など、取得したいデータを追加することができ、これらのデータは、指定されたパスから定数時間で返されます。

演算の擬似コード

スイッチ優先子(x, y):
    if (right(x) が null ではない)
        パス親(右(x)) = x
    右(x) = y
    （yがnullではない）の場合
        親(y) = x

アクセス(v):
    広げる(動詞)
    スイッチ優先子(v, null)
    (path-parent(v)がnullでない場合) 
        w = パスの親(v)
        広げる(w)
        スイッチ優先子(w, v)
        アクセス(v)

リンク(v, w):
    アクセス(v)
    アクセス(w)
    左(v) = w
    親(w) = v

カット(v):
    アクセス(v)
    (left(v)がnullでない場合)
        パスの親(左(v)) = パスの親(v)
        左(v) = null
    パス親(v) = null

分析

カットとリンクのコストはO (1)で、アクセスコストも加算されます。FindRootの上限はO (log n )で、アクセスコストも加算されます。実装によっては、データ構造に追加情報（サブツリー内の最小値または最大値のノードや合計値など）を追加できます。したがって、Pathはこれらの情報にアクセス限界を加えた定数時間で返すことができます。

したがって、実行時間を見つけるには アクセスを制限する必要があります。

Accessはスプレイング（展開）を利用しますが、その償却上限はO (log n )であることが分かっています。したがって、残りの解析では、スプレイングを行う必要のある回数について検討します。これは、木を上に向かって走査する際に、優先される子ノードの変更回数（優先パス内で変更されるエッジの数）に等しくなります。

Heavy-Light Decompositionと呼ばれる手法を使用してアクセスを制限しました。

重軽分解

この手法では、サブツリー内のノード数に応じて、エッジを「重い」または「軽い」と呼びます。⁠ ⁠は、表現されたツリーにおける $Size(v)$ vのサブツリー内のノード数を表します。エッジは、size(v) > 1 ⁄ 2 size(parent(v)) の場合に「重い」と呼ばれます。したがって、各ノードは最大で1つの「重い」エッジを持つことができます。 「重い」エッジではないエッジは「軽い」エッジと呼ばれます。

ライト深度は、ルートから頂点vまでの特定のパス上にあるライトエッジの数を指します。ライト深度≤ lg n は、ライトエッジをトラバースするたびにノード数が少なくとも 2 分の 1 に減少するためです (親のノードの最大半分を持つことができるため)。

したがって、表現されたツリー内の特定のエッジは、heavy-preferred、heavy-unpreferred、light-preferred 、またはlight-unpreferredの 4 つの可能性のいずれかになります。

まず上限を証明します。 $O(\log ^{2}n)$

お（ログ² n）上限

アクセスのスプレイ操作では log nが得られるため、 O (log ²n ) の上限を証明するには、アクセス数を log nに制限する必要があります。

優先辺が変化するたびに、新たな優先辺が形成されます。そこで、形成された優先辺の数を数えます。任意のパスには軽い辺が最大でlog n個存在するため、軽い辺が優先辺に変化する数も最大でlog n個となります。

優先される重いエッジの数は、任意の操作に対して⁠ ⁠できますが、 $O(n)$ ⁠ ⁠ $O(\log n)$ 償却されます。一連の実行を通じて、n -1 個の重いエッジが優先される可能性があります (表現されるツリーには最大でn -1 個の重いエッジがあるため)。ただし、それ以降は、優先される重いエッジの数は、前のステップで非優先になった重いエッジの数と等しくなります。非優先になる重いエッジごとに、軽いエッジが優先される必要があります。優先される可能性のある軽いエッジの数は最大で log nであることは既に説明しました。したがって、 m 個の操作で優先される重いエッジの数は⁠ ⁠ $m(\log n)+(n-1)$ です。十分な操作 ( ⁠ ⁠ ) にわたって、平均すると $m>n-1$ ⁠ ⁠ $O(\log n)$ になります。

改善するお（ログn）上限

優先子ノードの変更回数を⁠ ⁠ $O(\log n)$ に制限したので、優先子ノードの変更回数が償却コスト O(1) であることが示せれば、アクセス操作を⁠ ⁠ $O(\log n)$ に制限できます。これはポテンシャル法を用いて行われます。

補助木におけるvの配下のノード数をs(v)とします。すると、ポテンシャル関数はとなります。拡散の償却コストは次式で制限されることが分かっています。 $\Phi =\sum _{v}\log {s(v)}$

cost(splay(v))\leq 3\left(\log {s(root(v))}-\log {s(v)}\right)+1

拡張後、vはそのパス親ノードwの子であることが分かっています。したがって、次のことがわかります。

s(v)\leq s(w)

この不等式とアクセスの償却コストを使用して、次の式で制限される伸縮合計を算出します。

3\left(\log {s(R)}-\log {s(v)}\right)+O({\text{number of preferred child changes}})

ここで、Rは表現されたツリーのルートであり、優先される子の変更数は⁠ ⁠ $O(\log n)$ . s ( R ) = n であることがわかっているので、⁠ ⁠ $O(\log n)$ は償却されます。

応用

リンク/カット木は、非巡回グラフの動的接続問題を解くために使用できます。2つのノードxとyが与えられたとき、FindRoot(x) = FindRoot(y) の場合にのみ、それらが接続されています。同じ目的で使用できる別のデータ構造として、オイラーツアー木があります。

最大フロー問題を解く場合、リンク/カットツリーを使用すると、Dinic のアルゴリズムの実行時間をからまで改善できます。 $O(V^{2}E)$ $O(VE\log V)$

参照

さらに読む

Sleator, DD; Tarjan, RE (1983). 「動的ツリーのためのデータ構造」. 第13回ACMコンピューティング理論シンポジウム議事録 - STOC '81 (PDF) . pp. 114– 122. doi :10.1145/800076.802464.
Sleator, DD; Tarjan, RE (1985). 「自己調整型二分探索木」(PDF) . Journal of the ACM . 32 (3): 652. doi :10.1145/3828.3835.
Goldberg, AV ; Tarjan, RE (1989). 「負の循環をキャンセルすることによる最小コスト循環の発見」Journal of the ACM . 36 (4): 873. doi :10.1145/76359.76368.– 最小コスト循環への応用
リンクカットツリー: 高度なデータ構造の講義ノート、2012 年春、講義 19。Erik Demaine 教授、Scribes: Justin Holmgren (2012)、Jing Jian (2012)、Maksim Stepanenko (2012)、Mashhood Ishaque (2007)。
https://jeffe.cs.illinois.edu/teaching/datastructures/2006/notes/07-linkcut.pdf