
2次元直交座標系において、横軸をx、縦軸をyとすると、恒等直線[1] [2]または等線[3]はy = xの直線となる。この直線は1:1直線とも呼ばれ、傾きは1である。[4]横軸と縦軸が同じスケールにある場合、恒等直線は横軸に対して45°の角度を形成するため、非公式には45°直線とも呼ばれる。[5]この直線は、理想的な条件下では同一であると予想される2つのデータ セットを比較する2次元散布図の 基準としてよく使用される。2つのデータ セットの対応するデータ ポイントが互いに等しい場合、対応する散布点は正確に恒等直線上に位置する。[6]
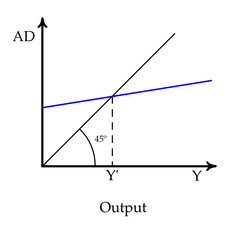
経済学では、ケインズの十字線図において均衡を識別するために恒等線が用いられる。これは、恒等線上でのみ総需要と総供給が等しくなるためである。[7]
参考文献
- ^ Ciesielski, Krzysztof (1997), Set Theory for the Working Mathematician, London Mathematical Society Student Texts, vol. 39, Cambridge University Press, p. 13, ISBN 9780521594653。
- ^ ファインスタイン、アルヴァン・R.(2001)、医療統計の原理、CRCプレス、p.301、ISBN 9781420035681。
- ^ Kotz, Samuel; Read, Campbell B.; Banks, David L. (1997), 統計科学百科事典:最新版、第1巻、Wiley、p. 455、ISBN 9780471118367。
- ^ スターナー、ロバート・ワーナー; エルサー、ジェームズ・J. (2002) 『生態学的化学量論:分子から生物圏までの元素の生物学』プリンストン大学出版局、16ページ、ISBN 9780691074917。
- ^ Challis, N.; Gretton, H. (2008), 基礎工学数学:学生向けワークブック、エルゼビア、p. 38、ISBN 9780857099396。
- ^ van Aartsengel, Aristide; Kurtoglu, Selahattin (2013), Handbook on Continuous Improvement Transformation: The Lean Six Sigma Framework and Systematic Methodology for Implementation, Springer, p. 224, ISBN 9783642359019。
- ^ ミヒル、トーマス・R.(2002)「3.6 ケインズ的交差」マクロ経済理論短期講座、MEシャープ、 35~ 36頁、ISBN 9780765611413。

