脂質二重層の力学

脂質二重膜力学は、脂質二重膜の物理的材料特性を研究する学問であり、二重膜の挙動を生化学的相互作用ではなく、応力とひずみで分類する。膜タンパク質相互作用などの局所点変形は、通常、生物学的液晶の複雑な理論を用いてモデル化されるが、均質な二重膜の機械的特性は、面積膨張係数 K a、曲げ係数 K b、およびエッジエネルギーという 3 つの機械的弾性係数のみで特徴付けられることが多い。流体二重膜の場合、せん断弾性率は定義によりゼロである。これは、平面内で分子が自由に再配置され、その構造がせん断応力に耐えられないことを意味するからである。これらの機械的特性は、膜を介したいくつかの生物学的プロセスに影響を与える。特に、 K aと K bの値は、タンパク質や小分子が二重膜に挿入する能力に影響を与える。 [1] [2]二重膜の機械的特性は、機械的に活性化されたイオンチャネルの機能を変化させることも示されている。[3] Λ {\displaystyle \Lambda }

面積膨張係数

脂質二重層は本質的に二次元構造であるため、K aは通常、平面内でのみ定義されます。直感的には、この係数は、等方性材料の薄板の場合と同様に、二重層の厚さとともに直線的に変化すると予想されるかもしれません。実際にはそうではなく、K aは二重層の厚さにわずかにしか依存しません。この理由は、流体二重層内の脂質は容易に再配置するため、膨張に対する抵抗が分子間結合から生じるバルク材料とは異なり、二重層内の膨張に対する抵抗は、脂質を引き離す際に水にさらされる余分な疎水領域の結果であるためです。 [4]この理解に基づくと、単層の K a の最初の近似値は2γ です。ここで、ガンマは水と脂質の界面の表面張力です。通常、ガンマは 20～50 mJ/m 2の範囲です。[5]二重膜のK a を計算するには、二重膜が2つの単分子膜リーフレットから構成されているため、単分子膜の値に2を掛ける必要があります。この計算に基づくと、脂質二重膜のK aの推定値は80～200 mN/mとなります（注：N/mはJ/m 2に相当します）。関与する力に関するこの理解を踏まえると、研究によりK a が溶液条件によって大きく変化する一方で[6]、尾部の長さと不飽和度によってはほとんど変化しないことが示されていることは驚くべきことではありません。[7]

圧縮弾性率は、二重膜が薄く脆いため、実験的に測定するのが困難であり、その結果、関与する力が小さい。利用されている方法の一つは、浸透圧ストレスに反応して小胞が膨張する様子を調べることである。しかし、この方法は間接的であり、小胞サイズの多分散性によって測定値が変動する可能性がある。[6] Kaを測定するより直接的な方法は、ピペット吸引法であり、単一の巨大単層小胞（GUV）をマイクロピペットで保持して引き伸ばす。[8]最近では、原子間力顕微鏡（AFM）が懸濁した二重膜の機械的特性を調べるために使用されているが、[9]この方法はまだ開発段階にある。

これらの方法すべてに共通する懸念事項は、二重膜が非常に柔軟な構造であるため、サブミクロスケールに至るまで、様々な長さスケールにおいて膜内に大きな熱変動が存在することです。したがって、応力がかかっていない膜に最初に加えられた力は、実際には脂質のパッキングを変化させるのではなく、むしろこれらの起伏を「平滑化」し、結果として機械的特性の誤った値をもたらします。[7]これは大きな誤差の原因となる可能性があります。熱補正を行わない場合のKaの典型的な値は100～150 mN/mですが、熱補正を行うと220～270 mN/mに変化します。

曲げ弾性率

曲げ弾性率は、膜をその自然曲率から別の曲率へ変形させるために必要なエネルギーとして定義されます。理想的な二重膜では固有曲率はゼロであるため、この式は多少簡略化されています。曲げ弾性率、圧縮弾性率、二重膜の厚さは、 これらのパラメータのうち2つが分かればもう1つを計算できるような関係にあります。この関係は、膜を曲げるには内面を圧縮し、外面を伸張させる必要があるという事実に由来します。[4]膜が厚くなるほど、与えられた曲率に対応するために各面が大きく変形する必要があります（曲げモーメントを参照）。文献に記載されているK aの値の多くは、実際には実験的に測定されたK bおよびtの値から計算されています。この関係は小さな変形に対してのみ成立しますが、ほとんどの脂質二重膜は破裂するまでに数パーセントのひずみしか耐えられないため、これは一般的に良い近似値です。[10] K b ＝ K 1つの t 2 {\displaystyle K_{b}=K_{a}t^{2}}

水溶液中のリン脂質によって形成される構造の断面図

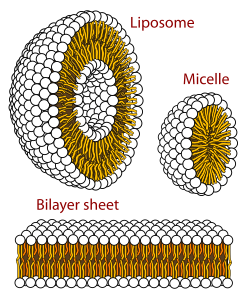
曲率

特定の種類の脂質のみが二重膜を形成できます。脂質が二重膜を形成するかどうかは、主に溶解性と形状という2つの要因によって決まります。二重膜のような自己組織化構造を形成するには、脂質の水への溶解度が低くなければなりません。これは臨界ミセル濃度（CMC）が低いとも言えます。[5] CMCを超えると、分子は凝集し、二重膜、ミセル、逆ミセルなどのより大きな構造を形成します。

特定の脂質がどのような構造を形成するかを決定する主な要因は、その形状（すなわち、固有曲率）である。[4]固有曲率は、ヘッドグループの直径とテールグループの直径の比によって定義される。2つのテールを持つPC脂質の場合、この比はほぼ1であるため、固有曲率はほぼゼロとなる。PSやPEなどの他のヘッドグループはより小さく、結果として得られるジアシル（2つのテールを持つ）脂質は負の固有曲率を持つ。リゾ脂質はテール領域に2つではなく1つのアルキル鎖を持つため、自発曲率が正になる傾向がある。特定の脂質の固有曲率がゼロから大きく逸脱している場合、二重膜を形成しない。[11]

エッジエネルギー

細孔縁における脂質の2つの可能な立体配座を示す模式図。上の画像では脂質は再配列していないため、細孔壁は疎水性である。下の画像では脂質の頭部の一部が折れ曲がっているため、細孔壁は親水性である。

エッジエネルギーは、水に接触する自由端の単位長さあたりのエネルギーです。これは、単位長さ L の二重層に穴を開けるために必要な仕事と考えることができます。このエネルギーの原因は、このような界面を作ると脂質テールの一部が水にさらされることになり、それが不利になるという事実です。また、電気穿孔法や細胞膜の機械的穿孔後の二重層の自己修復特性を制御するため、生物学的現象においても重要なパラメータです。 [8]残念ながら、この特性は実験的に測定することも計算することも困難です。計算における大きな困難の 1 つは、このエッジの構造特性が不明なことです。最も単純なモデルは、テールの全長が露出するように、二重層の向きに変化がないというものです。これは高エネルギーの立体配座であり、このエッジを安定させるために、脂質の一部が頭部基を再配置して、曲がった境界を向くと考えられます。[要出典]これがどの程度起こるかは現在不明ですが、疎水性（尾部がまっすぐ）と親水性（頭部が曲がっている）の両方の孔が共存できるという証拠がいくつかあります。[12] Λ {\displaystyle \Lambda }

有限要素モデリング

FEモデリングは、脂質膜の機械的変形と平衡状態を検証するための強力なツールです。[13]この文脈では、膜は薄殻理論に基づいて扱われ、膜の曲げ挙動は、二重層を非常に薄い物体とみなし、それを2次元表面として解釈するヘルフリッヒ曲げモデルによって記述されます。この考察は、キルヒホッフ-ラブ板理論を脂質二重層に適用して、その応力-変形挙動を決定できることを示唆しています。さらに、FEアプローチでは、二重層表面は個別の要素に分割され、それぞれが上記の2次元力学によって記述されます。[14] [15]

これらの考慮の下では、システム全体の弱形式の仮想仕事は、すべての離散要素の仕事成分の寄与の合計として記述されます。[15]

G ＝ ∑ e ＝ 1 n e l （ G 私 n t e − G e × t e ） {\displaystyle G=\sum _{e=1}^{n_{\mathrm {el} }}\left(G_{\mathrm {int} }^{e}-G_{\mathrm {ext} }^{e}\right)}

各離散要素について、仮想仕事は、加えられた応力と曲げ運動量に対する力ベクトルと変位ベクトルによって決定される。 f {\displaystyle \mathbf {f} } × {\displaystyle \mathbf {x} } σ {\displaystyle \sigma } M {\displaystyle M}

G 私 n t e ＝ δ × e T （ f 私 n t σ e + f 私 n t M e ） {\displaystyle G_{\mathrm {int} }^{e}=\delta \mathbf {x} _{e}^{\mathrm {T} }\left(\mathbf {f} _{\mathrm {int} \sigma }^{e}+\mathbf {f} _{\mathrm {int} M}^{e}\right)}

加えられた二重層応力によるFE力ベクトルは次のように与えられる。 σ α β {\displaystyle \sigma ^{\alpha \beta }}

f 整数  σ e ＝ ∫ σ α β 北 、 α T 1つの β d 1つの {\displaystyle \mathbf {f} _{{\text{int }}\sigma }^{e}=\int \sigma ^{\alpha \beta }\mathbf {N} _{,\alpha }^{\mathrm {T} }{\boldsymbol {a}}_{\beta }\mathrm {d} a}

ここでは点における変位状態関数と 点における二重層表面の接線ベクトルである。 北 α T {\displaystyle \mathbf {N} _{\alpha }^{\mathrm {T} }} α {\displaystyle \alpha} 1つの β {\displaystyle {\boldsymbol {a}}_{\beta }} β {\displaystyle \beta}

上記の内部力と内部仕事の個々の要素ベクトルをグローバル アセンブリで表現すると、次のように離散化された弱形式を取得できます。 f σ e {\displaystyle \mathbf {f} _{\sigma }^{e}} G e {\displaystyle \mathbf {G} ^{e}}

δ × T f （ × 、 q ） + δ q T グラム （ × ） ＝ 0 {\displaystyle \delta \mathbf {x} ^{\mathrm {T} }\mathbf {f} (\mathbf {x} ,\mathbf {q} )+\delta \mathbf {q} ^{\mathrm {T} }\mathbf {g} (\mathbf {x} )=0}

上式において、は各離散要素における変形であり、は面積非圧縮性に関連するラグランジュ乗数である。離散化弱形式は、および のときに満たされる。得られた非線形方程式は、ニュートン法を用いて解く。これにより、脂質膜が様々な刺激に対してとる平衡形状を予測することができる。[14] [16] [17] × {\displaystyle \mathbf {x} } q {\displaystyle \mathbf {q} } f ＝ 0 {\displaystyle \mathbf {f} =0} グラム ＝ 0 {\displaystyle \mathbf {g} =0}

ほとんどの解析は均一な特性（等方性）を持つ脂質膜に対して行われますが、これは単一または少数の脂質種を含む単純な膜にも部分的に当てはまります。しかし、この記述は、細胞膜の場合のように、異なる物質特性を持つ分離した脂質の複数のドメインや膜間タンパク質を含む可能性のある、より複雑な脂質二重層の機械的応答を近似することしかできません。表面流解析、pH、温度依存性を必要とするその他の複雑なケースでは、MDシミュレーションなどの二重層のより離散的なモデルが必要になります。[16] FE法は、次のケースに示すように、外力に対する脂質二重層の平衡構造を予測できます。

テザリング

このシナリオでは、二重層表面の一点が表面に対して垂直な力で引っ張られ、二重層材料の薄いテザーが伸長します。二重層表面の残りの部分は、連続した二重層の引っ張り力を反映した張力Sを受けます。このような場合、引っ張り力の作用する領域の近くにはより細かいメッシュが適用され、二重層の変形をより正確に予測することができます。[16]テザリングは細胞脂質二重層にとって重要な機械的イベントであり、この作用によって膜は基質または細胞骨格の構成要素へのドッキングを媒介することができます。

芽生え

脂質二重層の出芽は生細胞においてよく見られる現象であり、小胞状の代謝産物の輸送に関連しています。この過程において、脂質二重層は内部の静水圧応力と二重層表面に沿ったひずみ制限を受けることで、弾性せん断または粘性せん断によって脂質二重層の一部が伸長することがあります。これは最終的に、典型的な球状の二重層が様々な出芽形状に変形することにつながります。このような形状は、軸に沿って対称であるだけでなく、程度の差はありますが、非対称性も異なります。有限要素解析では、この結果、細長い板状、管状の芽状、対称的な出芽といった出芽平衡形状が示されます。[16]

参考文献

  1. ^ Garcia ML (2004年7月). 「ゲート期待値」. Nature 430 ( 6996): 153–5 . doi :10.1038/430153a. PMID  15241399. S2CID  4427370.
  2. ^ McIntosh TJ, Simon SA (2006). 「膜タンパク質の機能と分布における二重膜材料特性の役割」. Annual Review of Biophysics and Biomolecular Structure . 35 : 177–9 ​​8. doi :10.1146/annurev.biophys.35.040405.102022. PMID  16689633.
  3. ^ Suchyna TM, Tape SE, Koeppe RE, Andersen OS, Sachs F, Gottlieb PA (2004年7月). 「神経活性ペプチドエナンチオマーによる機械感受性チャネルの二重膜依存性阻害」. Nature 430 ( 6996): 235–40 . Bibcode :2004Natur.430..235S. doi :10.1038/nature02743. PMID  15241420. S2CID  4401688.
  4. ^ abc Boal DH (2002).細胞の力学. ケンブリッジ, イギリス: ケンブリッジ大学出版局. ISBN 978-0-521-79681-1。
  5. ^ ab Israelachvili JN (2011).分子間力と表面力（第3版）. バーリントン, マサチューセッツ州: アカデミック・プレス. ISBN 978-0-08-092363-5。
  6. ^ ab Rutkowski CA, Williams LM, Haines TH, Cummins HZ (1991年6月). 「光子相関分光法による合成リン脂質小胞の弾性」.生化学. 30 (23): 5688–96 . doi :10.1021/bi00237a008. PMID  2043611.
  7. ^ ab Rawicz W, Olbrich KC, McIntosh T, Needham D, Evans E (2000年7月). 「脂質二重層の弾性に対する鎖長と不飽和度の作用」. Biophysical Journal . 79 (1): 328–39 . Bibcode :2000BpJ....79..328R. doi :10.1016/S0006-3495(00)76295-3. PMC 1300937. PMID 10866959  . 
  8. ^ ab Evans E, Heinrich V, Ludwig F, Rawicz W (2003年10月). 「動的張力分光法と生体膜の強度」. Biophysical Journal . 85 (4): 2342–50 . Bibcode :2003BpJ....85.2342E. doi :10.1016/S0006-3495(03)74658-X. PMC 1303459. PMID 14507698  . 
  9. ^ Steltenkamp S, Müller MM, Deserno M, Hennesthal C, Steinem C, Janshoff A (2006年7月). 「原子間力顕微鏡法による細孔貫通脂質二重層の機械的特性の解析」. Biophysical Journal . 91 (1): 217–26 . Bibcode :2006BpJ....91..217S. doi :10.1529/biophysj.106.081398. PMC 1479081. PMID 16617084  . 
  10. ^ Hallett FR, Marsh J, Nickel BG, Wood JM (1993年2月). 「小胞の機械的特性. II. 浸透圧膨張および溶解のモデル」. Biophysical Journal . 64 (2): 435–42 . Bibcode :1993BpJ....64..435H. doi :10.1016/S0006-3495(93)81384-5. PMC 1262346. PMID 8457669  . 
  11. ^ Zeidi M, Kim CI (2018年8月). 「膜内粘性が脂質膜の形態に及ぼす影響：完全な解析解」. Scientific Reports . 8 (1) 12845. Bibcode :2018NatSR...812845Z. doi : 10.1038/s41598-018-31251-6 . PMC 6110749. PMID  30150612 . 
  12. ^ Weaver JC, Chizmadzhev YA (1996年12月). 「電気穿孔法の理論：レビュー」.生電気化学と生体エネルギー学. 41 (2): 135– 60. doi :10.1016/S0302-4598(96)05062-3.
  13. ^ Kim J (2020年2月). 「細胞膜のナノメカニカル応答の探究」. Scientific Reports . 10 (1) 2301. Bibcode :2020NatSR..10.2301K. doi :10.1038/s41598-020-59030-2. PMC 7010710. PMID  32041981. 
  14. ^ ab Steigmann DJ (2018).脂質二重膜の研究における力学の役割. Cham. ISBN 978-3-319-56348-0. OCLC  988293321.{{cite book}}: CS1 メンテナンス: 場所の発行元が見つかりません (リンク)
  15. ^ ab Sauer RA (2017-05-25). 「薄殻理論を用いた脂質二重層の計算モデリングについて」.脂質二重層研究における力学の役割. CISM国際機械科学センター. 第577巻. シュプリンガー・インターナショナル・パブリッシング. pp.  221– 286. doi :10.1007/978-3-319-56348-0_5. ISBN 978-3-319-56347-3。
  16. ^ abcd Sauer RA, Duong TX, Mandadapu KK, Steigmann DJ (2017年2月). 「液体シェルの安定化有限要素法と脂質二重層への応用」. Journal of Computational Physics . 330 : 436–466 . arXiv : 1601.03907 . Bibcode :2017JCoPh.330..436S. doi :10.1016/j.jcp.2016.11.004. S2CID  357683.
  17. ^ Bidhendi AJ, Geitmann A (2018年1月). 「植物細胞の形状変化の有限要素モデル化」. Plant Physiology . 176 (1): 41– 56. doi :10.1104/pp.17.01684. PMC 5761827. PMID 29229695  . 
「https://en.wikipedia.org/w/index.php?title=脂質二重層の力学&oldid=1310597123」より取得