最小ボトルネックスパニングツリー

数学において、無向グラフにおける最小ボトルネック全域木（MBST）とは、最もコストのかかる辺が可能な限りコストが低くなる全域木である。ボトルネック辺とは、全域木の中で最も重み付けの高い辺のことである。全域木は、グラフ内にそれより重みの小さいボトルネック辺を持つ全域木が存在しない場合に、最小ボトルネック全域木となる。^[1]有向グラフの場合、同様の問題は最小ボトルネック全域木樹状突起（MBSA）として知られている。

定義

無向グラフ

{\displaystyle G(V,E)} — 最小ボトルネックスパニングツリー⁠ ⁠ $G(V,E)$

無向グラフ $G (V, E)$ と関数 $w : E \to R$ において、 $S を$ すべての全域木T _iの集合とする。B ( T _i )を任意の全域木T _iの最大重み辺とする。最小ボトルネック全域木S ′の部分集合を定義し、任意の $T$ $j$ $\in$ $S$ $'$ と $T$ $k$ $\in$ $S$ に対して、すべてのiと kに対して $B$ $($ $T$ $j$ $) \leq$ $B$ $($ $T$ $k$ $)$ が成り立つものとする。^[2]

右のグラフは MBST の例であり、グラフの赤いエッジは $G (V 、 E)$ の MBST を形成します。

有向グラフ

グラフGの樹状部は、指定されたノードLから $V$ $\{$ $L$ $}$ の部分集合V ′の各ノードへの有向パスを含むGの有向木です。ノードLは樹状部のルートと呼ばれます。樹状部は、 $V$ $' =$ $V$ $\{$ $L$ $}$ のとき全域樹状部です。この場合の MBST は、最小ボトルネックエッジを持つ全域樹状部です。この場合の MBST は、最小ボトルネック全域樹状部 (MBSA) と呼ばれます。

右のグラフは MBSA の例であり、グラフの赤いエッジは $G (V 、 E)$ の MBSA を形成します。

プロパティ

MST（または最小全域木）は必然的にMBSTであるが、MBSTは必ずしもMSTであるわけではない。^[3]

^[4]

無向グラフに対するカメリーニのアルゴリズム

カメリーニは1978年に、与えられた無向・連結・辺重み付きグラフにおいて最小ボトルネック全域木（MBST）を求めるアルゴリズムを提案した^[5]。このアルゴリズムは、辺を2つの集合に分割する。一方の集合の辺の重みは、もう一方の集合の重みと同じである。より小さな辺集合の辺のみで構成される部分グラフに全域木が存在する場合、その部分グラフのMBSTを計算する。部分グラフのMBSTは、元のグラフのMBSTと全く同じである。全域木が存在しない場合は、各切断された構成要素を新しいスーパー頂点に結合し、これらのスーパー頂点とより大きな辺集合の辺で構成されるグラフのMBSTを計算する。各切断された構成要素のフォレストは、元のグラフのMBSTの一部である。この処理を、グラフに2つの（スーパー）頂点が残り、それらの頂点間の重みが最小となる単一の辺が追加されるまで繰り返す。MBSTは、前のステップで見つかったすべての辺から構成される。^[4]

擬似コード

この手順には2つの入力パラメータがある。Gはグラフであり、wはグラフG内のすべての辺の重み配列である。^[6]

関数MBST(グラフG、重みw )
     E ← G 
    の辺の集合| E | = 1の場合、 Eを返すそうでない場合A ← Eの辺の半分で重みが中央値の重み以上であるもの
        B ← E - A F ← G _BのフォレストFが全域木の場合、 MBST( G _B、w )
        を返すそうでない場合、MBST (( G _A ) _η、w ) Fを返す   
        
        
         
            
             $\cup$

上記( G _A ) _ηはスーパー頂点(切断されたコンポーネント内の頂点を1つとみなす)とA内の辺から構成されるサブグラフです。

実行時間

このアルゴリズムはO ( E )時間で実行されます（Eは辺の数）。この限界は次のように達成されます。

中央値探索アルゴリズムを用いて2つの集合に分割する（O（E））
O ( E )で森林を見つける
各反復においてEの半辺を考慮すると、T(E)=T(E/2)+O(E)となる。マスター定理により、全体の時間計算量はO ( E )となる。

注意: 実行時間は O(E+V) ではなく O(E) と推定されます (グラフのトラバースには O(E+V) の時間がかかります)。ただし、この場合、グラフは接続されているため、V-1<=E となり、O(E+V)=O(E) となります。

例

次の例では、緑のエッジを使用して MBST を形成し、破線の赤の領域はアルゴリズムのステップ中に形成されたスーパー頂点を示しています。

	このアルゴリズムは、重みに基づいてエッジを2つの集合に分割します。緑色のエッジは、重みが可能な限り小さいエッジです。
	小さな辺集合の辺のみで形成された部分グラフには全域木が存在するため、この部分グラフでMBSTの探索を繰り返します。
	現在の小さなエッジセットのエッジで形成されたサブグラフには全域木が存在しない。切断されたコンポーネントの頂点をスーパー頂点（赤い破線で示される）に結合し、スーパー頂点と大きなエッジセットのエッジで形成されたサブグラフでMBSTを求める。切断された各コンポーネント内に形成されるフォレストは、元のグラフのMBSTの一部となる。
	さらに多くの頂点をスーパー頂点に結合して、同様の手順を繰り返します。
	アルゴリズムは、アルゴリズムの実行中に見つかったエッジを使用して、最終的に MBST を取得します。

有向グラフのMBSAアルゴリズム

有向グラフには2つのアルゴリズムがあります。MBSAを見つけるためのCameriniのアルゴリズムと、GabowとTarjanによるアルゴリズムです。^[4]

MBSAのためのカメリーニのアルゴリズム

有向グラフの場合、カメリーニのアルゴリズムは、MBSAのボトルネックコストとして最大コストとなる辺の集合を見つけることに焦点を当てています。これは、辺の集合Eを2つの集合AとBに分割し、 G _{T が}全域樹状線を持たないことが分かっている集合Tを維持することで行われます。G ( B ∪ T )の最大樹状線がGの全域樹状線でない場合はTをBだけ増加し、そうでない場合はE をAだけ減少させます。全体の計算時間はO ( E log E ) です。^[5]^[4]

擬似コード

関数MBSA( G , w , T )は
    E ← G 
    の辺の集合であり、 | E − T | > 1であれば
        A ← UH(ET)、
         B ← ( E − T) − A、
        F ← BUSH( G _BUT )
        であり、 FがGの全域樹状であれば
            S ← F
            MBSA(( G _BUT ), w , T )
         else 
            MBSA(G, w , TUB );

TはEの部分集合を表し、G _Tにはノード「a」を根とする全域木が含まれないことが分かっている。初期状態ではTは空である。
UHはGの(E−T)個の辺の集合を取り、次のようなA⊂(E−T)を返す。
1. $|A|=\left\lfloor {\frac {(|ET|)}{2}}\right\rfloor$
2. W _a ≥ W _b（a ∈ A かつ b ∈ B）
BUSH(G)は、ノード「a」を根とするGの最大樹状枝を返す。
最終結果はS

例

	このアルゴリズムの最初の反復を実行すると、 $F$ が得られ、 $F は$ $G$ の全域樹状線ではないので、コードを実行します。 $MBSA(G,w,T\cup B).$
	2回目の反復では、が得られ、これも $G$ の全域樹状線ではないので、コードを実行する。 $F'$ $F'$ $MBSA(G,w,T'\cup B')$
	3回目の反復では、が得られ、これは $G$ の全域樹状線であるので、コードを実行する。 $F''$ $F''$ $MBSA(G_{T''\cup B''},w,T'')$
	を実行すると、は1 に等しくなり、1 より大きくないので、アルゴリズムはを返し、最終結果はになります。 $MBSA(G_{T''\cup B''},w,T'')$ $\|ET\|$ $S=F''$

MBSA の Gabow および Tarjan アルゴリズム

GabowとTarjanは、MBSAを生成する単一ソース最短経路のためのDijkstraアルゴリズムの修正版を提供した。彼らのアルゴリズムは、フィボナッチヒープを用いた場合、 O ( E + V log V )時間で実行される。^[7]

擬似コード

グラフG(V,E) の場合、 FはV内の頂点の集合です。
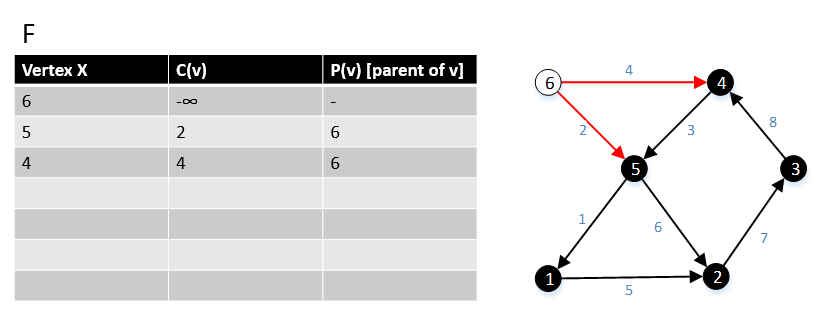
 最初は、F = { s }であり、sはグラフGの開始点であり、c ( s ) = -∞である。

 1  関数MBSA-GT( G , w, T )|V|を
 2      回繰り返す
 3 Fからc ( v )が最小のvを選択します。
 4 Fから削除します。
 5           ∀ edge( v, w )に対して、6 
 w               ∉ Fまたは∉ Treeの場合、 
 7 w をFに追加します。           
 8                   c ( w ) = c ( v,w ) ; 
 9                   p ( w ) = v ;     
 10             そうでなければ11  
 w                  ∈ Fかつc (w) > c(v, w) ならば
 12                      c ( w ) = c ( v, w );
 13                      p ( w ) = v ;

例

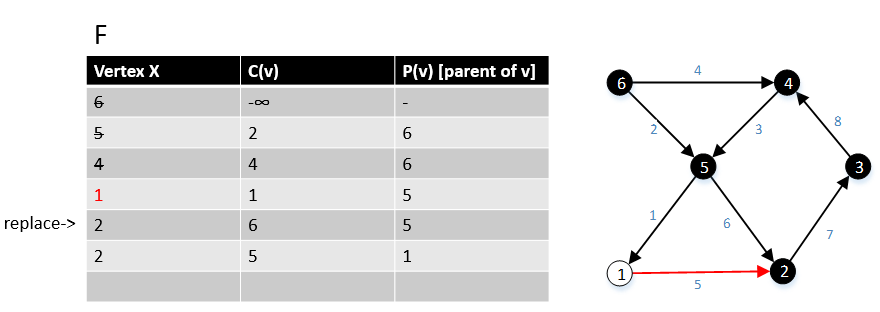
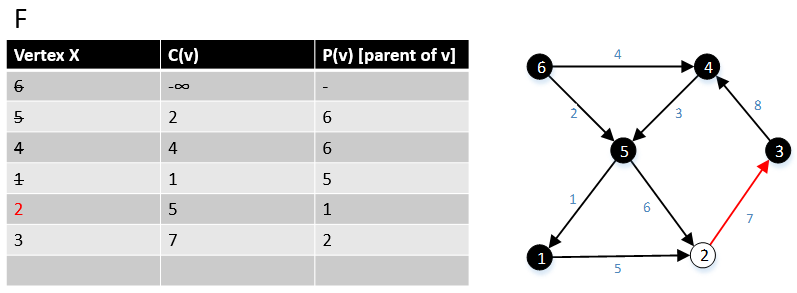
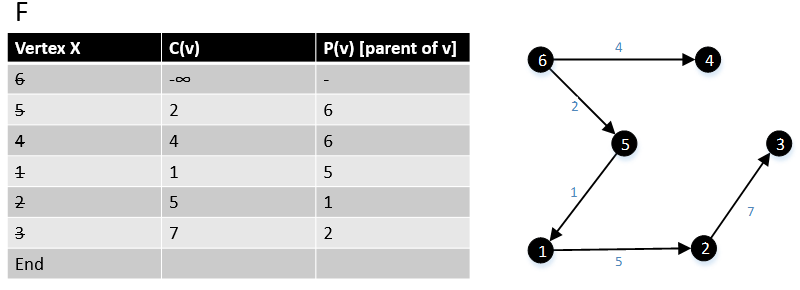
次の例は、アルゴリズムがどのように機能するかを示しています。

アルゴリズムの最初のステップでは、グラフGからルートsを選択します。上図では、頂点6がルートsです。次に、すべての辺(6,w)∈Eとそのコストc(6,w)（w∈V）を求めます。

次にグラフGの頂点5に移動すると、すべてのエッジ(5,w)∈Eとそのコストc(5,w)（w∈V）が見つかります。

次にグラフ G の頂点 4 に移動し、すべてのエッジ (4,w) ∈ E とそのコスト c(4,w) (w ∈ V) を見つけます。エッジ (4,5) > エッジ (6.5) であることがわかったので、エッジ (6,5) を保持し、エッジ (4,5) を削除します。

次にグラフ G の頂点 1 に移動し、すべてのエッジ (1,w) ∈ E とそのコスト c(1,w) (w ∈ V) を見つけます。エッジ (5,2) > エッジ (1,2) であることがわかったので、エッジ (5,2) を削除し、エッジ (1,2) を保持します。

次にグラフGの頂点2に移動すると、すべてのエッジ(2,w)∈Eとそのコストc(2,w)（w∈V）が見つかります。

次にグラフ G の頂点 3 に移動すると、すべてのエッジ (3,w) ∈ E とそのコスト c(3,w) が見つかります (w ∈ V)。エッジ (3,4) > エッジ (6,4) であることがわかったので、エッジ (3,4) を削除してエッジ (6,4) を保持します。

Tarjan と Gabow によって提案された、疎グラフに対する $O (E log * V)$ の境界を持つ別のアプローチは、MBSA に対する Camerini のアルゴリズムと非常によく似ていますが、各反復ごとにエッジのセットを 2 つのセットに分割するのではなく、 $K (i)$ が導入されました。ここで、 iは分割された回数、つまり反復回数であり、 $K (i)$ は反復ごとに持つべき分割されたセットの数を示す増加関数です。 $K (i) = 2 k (i - 1) 、$ $k (1) = 2$ です。アルゴリズムは、任意の MBSA のボトルネックエッジの値である $λ *を見つけます。$ $λ *$ が見つかった後、 $G (λ *)$ 内のすべてのスパニング樹状線は、すべてのエッジのコストが $\leq$ $λ$ $*であるグラフである$ $G (λ *)$ である MBSA です。^[4]^[7]

参考文献

^ ボトルネックスパニングツリーに関するすべて
^ Murali, TM (2009)、最小全域木の応用(PDF)
^ 質問3ではこの主張の証明があります（PDF）
^ abcde Traboulsi, Ahmad (2014), Bottleneck Spanning Trees (PDF) 、 2016年3月4日のオリジナル(PDF)からアーカイブ、2014年12月28日取得
^ ab Camerini, PM (1978)、「最小最大全域木問題といくつかの拡張」、Information Processing Letters、7 (1): 10– 14、doi :10.1016/0020-0190(78)90030-3
^ Cui, Yuxiang (2013), Minimum Bottleneck Spanning Tree (PDF) 、 2016年3月4日時点のオリジナル(PDF)からアーカイブ、2014年12月28日取得
^ ab Gabow, Harold N ; Tarjan, Robert E (1988). 「2つのボトルネック最適化問題に対するアルゴリズム」. Journal of Algorithms . 9 (3): 411– 417. doi :10.1016/0196-6774(88)90031-4. ISSN 0196-6774.

[1] ボトルネックスパニングツリーに関するすべて

[2] Murali, TM (2009)、最小全域木の応用(PDF)

[3] 質問3ではこの主張の証明があります（PDF）

[Traboulsi2014-4] Traboulsi, Ahmad (2014), Bottleneck Spanning Trees (PDF) 、 2016年3月4日のオリジナル(PDF)からアーカイブ、2014年12月28日取得

[Camerini1978-5] Camerini, PM (1978)、「最小最大全域木問題といくつかの拡張」、Information Processing Letters、7 (1): 10– 14、doi :10.1016/0020-0190(78)90030-3

[6] Cui, Yuxiang (2013), Minimum Bottleneck Spanning Tree (PDF) 、 2016年3月4日時点のオリジナル(PDF)からアーカイブ、2014年12月28日取得

[GabowTarjan1988-7] Gabow, Harold N ; Tarjan, Robert E (1988). 「2つのボトルネック最適化問題に対するアルゴリズム」. Journal of Algorithms . 9 (3): 411– 417. doi :10.1016/0196-6774(88)90031-4. ISSN 0196-6774.