直交性

直交性は、文脈に応じてさまざまな意味を持つ用語です。

線分ABと線分CDは互いに垂直です。

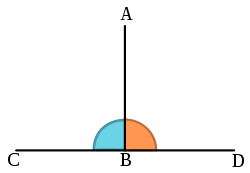
数学において、直交性は幾何学における垂直性の概念を一般化したものである。多くの研究者は「垂直」と「直交」という2つの用語を互換的に使用しているが、 「垂直」という用語は、より具体的には直角を形成するように交差する直線や平面を指すのに対し、「直交」という用語は、直交ベクトルや直交曲線といった一般的な概念を指す。[ 1 ] [ 2 ]

この用語は、物理学、芸術、コンピューターサイエンス、統計学、経済学などの他の分野でも使用されています。

語源

この言葉は、古代ギリシャ語 で「直立」を意味するὀρθός ( orthós ) [ 3 ]と、「角度」を意味するγωνία ( gōnía ) に由来します。[ 4 ]

古代ギリシャ語のὀρθογώνιον（orthogṓnion）と古典ラテン語のorthogoniumは、もともと長方形を意味していました。[ 5 ]後に直角三角形を意味するようになりました。12世紀には、古典期以降のラテン語のorthogonalisが直角、または直角に関連するものを意味するようになりました。[ 6 ]

数学

数学において、直交性は、幾何学的概念の垂直性を双線型形式の線型代数に一般化したものである。

双線型形式を持つベクトル空間の2つの要素uとvは、のとき直交する。双線型形式によっては、ベクトル空間に零ベクトル（非零の自己直交ベクトル）が含まれる場合があり、その場合、直交性は双曲直交性に置き換えられる。 B{\displaystyle B}B（あなた、v）＝0{\displaystyle B(\mathbf {u} ,\mathbf {v} )=0}

関数空間の場合、関数の族は、直交多項式、直交関数、組合せ論などの文脈で、直交基底を形成するために使用されます。

左：円角ϕを介したユークリッド空間と右：双曲角ϕを介したミンコフスキー時空における座標系の直交性と回転の比較（ cとラベル付けされた赤い線は光信号の世界線を示し、ベクトルはこの線上にある場合、それ自身に直交している）。[ 7 ]

物理

光学

光学では、垂直および水平の直線偏光や右回りおよび左回りの円偏光のように、偏光状態が互いに独立して伝播する場合、それらの偏光状態は直交していると言われます。

特殊相対性理論

特殊相対論では、運動の速さによって決定される時間軸は、同じく速さによって決定される同時発生の空間軸と双曲直交する。この理論は同時性の相対性を特徴とする。

双曲直交性

左の図では、回転によってユークリッド直交性が維持されています。右の図では、双曲線 (B) に関する双曲直交性が双曲回転によって維持されています。

幾何学において、共役双曲線の対が与えられたとき、2つの共役直径は双曲的に直交する。この直径の関係はペルガのアポロニウスによって記述され、解析幾何学によって現代化されている。特殊相対論において、双曲的に直交する直線は、同時性の相対性を示す時間的および空間的な方向として現れる。

ミンコフスキー空間のように時間と空間の軸を双曲的に直交させておくと、光の速度を測定するときに一定の結果が得られます。

量子力学

量子力学において、エルミート作用素、、の2つの固有状態が直交するための十分条件（ただし必要条件ではない）は、それらが異なる固有値に対応することである。これは、ディラック記法において、と であれば異なる固有値に対応することを意味する。これは、シュレーディンガー方程式がシュトゥルム・リウヴィル方程式であるという事実（シュレーディンガーの定式化において）、あるいは観測量がエルミート作用素によって与えられるという事実（ハイゼンベルクの定式化において）から導かれる。 ψメートル{\displaystyle \psi_{m}}ψn{\displaystyle \psi_{n}}⟨ψメートル|ψn⟩＝0{\displaystyle \langle \psi _{m}|\psi _{n}\rangle =0}ψメートル{\displaystyle \psi_{m}}ψn{\displaystyle \psi_{n}}

美術

美術において、消失点を指す遠近法上の（仮想的な）線は「直交線」と呼ばれます。「直交線」という用語は、近代美術批評の文献ではしばしば全く異なる意味を持ちます。ピエト・モンドリアンやバーゴイン・ディラーといった画家の作品の多くは、「直交線」を専ら用いていることで知られています。しかし、これは遠近法ではなく、水平または垂直のみの直線で、交差する箇所で直角を形成する線を指しています。例えば、ティッセン＝ボルネミッサ美術館のエッセイには、「モンドリアンは[…]作品全体を直交線と原色のバランスの探求に捧げた」と記されています。[ 8 ]

コンピュータサイエンス

プログラミング言語設計における直交性とは、様々な言語機能を任意の組み合わせで使用して一貫した結果を得ることができる能力である。[ 9 ]この用法は、 Van WijngaardenによってAlgol 68の設計に導入された。

言語の記述、学習、実装を容易にするため、独立した基本概念の数は最小限に抑えられています。一方で、これらの概念は「直交的」に適用され、言語の表現力を最大化しつつ、有害な過剰表現を回避しています。[ 10 ]

直交性とは、システムのコンポーネントによって生成される技術的効果を変更しても、システムの他のコンポーネントに副作用が生じたり伝播したりしないことを保証するシステム設計特性です。これは通常、関心の分離とカプセル化によって実現され、複雑なシステムの実現可能でコンパクトな設計に不可欠です。コンポーネントで構成されるシステムの出現動作は、そのロジックの形式的な定義によって厳密に制御されるべきであり、不十分な統合、つまりモジュールとインターフェースの非直交設計に起因する副作用によって制御されるべきではありません。直交性により、副作用を引き起こさず、副作用に依存しない設計の検証が容易になるため、テストと開発の時間が短縮されます。

直交命令セット

命令セットが直交しているとは、冗長性がなく（つまり、特定のタスクを実行するために使用できる命令が1つしかない）、命令が任意のアドレッシングモードで任意のレジスタを使用できるような設計になっている場合を指します。この用語は、命令を命令フィールドを構成要素とするベクトルと見なすことに由来しています。1つのフィールドは操作対象のレジスタを識別し、もう1つのフィールドはアドレッシングモードを指定します。直交命令セットは、レジスタとアドレッシングモードのすべての組み合わせを一意にエンコードします。[ 12 ]

通信

電気通信において、理想的な受信機が異なる基底関数を用いて、任意の強さの不要な信号を所望の信号から完全に除去できる場合、多重アクセス方式は直交していると言える。そのような方式の一つに時分割多重アクセス（TDMA）があり、直交基底関数は重複しない矩形パルス（「タイムスロット」）である。

直交周波数分割多重

もう一つの方式は直交周波数分割多重化（OFDM）です。これは、単一の送信機が、互いに干渉しないように直交させるために必要な最小周波数間隔で、周波数多重化された一連の信号を使用することを指します。よく知られている例としては、802.11 Wi-Fiの（ a、g、n）バージョン、WiMAX、ITU-T G.hn、北米を除く世界のほとんどの地域で使用されている地上デジタルテレビ放送システムであるDVB-T 、 ADSLの標準形式であるDMT（Discrete Multi Tone）などがあります。

OFDMでは、サブキャリア周波数は互いに直交するように選択されるため、サブチャネル間のクロストークが排除され、キャリア間ガードバンドは不要になります。これにより、送信機と受信機の両方の設計が大幅に簡素化されます。従来のFDMでは、サブチャネルごとに個別のフィルタが必要でした。

統計学、計量経済学、経済学

統計分析を行う際、特定の従属変数に影響を与える独立変数は、相関がない場合には直交していると言われます。[ 13 ]これは共分散が内積を形成するためです。この場合、変数の効果を単回帰で個別にモデル化するか、重回帰を同時にモデル化するかに関係なく、独立変数のいずれかが従属変数に与える影響について同じ結果が得られます。相関が存在する場合、因子は直交しておらず、2 つの方法で異なる結果が得られます。この用法は、期待値(平均) を差し引いて中心化した場合、無相関変数は、観測データ (つまりベクトル) としてもランダム変数 (つまり密度関数) としても、上で説明した幾何学的な意味で直交するという事実から生じます。最大尤度フレームワークに代わる計量経済学の形式論の 1 つである一般化モーメント法は、直交性条件に依存しています。特に、通常最小二乗法の推定量は、説明変数とモデル残差の間の直交性条件から簡単に導くことができます。

分類学

分類学では、直交分類とは、どの項目も複数のグループに属していない分類、つまり、分類が相互に排他的である分類のことです。

化学と生化学

化学および生化学において、直交相互作用とは、2対の物質があり、それぞれの物質がそれぞれの相手と相互作用できるものの、もう一方の物質とは相互作用しないという相互作用です。例えば、DNAには2つの直交対があります。シトシンとグアニンが塩基対を形成し、アデニンとチミンが塩基対を形成しますが、他の塩基対の組み合わせは強く不利です。化学的な例として、テトラジンはトランスシクロオクテンと反応し、アジドはシクロオクチンと交差反応なく反応するため、これらは互いに直交する反応であり、同時に選択的に行うことができます。[ 14 ]

有機合成

有機合成において、直交保護は官能基を互いに独立して 脱保護することを可能にする戦略です。

生体直交化学

バイオ直交化学という用語は、本来の生化学プロセスを妨害することなく生体システム内で起こり得る化学反応を指します。 [ 15 ] [ 16 ] [ 17 ]この用語は、 2003 年にCarolyn R. Bertozziによって造られました。 [ 18 ] [ 19 ]導入されて以来、バイオ直交反応の概念により、グリカン、タンパク質、 [ 20 ]、脂質[ 21 ]などの生体分子を細胞毒性なしに生体システム内でリアルタイムで研究できるようになりました。生体直交性の要件を満たす多くの化学連結戦略が開発されており、その中には、アジドとシクロオクチン間の1,3-双極子環状付加（銅フリークリックケミストリーとも呼ばれる）[ 22 ] 、ニトロンとシクロオクチン間の[ 23 ] 、アルデヒドとケトンからのオキシム/ヒドラゾン形成[ 24 ]、テトラジン連結[ 25 ]、イソシアニドに基づくクリック反応[ 26 ]、そして最近ではクアドリシクラン連結[ 27 ]などがある。

超分子化学

超分子化学において、直交性の概念は、2 つ以上の超分子（多くの場合は非共有結合）相互作用が適合し、他方からの干渉なしに可逆的に形成される可能性を指します。

分析化学

分析化学において、測定または同定を全く異なる方法で行い、それによって測定の信頼性を高める分析は「直交性」と呼ばれます。したがって、直交試験は結果の「クロスチェック」と見なすことができ、「クロス」という概念は直交性の語源と一致しています。直交試験は、新薬申請においてしばしば要求されます。

システムの信頼性

システム信頼性の分野において、直交冗長性とは、バックアップ装置またはバックアップ方法が、エラーが発生しやすい装置またはバックアップ方法とは全く異なる冗長性の形態を指します。直交冗長バックアップ装置またはバックアップ方法の故障モードは、システム全体を壊滅的な故障から保護するために冗長性を必要とする装置またはバックアップ方法の故障モードと交差せず、完全に異なります。

神経科学

神経科学では、刺激のコード化（場所や質など）が重複する脳内の感覚マップを直交マップと呼びます。

哲学

哲学において、二つの主題、著者、あるいは著作が、潜在的に重複あるいは競合する主張を実質的に扱っていない場合、それらは互いに「直交」していると言われる。したがって、哲学の文献は、互いに支持し補完し合う場合もあれば、競合する説明や体系を提示する場合もあり、あるいは、それぞれの著作の範囲、内容、目的が全く無関係な場合にも、互いに直交していると言える。

ゲーム

チェスのような正方形の格子を特徴とするボードゲームでは、「直交」は「同じ行／『ランク』または『列／『ファイル』にある」という意味で用いられます。これは「斜めに隣接する」マス目と対になるものです。[ 28 ]古代中国のボードゲームである囲碁では、プレイヤーは直交するすべての点を占領することで相手の石を奪うことができます。

法

法律では、直交性とは、手続きにおける利益が一致していないが、相互に相関関係や影響を及ぼさず、利益相反が生じないことを指します。

その他の例

ステレオレコードは、左右のステレオチャンネルを1つの溝にエンコードします。レコードのV字型の溝は、互いに90度の角度で壁が傾いており、それぞれの壁の変化が、ステレオ信号を構成する2つのアナログチャンネルのそれぞれを個別にエンコードします。カートリッジは、溝に沿って針が垂直から左右に45度の2つの直交方向に沿って移動する動きを感知します。[ 29 ] 純粋な水平方向の動きはモノラル信号に対応し、両チャンネルが同一（同位相）の信号を伝送するステレオ信号と同等です。

参照

無料辞書のウィクショナリーで「直交」を調べてください。

参考文献

  1. ^ 「垂直」。Merriam -Webster.com辞書。Merriam-Webster。
  2. ^ 「直交」。Merriam -Webster.com辞書。Merriam-Webster。
  3. ^リデルとスコット、「ギリシャ語-英語辞典」s.v. ὀρθός
  4. ^ Liddell と Scott、 A Greek–English Lexicon s.v. γωνία
  5. ^リデルとスコット『ギリシャ語-英語辞典』s.v. ὀρθογώνιον
  6. ^「直交」.オックスフォード英語辞典（第3版）.オックスフォード大学出版局. 2004年9月.
  7. ^ JA Wheeler; C. Misner; KS Thorne (1973). 『重力』 WH Freeman & Co. p. 58. ISBN 0-7167-0344-0。
  8. ^ 「ニューヨーク・シティ 3（未完成）」 。2009年1月31日時点のオリジナルよりアーカイブ。
  9. ^ Michael L. Scott,プログラミング言語語用論、228ページ。
  10. ^ 1968 年、Adriaan van Wijngaarden 他、アルゴリズム言語 ALGOL 68 の改訂レポート、セクション 0.1.2、直交設計
  11. ^ Null, Linda & Lobur, Julia (2006). 『コンピュータの構成とアーキテクチャの基本（第2版）』 Jones & Bartlett Learning. p. 257. ISBN 978-0-7637-3769-6。
  12. ^リンダ・ヌル (2010). 『コンピュータの構成とアーキテクチャの基本』（PDF） . ジョーンズ＆バートレット出版社. pp.  287– 288. ISBN 978-14496000682015年10月10日時点のオリジナルよりアーカイブ（PDF）
  13. ^アタナシオス・パプーリス、S・ウニクリシュナ・ピライ (2002).確率、ランダム変数、確率過程. マグロウヒル. p. 211. ISBN 0-07-366011-6。
  14. ^ Karver, Mark R.; Hilderbrand, Scott A. (2012). 「バイオオルトゴナル反応ペアによる同時選択的マルチターゲットイメージングの実現」. Angewandte Chemie International Edition . 51 (4): 920–2 . Bibcode : 2012ACIE...51..920K . doi : 10.1002/anie.201104389 . PMC 3304098. PMID 22162316 .  
  15. ^ Sletten, Ellen M.; Bertozzi, Carolyn R. (2009). 「バイオオルトゴナルケミストリー：機能性の海で選択性を釣り上げる」 . Angewandte Chemie International Edition . 48 (38): 6974–98 . Bibcode : 2009ACIE...48.6974S . doi : 10.1002 / anie.200900942 . PMC 2864149. PMID 19714693 .  
  16. ^ Prescher, Jennifer A.; Dube, Danielle H.; Bertozzi, Carolyn R. (2004). 「生きた動物における細胞表面の化学的リモデリング」. Nature . 430 (7002): 873–7 . Bibcode : 2004Natur.430..873P . doi : 10.1038 / nature02791 . PMID 15318217. S2CID 4371934 .  
  17. ^ Prescher, Jennifer A; Bertozzi, Carolyn R (2005). 「生体システムにおける化学」. Nature Chemical Biology . 1 (1): 13– 21. doi : 10.1038/nchembio0605-13 . PMID 16407987. S2CID 40548615 .  
  18. ^ Hang, Howard C.; Yu, Chong; Kato, Darryl L.; Bertozzi, Carolyn R. (2003-12-09). 「ムチン型O結合型グリコシル化のプロテオーム解析に向けた代謝標識アプローチ」 . Proceedings of the National Academy of Sciences . 100 (25): 14846– 14851. Bibcode : 2003PNAS..10014846H . doi : 10.1073/pnas.2335201100 . ISSN 0027-8424 . PMC 299823. PMID 14657396 .   
  19. ^ Sletten, Ellen M.; Bertozzi, Carolyn R. (2011). 「メカニズムからマウスへ：2つの生体直交反応の物語」 . Accounts of Chemical Research . 44 (9): 666– 676. doi : 10.1021/ar200148z . PMC 3184615. PMID 21838330 .  
  20. ^ Plass, Tilman; Milles, Sigrid; Koehler, Christine; Schultz, Carsten; Lemke, Edward A. (2011). 「遺伝子コード化銅フリークリックケミストリー」 . Angewandte Chemie International Edition . 50 (17): 3878– 3881. Bibcode : 2011ACIE...50.3878P . doi : 10.1002/anie.201008178 . PMC 3210829. PMID 21433234 .  
  21. ^ Neef, Anne B.; Schultz, Carsten (2009). 「生細胞における脂質の選択的蛍光標識」. Angewandte Chemie International Edition . 48 (8): 1498– 500. Bibcode : 2009ACIE...48.1498N . doi : 10.1002/anie.200805507 . PMID 19145623 . 
  22. ^ Baskin, JM; Prescher, JA; Laughlin, ST; Agard, NJ; Chang, PV; Miller, IA; Lo, A.; Codelli, JA; Bertozzi, CR (2007). 「銅フリークリックケミストリーによるダイナミックin vivoイメージング」 . Proceedings of the National Academy of Sciences . 104 (43): 16793–7 . Bibcode : 2007PNAS..10416793B . doi : 10.1073/pnas.0707090104 . PMC 2040404. PMID 17942682 .  
  23. ^寧、星海;テミング、リンスケ P.ジャン・ドマーホルト。郭潤。ブランコ＝アニア、ダニエル。ディベッツ、マージョーク F.ウォルファート、マーグリート A.恩恵、ヘルト＝ヤン。ヴァン デルフト、フロリス L. (2010)。「ひずみ促進アルキンニトロン付加環化によるタンパク質修飾」。アンゲワンテ・ケミー国際版。49 (17): 3065– 8. Bibcode : 2010ACIE...49.3065N。土井：10.1002/anie.201000408。PMC 2871956。PMID 20333639。  
  24. ^ Yarema, KJ; Mahal, LK; Bruehl, RE; Rodriguez, EC; Bertozzi, CR (1998). 「シアル酸残基へのケトン基の代謝的送達．細胞表面グリコフォーム工学への応用」 . Journal of Biological Chemistry . 273 (47): 31168–79 . doi : 10.1074/jbc.273.47.31168 . PMID 9813021 . 
  25. ^ Blackman, Melissa L.; Royzen, Maksim; Fox, Joseph M. (2008). 「テトラジン連結反応：逆電子要求型ディールス・アルダー反応に基づく高速バイオコンジュゲーション」. Journal of the American Chemical Society . 130 (41): 13518–9 . doi : 10.1021/ja8053805 . PMC 2653060. PMID 18798613 .  
  26. ^ Stöckmann, Henning; Neves, André A.; Stairs, Shaun; Brindle, Kevin M.; Leeper, Finian J. (2011). 「生体分子とのライゲーションにおけるイソニトリルベースのクリックケミストリーの探求」. Organic & Biomolecular Chemistry . 9 (21): 7303–5 . doi : 10.1039/C1OB06424J . PMID 21915395 . 
  27. ^ Sletten, Ellen M.; Bertozzi, Carolyn R. (2011). 「バイオ直交四環式リガシケイン」 . Journal of the American Chemical Society . 133 (44): 17570–3 . Bibcode : 2011JAChS.13317570S . doi : 10.1021 / ja2072934 . PMC 3206493. PMID 21962173 .  
  28. ^ 「chessvariants.org チェス用語集」。
  29. ^図についてはYouTube を参照してください。
「 https://en.wikipedia.org/w/index.php?title=Orthogonality&oldid=1310615715」より取得