板の曲げ

横方向の圧力が作用する、端で固定された円板の曲げ。板の左半分は変形後の形状を示し、右半分は変形前の形状を示しています。この計算はAnsysを使用して実行されました

板の曲げ、または板の曲げとは、外力とモーメントの作用下で、板が板の平面に垂直にたわむことを指します。たわみ量は、適切な板理論の微分方程式を解くことで決定できます。これらのたわみから、板の応力を計算できます。応力が分かれば、破壊理論を用いて、所定の荷重下で板が破損するかどうかを判断できます。

キルヒホッフ・ラブ板の曲げ

平板上の力とモーメント。

定義

厚さ、ヤング率、ポアソン比の薄い長方形板の場合、 板のたわみ、によってパラメータを定義できます${\displaystyle H}$ ${\displaystyle E}$ ${\displaystyle \nu}$ ${\displaystyle w}$

曲げ剛性は次のように表される。

${\displaystyle D={\frac {EH^{3}}{12\left(1-\nu^{2}\right)}}}$

モーメント

単位長さあたりの 曲げモーメントは次のように表されます

${\displaystyle M_{x}=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu {\frac {\partial ^{2}w}{\partial y^{2}}}\right)}$

${\displaystyle M_{y}=-D\left(\nu {\frac {\partial ^{2}w}{\partial x^{2}}}+{\frac {\partial ^{2}w}{\partial y^{2}}}\right)}$

単位長さあたりのねじりモーメントは次のように表さ れる。

${\displaystyle M_{xy}=-D\left(1-\nu \right){\frac {\partial ^{2}w}{\partial x\partial y}}}$

力

単位長さあたりのせん断力は次のように表さ れます

${\displaystyle Q_{x}=-D{\frac {\partial }{\partial x}}\left({\frac {\partial ^{2}w}{\partial x^{2}}}+{\frac {\partial ^{2}w}{\partial y^{2}}}\right)}$

${\displaystyle Q_{y}=-D{\frac {\partial }{\partial y}}\left({\frac {\partial ^{2}w}{\partial x^{2}}}+{\frac {\partial ^{2}w}{\partial y^{2}}}\right)}$

応力

曲げ応力は次のように表されます

${\displaystyle \sigma _{x}=-{\frac {12Dz}{H^{3}}}\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu {\frac {\partial ^{2}w}{\partial y^{2}}}\right)}$

${\displaystyle \sigma _{y}=-{\frac {12Dz}{H^{3}}}\left(\nu {\frac {\partial ^{2}w}{\partial x^{2}}}+{\frac {\partial ^{2}w}{\partial y^{2}}}\right)}$

せん断応力は次のように表されます

${\displaystyle \tau_{xy}=-{\frac{12Dz}{H^{3}}}\left(1-\nu\right){\frac{\partial^{2}w}{\partial x\partial y}}}$

ひずみ

微小変形理論における曲げひずみは次のように 表される

${\displaystyle \epsilon_{x}={\frac {\partial u}{\partial x}}=-z{\frac {\partial ^{2}w}{\partial x^{2}}}}$

${\displaystyle \epsilon _{y}={\frac {\partial v}{\partial y}}=-z{\frac {\partial ^{2}w}{\partial y^{2}}}}$

微小変形理論におけるせん断ひずみは次のように表さ れる。

${\displaystyle \gamma _{xy}={\frac {\partial u}{\partial y}}+{\frac {\partial v}{\partial x}}=-2z{\frac {\partial ^{2}w}{\partial x\partial y}}}$

大変形板理論では、膜ひずみを考慮する。

${\displaystyle \epsilon _{x}={\frac {\partial u}{\partial x}}+{\frac {1}{2}}\left({\frac {\partial w}{\partial x}}\right)^{2}}$

${\displaystyle \epsilon _{y}={\frac {\partial v}{\partial y}}+{\frac {1}{2}}\left({\frac {\partial w}{\partial y}}\right)^{2}}$

${\displaystyle \gamma _{xy}={\frac {\partial u}{\partial y}}+{\frac {\partial v}{\partial x}}+{\frac {\partial w}{\partial x}}{\frac {\partial w}{\partial y}}}$

たわみ

たわみは次のように表されます

${\displaystyle u=-z{\frac {\partial w}{\partial x}}}$

${\displaystyle v=-z{\frac {\partial w}{\partial y}}}$

導出

キルヒホッフ・ラブ板理論における板の支配方程式は^{[1]である。}

${\displaystyle N_{\alpha \beta ,\alpha }=0}$

そして

${\displaystyle M_{\alpha \beta ,\alpha \beta }-q=0}$

展開形では、

${\displaystyle {\cfrac {\partial N_{11}}{\partial x_{1}}}+{\cfrac {\partial N_{21}}{\partial x_{2}}}=0~;~~{\cfrac {\partial N_{12}}{\partial x_{1}}}+{\cfrac {\partial N_{22}}{\partial x_{2}}}=0}$

そして

${\displaystyle {\cfrac {\partial ^{2}M_{11}}{\partial x_{1}^{2}}}+2{\cfrac {\partial ^{2}M_{12}}{\partial x_{1}\partial x_{2}}}+{\cfrac {\partial ^{2}M_{22}}{\partial x_{2}^{2}}}=q}$

は単位面積あたりの横方向の荷重、板の厚さは、応力は、そして ${\displaystyle q(x)}$ ${\displaystyle H=2h}$ ${\displaystyle \sigma _{ij}}$

${\displaystyle N_{\alpha \beta }:=\int _{-h}^{h}\sigma _{\alpha \beta }~dx_{3}~;~~M_{\alpha \beta }:=\int _{-h}^{h}x_{3}~\sigma _{\alpha \beta }~dx_{3}~.}$

この量の単位は、単位長さあたりの力です。この量の単位は、単位長さあたりのモーメントです。 ${\displaystyle N}$ ${\displaystyle M}$

ヤング率とポアソン比を持つ等方性均質板の場合、これらの式は^{[2]のように簡約される。} ${\displaystyle E}$ ${\displaystyle \nu }$

${\displaystyle \nabla ^{2}\nabla ^{2}w=-{\cfrac {q}{D}}~;~~D:={\cfrac {2h^{3}E}{3(1-\nu ^{2})}}={\cfrac {H^{3}E}{12(1-\nu ^{2})}}}$

ここで、プレート中央面のたわみは どこになります。${\displaystyle w(x_{1},x_{2})}$

薄い長方形板の小さなたわみ

これはジェルマン・ラグランジュ板方程式 によって支配される。

${\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}+2{\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}w}{\partial y^{4}}}={\cfrac {q}{D}}}$

この方程式は、理論の基礎を提供したジェルマンの研究を修正する中で、1811 年 12 月にラグランジュによって初めて導き出されました。

薄い長方形板の大きなたわみ

これは、フェップル・フォン・カルマンの プレート方程式によって支配されている。

${\displaystyle {\cfrac {\partial ^{4}F}{\partial x^{4}}}+2{\cfrac {\partial ^{4}F}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}F}{\partial y^{4}}}=E\left[\left({\cfrac {\partial ^{2}w}{\partial x\partial y}}\right)^{2}-{\cfrac {\partial ^{2}w}{\partial x^{2}}}{\cfrac {\partial ^{2}w}{\partial y^{2}}}\right]}$

${\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}+2{\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}w}{\partial y^{4}}}={\cfrac {q}{D}}+{\cfrac {H}{D}}\left({\cfrac {\partial ^{2}F}{\partial y^{2}}}{\cfrac {\partial ^{2}w}{\partial x^{2}}}+{\cfrac {\partial ^{2}F}{\partial x^{2}}}{\cfrac {\partial ^{2}w}{\partial y^{2}}}-2{\cfrac {\partial ^{2}F}{\partial x\partial y}}{\cfrac {\partial ^{2}w}{\partial x\partial y}}\right)}$

応力関数は どこですか。${\displaystyle F}$

円形キルヒホッフ・ラブ板

円板の曲げは、適切な境界条件を課した支配方程式を解くことで調べることができます。これらの解は1829年にポアソンによって初めて発見されました 。このような問題には円筒座標が便利です。これは、円板の中心面からの点の距離です ${\displaystyle z}$

座標フリー形式の支配方程式は

${\displaystyle \nabla ^{2}\nabla ^{2}w=-{\frac {q}{D}}\,.}$

円筒座標では、 ${\displaystyle (r,\theta ,z)}$

${\displaystyle \nabla ^{2}w\equiv {\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial w}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}w}{\partial \theta ^{2}}}+{\frac {\partial ^{2}w}{\partial z^{2}}}\,.}$

対称荷重を受ける円板の場合、、および は、 ${\displaystyle w=w(r)}$

${\displaystyle \nabla ^{2}w\equiv {\frac {1}{r}}{\cfrac {d}{dr}}\left(r{\cfrac {dw}{dr}}\right)\,.}$

したがって、支配方程式は

${\displaystyle {\frac {1}{r}}{\cfrac {d}{dr}}\left[r{\cfrac {d}{dr}}\left\{{\frac {1}{r}}{\cfrac {d}{dr}}\left(r{\cfrac {dw}{dr}}\right)\right\}\right]=-{\frac {q}{D}}\,.}$

とが定数である場合、支配方程式を直接積分すると次の式が得られる。 ${\displaystyle q}$ ${\displaystyle D}$

${\displaystyle w(r)=-{\frac {qr^{4}}{64D}}+C_{1}\ln r+{\cfrac {C_{2}r^{2}}{2}}+{\cfrac {C_{3}r^{2}}{4}}(2\ln r-1)+C_{4}}$

ここで定数である。たわみ面の勾配は ${\displaystyle C_{i}}$

${\displaystyle \phi (r)={\cfrac {dw}{dr}}=-{\frac {qr^{3}}{16D}}+{\frac {C_{1}}{r}}+C_{2}r+C_{3}r\ln r\,.}$

円板の場合、たわみ量とたわみの傾きが において有限であるという条件は、 が成り立つことを意味します。しかし、 が0である必要はありません。なぜなら、 の極限は右から近づくにつれて存在するからです。しかし、 の場合、 の2階微分は中心で発散し、点状の欠陥に対応します。 ${\displaystyle r=0}$ ${\displaystyle C_{1}=0}$ ${\displaystyle C_{3}}$ ${\displaystyle r\ln r\,}$ ${\displaystyle r=0}$ ${\displaystyle C_{3}\neq 0}$ ${\displaystyle w}$

固定端

固定端を持つ円板の場合、板の端（半径 ）にと が成り立ちます。これらの境界条件と を設定すると、次の式が得られます ${\displaystyle w(a)=0}$ ${\displaystyle \phi (a)=0}$ ${\displaystyle a}$ ${\displaystyle C_{3}=0}$

${\displaystyle w(r)=-{\frac {q}{64D}}(a^{2}-r^{2})^{2}\quad {\text{and}}\quad \phi (r)={\frac {qr}{16D}}(a^{2}-r^{2})\,.}$

プレートの面内変位は

${\displaystyle u_{r}(r)=-z\phi (r)\quad {\text{and}}\quad u_{\theta }(r)=0\,.}$

プレートの面内ひずみは

${\displaystyle \varepsilon _{rr}={\cfrac {du_{r}}{dr}}=-{\frac {qz}{16D}}(a^{2}-3r^{2})~,~~\varepsilon _{\theta \theta }={\frac {u_{r}}{r}}=-{\frac {qz}{16D}}(a^{2}-r^{2})~,~~\varepsilon _{r\theta }=0\,.}$

プレートの面内応力は

${\displaystyle \sigma _{rr}={\frac {E}{1-\nu ^{2}}}\left[\varepsilon _{rr}+\nu \varepsilon _{\theta \theta }\right]~;~~\sigma _{\theta \theta }={\frac {E}{1-\nu ^{2}}}\left[\varepsilon _{\theta \theta }+\nu \varepsilon _{rr}\right]~;~~\sigma _{r\theta }=0\,.}$

厚さ の板の場合、曲げ剛性はとなり、 ${\displaystyle 2h}$ ${\displaystyle D=2Eh^{3}/[3(1-\nu ^{2})]}$

${\displaystyle {\begin{aligned}\sigma _{rr}&=-{\frac {3qz}{32h^{3}}}\left[(1+\nu )a^{2}-(3+\nu )r^{2}\right]\\\sigma _{\theta \theta }&=-{\frac {3qz}{32h^{3}}}\left[(1+\nu )a^{2}-(1+3\nu )r^{2}\right]\\\sigma _{r\theta }&=0\,.\end{aligned}}}$

モーメント合力（曲げモーメント）は

${\displaystyle M_{rr}=-{\frac {q}{16}}\left[(1+\nu )a^{2}-(3+\nu )r^{2}\right]~;~~M_{\theta \theta }=-{\frac {q}{16}}\left[(1+\nu )a^{2}-(1+3\nu )r^{2}\right]~;~~M_{r\theta }=0\,.}$

最大半径応力は、次のとおりです。 ${\displaystyle z=h}$ ${\displaystyle r=a}$

${\displaystyle \left.\sigma _{rr}\right|_{z=h,r=a}={\frac {3qa^{2}}{16h^{2}}}={\frac {3qa^{2}}{4H^{2}}}}$

ここで、境界と板の中心における曲げモーメントは ${\displaystyle H:=2h}$

${\displaystyle \left.M_{rr}\right|_{r=a}={\frac {qa^{2}}{8}}~,~~\left.M_{\theta \theta }\right|_{r=a}={\frac {\nu qa^{2}}{8}}~,~~\left.M_{rr}\right|_{r=0}=\left.M_{\theta \theta }\right|_{r=0}=-{\frac {(1+\nu )qa^{2}}{16}}\,.}$

長方形キルヒホッフ・ラブ板

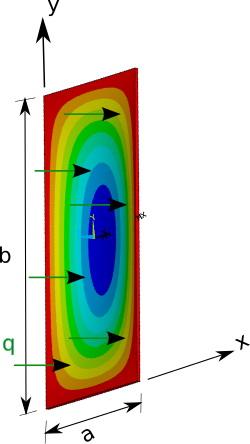
単位面積あたりの分布力の作用下での長方形板の曲げ${\displaystyle q}$

ナビエは1820年に、長方形板を単純支持した場合の変位と応力を求める簡単な方法を発表しました。その考え方は、作用荷重をフーリエ成分で表し、正弦波荷重（単一のフーリエ成分）の解を求め、次にそれらのフーリエ成分を重ね合わせることで任意の荷重の解を得るというものでした。

正弦波負荷

負荷が次の形式であると仮定します

${\displaystyle q(x,y)=q_{0}\sin {\frac {\pi x}{a}}\sin {\frac {\pi y}{b}}\,.}$

ここでは振幅、は -方向のプレート幅、 は -方向のプレート幅です。 ${\displaystyle q_{0}}$ ${\displaystyle a}$ ${\displaystyle x}$ ${\displaystyle b}$ ${\displaystyle y}$

プレートは単純支持されているため、プレートのエッジに沿った変位はゼロ、曲げモーメントはおよびでゼロ、および ではゼロです。 ${\displaystyle w(x,y)}$ ${\displaystyle M_{xx}}$ ${\displaystyle x=0}$ ${\displaystyle x=a}$ ${\displaystyle M_{yy}}$ ${\displaystyle y=0}$ ${\displaystyle y=b}$

これらの境界条件を適用してプレート方程式を解くと、次の解が得られる。

${\displaystyle w(x,y)={\frac {q_{0}}{\pi ^{4}D}}\,\left({\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}\right)^{-2}\,\sin {\frac {\pi x}{a}}\sin {\frac {\pi y}{b}}\,.}$

ここでDは曲げ剛性である

${\displaystyle D={\frac {Et^{3}}{12(1-\nu ^{2})}}}$

曲げ剛性EIに類似しています。^[3]変位がわかれば、プレートの応力とひずみを計算できます。

フォームのより一般的なロードについては

${\displaystyle q(x,y)=q_{0}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}$

ここで、とが整数である場合、解は次のようになる。 ${\displaystyle m}$ ${\displaystyle n}$

${\displaystyle {\text{(1)}}\qquad w(x,y)={\frac {q_{0}}{\pi ^{4}D}}\,\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{-2}\,\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}\,.}$

ナビエ解

二重三角級数方程式

一般的な荷重を次の形で 定義します${\displaystyle q(x,y)}$

${\displaystyle q(x,y)=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }a_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}$

ここで、フーリエ係数は次のように与えられる。 ${\displaystyle a_{mn}}$

${\displaystyle a_{mn}={\frac {4}{ab}}\int _{0}^{b}\int _{0}^{a}q(x,y)\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}\,{\text{d}}x{\text{d}}y}$ 。

小さなたわみに対する古典的な長方形板の方程式は次のようになります。

${\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}+2{\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}w}{\partial y^{4}}}={\cfrac {1}{D}}\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }a_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}$

一般荷重を受ける単純支持板

次のような形の 解を仮定する。${\displaystyle w(x,y)}$

${\displaystyle w(x,y)=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}$

この関数の偏微分は次のように与えられる。

${\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left({\frac {m\pi }{a}}\right)^{4}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}$

${\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left({\frac {m\pi }{a}}\right)^{2}\left({\frac {n\pi }{b}}\right)^{2}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}$

${\displaystyle {\cfrac {\partial ^{4}w}{\partial y^{4}}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left({\frac {n\pi }{b}}\right)^{4}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}$

これらの式をプレート方程式に代入すると、

${\displaystyle \sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left(\left({\frac {m\pi }{a}}\right)^{2}+\left({\frac {n\pi }{b}}\right)^{2}\right)^{2}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\cfrac {a_{mn}}{D}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}$

二つの式を等しくすると、

${\displaystyle \left(\left({\frac {m\pi }{a}}\right)^{2}+\left({\frac {n\pi }{b}}\right)^{2}\right)^{2}w_{mn}={\cfrac {a_{mn}}{D}}}$

これを並べ替えると

${\displaystyle w_{mn}={\frac {1}{\pi ^{4}D}}{\frac {a_{mn}}{\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}}$

単純支持板（コーナー原点）の一般荷重によるたわみは次のように表される。

${\displaystyle w(x,y)={\frac {1}{\pi ^{4}D}}\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {a_{mn}}{\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}$

均一に分布した荷重を受ける単純支持板

長方形板の変位と応力（ mm、mm、mm、GPa、 kPaの荷重下）を示します。赤い線は板の底面、緑の線は中央、青い線は板の上部を表します。${\displaystyle x=a/2}$ ${\displaystyle a=20}$ ${\displaystyle b=40}$ ${\displaystyle H=2h=0.4}$ ${\displaystyle E=70}$ ${\displaystyle \nu =0.35}$ ${\displaystyle q_{0}=-10}$

均一に分布した荷重の場合、

${\displaystyle q(x,y)=q_{0}}$

対応するフーリエ係数は次のように与えられる。

${\displaystyle a_{mn}={\frac {4}{ab}}\int _{0}^{a}\int _{0}^{b}q_{0}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}\,{\text{d}}x{\text{d}}y}$ 。

二重積分を評価すると、

${\displaystyle a_{mn}={\frac {4q_{0}}{\pi ^{2}mn}}(1-\cos m\pi )(1-\cos n\pi )}$ 、

あるいは区分形式では、

${\displaystyle a_{mn}={\begin{cases}{\cfrac {16q_{0}}{\pi ^{2}mn}}&m~{\text{and}}~n~{\text{odd}}\\0&m~{\text{or}}~n~{\text{even}}\end{cases}}}$

均一に分布した荷重を受ける単純支持板（コーナー原点）のたわみは次のように表される。

${\displaystyle w(x,y)={\frac {16q_{0}}{\pi ^{6}D}}\sum _{m=1,3,5,...}^{\infty }\sum _{n=1,3,5,...}^{\infty }{\frac {1}{mn\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}$

板の単位長さあたりの曲げモーメントは次のように表される。

${\displaystyle M_{x}={\frac {16q_{0}}{\pi ^{4}}}\sum _{m=1,3,5,...}^{\infty }\sum _{n=1,3,5,...}^{\infty }{\frac {{\frac {m^{2}}{a^{2}}}+\nu {\frac {n^{2}}{b^{2}}}}{mn\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}$

${\displaystyle M_{y}={\frac {16q_{0}}{\pi ^{4}}}\sum _{m=1,3,5,...}^{\infty }\sum _{n=1,3,5,...}^{\infty }{\frac {{\frac {n^{2}}{b^{2}}}+\nu {\frac {m^{2}}{a^{2}}}}{mn\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}$

レヴィ解

1899年にレヴィ^[4]によって別のアプローチが提案されました。この場合、変位の仮定形から始めて、支配方程式と境界条件が満たされるようにパラメータをフィッティングします。目標は、および における境界条件、そしてもちろん支配方程式を満たすようなものを見つけることです${\displaystyle Y_{m}(y)}$ ${\displaystyle y=0}$ ${\displaystyle y=b}$ ${\displaystyle \nabla ^{2}\nabla ^{2}w=q/D}$

仮に

${\displaystyle w(x,y)=\sum _{m=1}^{\infty }Y_{m}(y)\sin {\frac {m\pi x}{a}}\,.}$

およびに沿って単純支持された板の場合、境界条件はおよびです。これらのエッジに沿った変位に変化がないため および となり、モーメント境界条件はと同等の式 に簡略化されることに注意してください。 ${\displaystyle x=0}$ ${\displaystyle x=a}$ ${\displaystyle w=0}$ ${\displaystyle M_{xx}=0}$ ${\displaystyle \partial w/\partial y=0}$ ${\displaystyle \partial ^{2}w/\partial y^{2}=0}$ ${\displaystyle \partial ^{2}w/\partial x^{2}=0}$

エッジに沿ったモーメント

純モーメント荷重の場合を考えてみましょう。その場合、と は を満たさなければなりません。直交座標系で作業しているので、支配方程式は次のように展開できます ${\displaystyle q=0}$ ${\displaystyle w(x,y)}$ ${\displaystyle \nabla ^{2}\nabla ^{2}w=0}$

${\displaystyle {\frac {\partial ^{4}w}{\partial x^{4}}}+2{\frac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\frac {\partial ^{4}w}{\partial y^{4}}}=0\,.}$

支配方程式に の式を代入すると次のようになる。${\displaystyle w(x,y)}$

${\displaystyle \sum _{m=1}^{\infty }\left[\left({\frac {m\pi }{a}}\right)^{4}Y_{m}\sin {\frac {m\pi x}{a}}-2\left({\frac {m\pi }{a}}\right)^{2}{\cfrac {d^{2}Y_{m}}{dy^{2}}}\sin {\frac {m\pi x}{a}}+{\frac {d^{4}Y_{m}}{dy^{4}}}\sin {\frac {m\pi x}{a}}\right]=0}$

または

${\displaystyle {\frac {d^{4}Y_{m}}{dy^{4}}}-2{\frac {m^{2}\pi ^{2}}{a^{2}}}{\cfrac {d^{2}Y_{m}}{dy^{2}}}+{\frac {m^{4}\pi ^{4}}{a^{4}}}Y_{m}=0\,.}$

これは一般解を持つ 常微分方程式です

${\displaystyle Y_{m}=A_{m}\cosh {\frac {m\pi y}{a}}+B_{m}{\frac {m\pi y}{a}}\cosh {\frac {m\pi y}{a}}+C_{m}\sinh {\frac {m\pi y}{a}}+D_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}}$

ここで、これらは境界条件から決定できる定数である。したがって、変位解は次の式で表される。 ${\displaystyle A_{m},B_{m},C_{m},D_{m}}$

${\displaystyle w(x,y)=\sum _{m=1}^{\infty }\left[\left(A_{m}+B_{m}{\frac {m\pi y}{a}}\right)\cosh {\frac {m\pi y}{a}}+\left(C_{m}+D_{m}{\frac {m\pi y}{a}}\right)\sinh {\frac {m\pi y}{a}}\right]\sin {\frac {m\pi x}{a}}\,.}$

座標系を次のように選び、プレートの境界が（前述と同様に）および（およびではない） であり、境界におけるモーメント境界条件は次のようになる 。${\displaystyle x=0}$ ${\displaystyle x=a}$ ${\displaystyle y=\pm b/2}$ ${\displaystyle y=0}$ ${\displaystyle y=b}$ ${\displaystyle y=\pm b/2}$

${\displaystyle w=0\,,-D{\frac {\partial ^{2}w}{\partial y^{2}}}{\Bigr |}_{y=b/2}=f_{1}(x)\,,-D{\frac {\partial ^{2}w}{\partial y^{2}}}{\Bigr |}_{y=-b/2}=f_{2}(x)}$

ここで、は既知の関数である。これらの境界条件を適用することで解を求めることができる。対称的な場合、 ${\displaystyle f_{1}(x),f_{2}(x)}$

${\displaystyle M_{yy}{\Bigr |}_{y=-b/2}=M_{yy}{\Bigr |}_{y=b/2}}$

そして

${\displaystyle f_{1}(x)=f_{2}(x)=\sum _{m=1}^{\infty }E_{m}\sin {\frac {m\pi x}{a}}}$

我々は

${\displaystyle w(x,y)={\frac {a^{2}}{2\pi ^{2}D}}\sum _{m=1}^{\infty }{\frac {E_{m}}{m^{2}\cosh \alpha _{m}}}\,\sin {\frac {m\pi x}{a}}\,\left(\alpha _{m}\tanh \alpha _{m}\cosh {\frac {m\pi y}{a}}-{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}\right)}$

ここで

${\displaystyle \alpha _{m}={\frac {m\pi b}{2a}}\,.}$

同様に、反対称の場合、

${\displaystyle M_{yy}{\Bigr |}_{y=-b/2}=-M_{yy}{\Bigr |}_{y=b/2}}$

我々は

${\displaystyle w(x,y)={\frac {a^{2}}{2\pi ^{2}D}}\sum _{m=1}^{\infty }{\frac {E_{m}}{m^{2}\sinh \alpha _{m}}}\,\sin {\frac {m\pi x}{a}}\,\left(\alpha _{m}\coth \alpha _{m}\sinh {\frac {m\pi y}{a}}-{\frac {m\pi y}{a}}\cosh {\frac {m\pi y}{a}}\right)\,.}$

対称解と反対称解を重ね合わせると、より一般的な解を得ることができます。

均一に分布した荷重を受ける単純支持板

均一に分布した荷重の場合、

${\displaystyle q(x,y)=q_{0}}$

中心に均一に分布した荷重を受けた 単純支持板のたわみは次のように表される。${\displaystyle \left({\frac {a}{2}},0\right)}$

${\displaystyle {\begin{aligned}&w(x,y)={\frac {q_{0}a^{4}}{D}}\sum _{m=1,3,5,...}^{\infty }\left(A_{m}\cosh {\frac {m\pi y}{a}}+B_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}+G_{m}\right)\sin {\frac {m\pi x}{a}}\\\\&{\begin{aligned}{\text{where}}\quad &A_{m}=-{\frac {2\left(\alpha _{m}\tanh \alpha _{m}+2\right)}{\pi ^{5}m^{5}\cosh \alpha _{m}}}\\&B_{m}={\frac {2}{\pi ^{5}m^{5}\cosh \alpha _{m}}}\\&G_{m}={\frac {4}{\pi ^{5}m^{5}}}\\\\{\text{and}}\quad &\alpha _{m}={\frac {m\pi b}{2a}}\end{aligned}}\end{aligned}}}$

板の単位長さあたりの曲げモーメントは次のように表される。

${\displaystyle M_{x}=-q_{0}\pi ^{2}a^{2}\sum _{m=1,3,5,...}^{\infty }m^{2}\left(\left(\left(\nu -1\right)A_{m}+2\nu B_{m}\right)\cosh {\frac {m\pi y}{a}}+\left(\nu -1\right)B_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}-G_{m}\right)\sin {\frac {m\pi x}{a}}}$

${\displaystyle M_{y}=-q_{0}\pi ^{2}a^{2}\sum _{m=1,3,5,...}^{\infty }m^{2}\left(\left(\left(1-\nu \right)A_{m}+2B_{m}\right)\cosh {\frac {m\pi y}{a}}+\left(1-\nu \right)B_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}-\nu G_{m}\right)\sin {\frac {m\pi x}{a}}}$

均一かつ対称的なモーメント荷重

荷重が対称でモーメントが均一である特殊なケースでは、 ${\displaystyle y=\pm b/2}$

${\displaystyle M_{yy}=f_{1}(x)={\frac {4M_{0}}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{2m-1}}\,\sin {\frac {(2m-1)\pi x}{a}}\,.}$

長方形板の端と端に沿って均一な曲げモーメントを受ける場合の変位と応力。曲げ応力は板の底面に沿って作用する。横せん断応力は板の中央面に沿って作用する。${\displaystyle y=-b/2}$ ${\displaystyle y=b/2}$ ${\displaystyle \sigma _{yy}}$ ${\displaystyle \sigma _{yz}}$

結果として生じる変位は

${\displaystyle {\begin{aligned}&w(x,y)={\frac {2M_{0}a^{2}}{\pi ^{3}D}}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)^{3}\cosh \alpha _{m}}}\sin {\frac {(2m-1)\pi x}{a}}\times \\&~~\left[\alpha _{m}\,\tanh \alpha _{m}\cosh {\frac {(2m-1)\pi y}{a}}-{\frac {(2m-1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}\right]\end{aligned}}}$

ここで

${\displaystyle \alpha _{m}={\frac {\pi (2m-1)b}{2a}}\,.}$

変位に対応する曲げモーメントとせん断力は ${\displaystyle w}$

${\displaystyle {\begin{aligned}M_{xx}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu \,{\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&={\frac {2M_{0}(1-\nu )}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\times \\&~\sin {\frac {(2m-1)\pi x}{a}}\,\times \\&~\left[-{\frac {(2m-1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}+\right.\\&\qquad \qquad \qquad \qquad \left.\left\{{\frac {2\nu }{1-\nu }}+\alpha _{m}\tanh \alpha _{m}\right\}\cosh {\frac {(2m-1)\pi y}{a}}\right]\\M_{xy}&=(1-\nu )D{\frac {\partial ^{2}w}{\partial x\partial y}}\\&=-{\frac {2M_{0}(1-\nu )}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\times \\&~\cos {\frac {(2m-1)\pi x}{a}}\,\times \\&~\left[{\frac {(2m-1)\pi y}{a}}\cosh {\frac {(2m-1)\pi y}{a}}+\right.\\&\qquad \qquad \qquad \qquad \left.(1-\alpha _{m}\tanh \alpha _{m})\sinh {\frac {(2m-1)\pi y}{a}}\right]\\Q_{zx}&={\frac {\partial M_{xx}}{\partial x}}-{\frac {\partial M_{xy}}{\partial y}}\\&={\frac {4M_{0}}{a}}\sum _{m=1}^{\infty }{\frac {1}{\cosh \alpha _{m}}}\,\times \\&~\cos {\frac {(2m-1)\pi x}{a}}\cosh {\frac {(2m-1)\pi y}{a}}\,.\end{aligned}}}$

応力は

${\displaystyle \sigma _{xx}={\frac {12z}{h^{3}}}\,M_{xx}\quad {\text{and}}\quad \sigma _{zx}={\frac {1}{\kappa h}}\,Q_{zx}\left(1-{\frac {4z^{2}}{h^{2}}}\right)\,.}$

円筒板の曲げ

円筒曲げは、寸法がで厚さが小さい長方形板が、板の平面に垂直な均一分布荷重を受けるときに発生します。このような板は円筒面の形状をとります ${\displaystyle a\times b\times h}$ ${\displaystyle a\ll b}$ ${\displaystyle h}$

軸方向に固定された端部を持つ単純支持プレート

回転は自由だが、固定されたエッジを持つ円筒曲げを受ける単純支持板の場合、ナビエ法とレヴィ法を用いて円筒曲げの解を求めることができます。 ${\displaystyle x_{1}}$

厚いミンドリン板の曲げ

厚板の場合、変形後の板厚方向のせん断が中立面法線の向きに及ぼす影響を考慮する必要があります。 レイモンド・D・ミンドリンの理論は、このような板の変形と応力を求める一つのアプローチを提供します。ミンドリンの理論の解は、正準関係を用いて等価なキルヒホッフ・ラブ解から導くことができます。^[5]

支配方程式

^{等方性厚板の標準的な支配方程式は[5]}のように表される

${\displaystyle {\begin{aligned}&\nabla ^{2}\left({\mathcal {M}}-{\frac {\mathcal {B}}{1+\nu }}\,q\right)=-q\\&\kappa Gh\left(\nabla ^{2}w+{\frac {\mathcal {M}}{D}}\right)=-\left(1-{\cfrac {{\mathcal {B}}c^{2}}{1+\nu }}\right)q\\&\nabla ^{2}\left({\frac {\partial \varphi _{1}}{\partial x_{2}}}-{\frac {\partial \varphi _{2}}{\partial x_{1}}}\right)=c^{2}\left({\frac {\partial \varphi _{1}}{\partial x_{2}}}-{\frac {\partial \varphi _{2}}{\partial x_{1}}}\right)\end{aligned}}}$

ここで、は横方向荷重、はせん断弾性率、 は曲げ剛性、は板厚、 はせん断補正係数、はヤング率、はポアソン比、 ${\displaystyle q}$ ${\displaystyle G}$ ${\displaystyle D=Eh^{3}/[12(1-\nu ^{2})]}$ ${\displaystyle h}$ ${\displaystyle c^{2}=2\kappa Gh/[D(1-\nu )]}$ ${\displaystyle \kappa }$ ${\displaystyle E}$ ${\displaystyle \nu }$

${\displaystyle {\mathcal {M}}=D\left[{\mathcal {A}}\left({\frac {\partial \varphi _{1}}{\partial x_{1}}}+{\frac {\partial \varphi _{2}}{\partial x_{2}}}\right)-(1-{\mathcal {A}})\nabla ^{2}w\right]+{\frac {2q}{1-\nu ^{2}}}{\mathcal {B}}\,.}$

ミンドリンの理論では、はプレートの中央面の横方向変位であり、および はそれぞれおよび 軸を中心とした中央面法線の回転です。この理論の標準パラメータはおよびです。せん断補正係数は通常 という値を持ちます。 ${\displaystyle w}$ ${\displaystyle \varphi _{1}}$ ${\displaystyle \varphi _{2}}$ ${\displaystyle x_{2}}$ ${\displaystyle x_{1}}$ ${\displaystyle {\mathcal {A}}=1}$ ${\displaystyle {\mathcal {B}}=0}$ ${\displaystyle \kappa }$ ${\displaystyle 5/6}$

支配方程式の解は、対応するキルヒホッフ・ラブ解が分かっていれば、次の関係式を使って求めることができる。

${\displaystyle {\begin{aligned}w&=w^{K}+{\frac {{\mathcal {M}}^{K}}{\kappa Gh}}\left(1-{\frac {{\mathcal {B}}c^{2}}{2}}\right)-\Phi +\Psi \\\varphi _{1}&=-{\frac {\partial w^{K}}{\partial x_{1}}}-{\frac {1}{\kappa Gh}}\left(1-{\frac {1}{\mathcal {A}}}-{\frac {{\mathcal {B}}c^{2}}{2}}\right)Q_{1}^{K}+{\frac {\partial }{\partial x_{1}}}\left({\frac {D}{\kappa Gh{\mathcal {A}}}}\nabla ^{2}\Phi +\Phi -\Psi \right)+{\frac {1}{c^{2}}}{\frac {\partial \Omega }{\partial x_{2}}}\\\varphi _{2}&=-{\frac {\partial w^{K}}{\partial x_{2}}}-{\frac {1}{\kappa Gh}}\left(1-{\frac {1}{\mathcal {A}}}-{\frac {{\mathcal {B}}c^{2}}{2}}\right)Q_{2}^{K}+{\frac {\partial }{\partial x_{2}}}\left({\frac {D}{\kappa Gh{\mathcal {A}}}}\nabla ^{2}\Phi +\Phi -\Psi \right)+{\frac {1}{c^{2}}}{\frac {\partial \Omega }{\partial x_{1}}}\end{aligned}}}$

ここで、 はキルヒホッフ・ラブ板の予測変位、は となるような重調和関数、はラプラス方程式を満たす関数、であり、 ${\displaystyle w^{K}}$ ${\displaystyle \Phi }$ ${\displaystyle \nabla ^{2}\nabla ^{2}\Phi =0}$ ${\displaystyle \Psi }$ ${\displaystyle \nabla ^{2}\Psi =0}$

${\displaystyle {\begin{aligned}{\mathcal {M}}&={\mathcal {M}}^{K}+{\frac {\mathcal {B}}{1+\nu }}\,q+D\nabla ^{2}\Phi ~;~~{\mathcal {M}}^{K}:=-D\nabla ^{2}w^{K}\\Q_{1}^{K}&=-D{\frac {\partial }{\partial x_{1}}}\left(\nabla ^{2}w^{K}\right)~,~~Q_{2}^{K}=-D{\frac {\partial }{\partial x_{2}}}\left(\nabla ^{2}w^{K}\right)\\\Omega &={\frac {\partial \varphi _{1}}{\partial x_{2}}}-{\frac {\partial \varphi _{2}}{\partial x_{1}}}~,~~\nabla ^{2}\Omega =c^{2}\Omega \,.\end{aligned}}}$

単純支持長方形板

単純に支持された板の場合、マーカスモーメントの合計はゼロになる。すなわち、

${\displaystyle {\mathcal {M}}={\frac {1}{1+\nu }}(M_{11}+M_{22})=D\left({\frac {\partial \varphi _{1}}{\partial x_{1}}}+{\frac {\partial \varphi _{2}}{\partial x_{2}}}\right)=0\,.}$

これはw[ref 6]のラプラス方程式とほぼ等しい。その場合、関数、 、は消え、ミンドリン解は対応するキルヒホッフ解と次のように関係する。 ${\displaystyle \Phi }$ ${\displaystyle \Psi }$ ${\displaystyle \Omega }$

${\displaystyle w=w^{K}+{\frac {{\mathcal {M}}^{K}}{\kappa Gh}}\,.}$

ライスナー・シュタイン片持ち板の曲げ

片持ち板のライスナー・スタイン理論^[6]は、集中端荷重を受ける片持ち板に対して次のような連立常微分方程式を導く。 ${\displaystyle q_{x}(y)}$ ${\displaystyle x=a}$

${\displaystyle {\begin{aligned}&bD{\frac {\mathrm {d} ^{4}w_{x}}{\mathrm {d} x^{4}}}=0\\&{\frac {b^{3}D}{12}}\,{\frac {\mathrm {d} ^{4}\theta _{x}}{\mathrm {d} x^{4}}}-2bD(1-\nu ){\cfrac {d^{2}\theta _{x}}{dx^{2}}}=0\end{aligned}}}$

そして境界条件は ${\displaystyle x=a}$

${\displaystyle {\begin{aligned}&bD{\cfrac {d^{3}w_{x}}{dx^{3}}}+q_{x1}=0\quad ,\quad {\frac {b^{3}D}{12}}{\cfrac {d^{3}\theta _{x}}{dx^{3}}}-2bD(1-\nu ){\cfrac {d\theta _{x}}{dx}}+q_{x2}=0\\&bD{\cfrac {d^{2}w_{x}}{dx^{2}}}=0\quad ,\quad {\frac {b^{3}D}{12}}{\cfrac {d^{2}\theta _{x}}{dx^{2}}}=0\,.\end{aligned}}}$

この2つの常微分方程式の解は次のように表される。

${\displaystyle {\begin{aligned}w_{x}(x)&={\frac {q_{x1}}{6bD}}\,(3ax^{2}-x^{3})\\\theta _{x}(x)&={\frac {q_{x2}}{2bD(1-\nu )}}\left[x-{\frac {1}{\nu _{b}}}\,\left({\frac {\sinh(\nu _{b}a)}{\cosh[\nu _{b}(x-a)]}}+\tanh[\nu _{b}(x-a)]\right)\right]\end{aligned}}}$

ここで、変位に対応する曲げモーメントとせん断力は 、 ${\displaystyle \nu _{b}={\sqrt {24(1-\nu )}}/b}$ ${\displaystyle w=w_{x}+y\theta _{x}}$

${\displaystyle {\begin{aligned}M_{xx}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu \,{\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&=q_{x1}\left({\frac {x-a}{b}}\right)-\left[{\frac {3yq_{x2}}{b^{3}\nu _{b}\cosh ^{3}[\nu _{b}(x-a)]}}\right]\times \\&\quad \left[6\sinh(\nu _{b}a)-\sinh[\nu _{b}(2x-a)]+\sinh[\nu _{b}(2x-3a)]+8\sinh[\nu _{b}(x-a)]\right]\\M_{xy}&=(1-\nu )D{\frac {\partial ^{2}w}{\partial x\partial y}}\\&={\frac {q_{x2}}{2b}}\left[1-{\frac {2+\cosh[\nu _{b}(x-2a)]-\cosh[\nu _{b}x]}{2\cosh ^{2}[\nu _{b}(x-a)]}}\right]\\Q_{zx}&={\frac {\partial M_{xx}}{\partial x}}-{\frac {\partial M_{xy}}{\partial y}}\\&={\frac {q_{x1}}{b}}-\left({\frac {3yq_{x2}}{2b^{3}\cosh ^{4}[\nu _{b}(x-a)]}}\right)\times \left[32+\cosh[\nu _{b}(3x-2a)]-\cosh[\nu _{b}(3x-4a)]\right.\\&\qquad \left.-16\cosh[2\nu _{b}(x-a)]+23\cosh[\nu _{b}(x-2a)]-23\cosh(\nu _{b}x)\right]\,.\end{aligned}}}$

応力は

${\displaystyle \sigma _{xx}={\frac {12z}{h^{3}}}\,M_{xx}\quad {\text{and}}\quad \sigma _{zx}={\frac {1}{\kappa h}}\,Q_{zx}\left(1-{\frac {4z^{2}}{h^{2}}}\right)\,.}$

端部に作用する荷重が一定の場合、端部集中荷重を受ける梁の解が得られます。作用する荷重がの線形関数である場合、 ${\displaystyle y}$

${\displaystyle q_{x1}=\int _{-b/2}^{b/2}q_{0}\left({\frac {1}{2}}-{\frac {y}{b}}\right)\,{\text{d}}y={\frac {bq_{0}}{2}}~;~~q_{x2}=\int _{-b/2}^{b/2}yq_{0}\left({\frac {1}{2}}-{\frac {y}{b}}\right)\,{\text{d}}y=-{\frac {b^{2}q_{0}}{12}}\,.}$

参照

• 曲げ
• 微小ひずみ理論
• キルヒホッフ・ラブ板理論
• 線形弾性
• ミンドリン・ライスナー板理論
• 板理論
• 応力（力学）
• 応力合力
• 構造音響
• 板の振動

参考文献

1. Reddy, JN, 2007,弾性板とシェルの理論と解析, CRC Press, Taylor and Francis
2. Timoshenko, S. および Woinowsky-Krieger, S.、(1959)、「プレートとシェルの理論」、McGraw-Hill New York。
3. Cook, RD et al., 2002,有限要素解析の概念と応用, John Wiley & Sons
4. Lévy, M.、1899 年、Comptes rendues、vol. 129、535-539ページ
5. Lim, GTおよびReddy, JN、2003、「プレートに対する標準的な曲げ関係について」、International Journal of Solids and Structures、vol. 40、pp. 3039-3067。
6. E. ReissnerとM. Stein「片持ち梁板のねじりと横方向曲げ」技術ノート2369、全米航空諮問委員会、ワシントン、1951年。