化学および結晶学において、対称要素とは、対称操作を行うことができる点、直線、または平面のことである。特に、対称要素は鏡面、回転軸(固有回転軸および非固有回転軸)、または反転中心となり得る。[1] [2] [3]分子や結晶 などの物体の場合、対称要素は対称操作の集合に対応する。対称操作とは、対称要素を用いて物体を変化させない剛体変換である。これらの操作を含む集合は、物体の対称群の1つを形成する。この対称群の要素を「対称要素」自体と混同してはならない。大まかに言えば、対称要素とは、対称操作における固定点の幾何学的集合である。例えば、軸を中心とした回転の場合、軸上の点は移動せず、鏡映の場合、変化しない点が対称面を構成する。
恒等元
恒等対称元はすべての物体に存在し、Eと表記されます。[4]これは物体に何もしない操作に対応します。すべての分子は、何もしなければそれ自体と区別がつかないため、すべての物体は少なくとも恒等元を持っています。E以外の対称元を持たない物体は非対称と呼ばれます。そのような物体は必然的にキラルです。[5]

臭化クロロフルオロヨードメタン分子は非対称です。つまり、同一性以外に対称性はありません。
鏡面
鏡面はσで表されます。対称軸を持つ分子では、対称軸を含む鏡面は垂直鏡面と呼ばれ、σ vと表記されます。対称軸に垂直な鏡面は水平鏡面と呼ばれ、 σ hと表記されます。2つのC2軸間の角度を二等分する垂直鏡面は二面角鏡面と呼ばれ、σ dと表記されます。[6]

回転対称性
回転対称性(放射対称性とも呼ばれる)は、対応する対称操作において物体が回転する軸によって表される。真回転群はC nと表記され、物体を復元する回転角度は360/n(C 2 = 180度回転、C 3 = 120度回転、C 4 = 90度回転、C 5 = 72度回転)である。[4] C n表記は、より抽象的な関連群である巡回群にも用いられる。
不適切回転は、軸の周りの回転と、その軸に垂直な平面での鏡映を組み合わせたものである。[2]回転と鏡映の順序は重要ではない(つまり、これらの操作は可換である)。不適切回転は、軸の周りの回転と、軸上の点の周りの反転を組み合わせたものとしても定義される。[3]これらの定義は、点の周りの反転が任意の軸の周りの 180° 回転と、その軸に垂直な平面の周りの鏡映と同等であるため、同等である。不適切回転の対称要素は、回転軸と、鏡面、反転点、またはその両方である。位数 2 nの不適切回転群はS 2 nと表記される。
反転
反転( iと表記)では、物体の中心に反転中心となる点がなければなりません。反転とは、各点を反転中心を通り、分子の反対側の同じ距離まで移動させることです。3次元座標の反転操作では、反転中心は原点 (0,0,0) です。物体が反転されると、物体内の点の位置ベクトル ⟨x,y,z⟩ は ⟨-x,-y,-z⟩ に反転されます
ギャラリー
-
垂直鏡面の例。
-
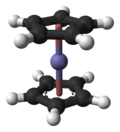
フェロセン分子はS 10対称性を持つ物体です。その対称要素は、垂直な回転軸、水平面、そして中心の反転点です。
参照
参考文献
- ^ Robert G. Mortimer (2005年6月10日). Mathematics for Physical Chemistry. Academic Press. pp. 276–. ISBN 978-0-08-049288-9。
- ^ ab 「対称要素」。オンライン結晶学辞典。2021年9月25日。2021年9月25日閲覧
- ^ ab Wolff, PM de; et al. (1989). 「空間群および点群における対称要素の定義.対称性の命名法に関する国際結晶学連合特別委員会報告書」. Acta Crystallographica Section A. 45 ( 7): 494– 499. doi : 10.1107/S0108767389002230 . ISSN 0108-7673 . 2021年9月29日閲覧。
- ^ ab バーンズ、ジェラルド、グレイザー、AM (2013).固体科学者のための空間群. エルゼビア. doi :10.1016/c2011-0-05712-5. ISBN 978-0-12-394400-9。
- ^ アトキンス、ピーター (2006).アトキンスの物理化学. イギリスのオックスフォード大学出版局(WHフリーマン・アンド・カンパニー)より出版。p. 405. ISBN 0-7167-8759-8。
- ^ スマート、レスリー(2005年)『固体化学:入門』エレイン・ムーア(第3版)ボカラトン:CRCプレス。ISBN 0-7487-7516-1 OCLC 56661923