スペクトラム（物理科学）
電磁スペクトルを示す図

物理科学において、スペクトルとは周波数または波長値の連続的な範囲を指します。この用語は当初、白色光がプリズムを通して分散された際に観測される色の範囲を指し、 17世紀にアイザック・ニュートンによって光学に導入されました。 [ 1 ] [ 2 ]

この概念は後に、音波や海の波など、さまざまな周波数と波長を示す他の波（ノイズスペクトル、海の波スペクトルなど）にも拡張されました。フーリエ解析から始まったスペクトルの概念は信号理論へと拡張され、信号を周波数の関数としてグラフ化し、選択した周波数範囲に情報を配置できるようになりました。現在では、連続する独立変数に直接依存し、その範囲に沿って測定可能な任意の量を、その範囲またはスペクトルに沿ってグラフ化できます。例としては、電子分光法における電子エネルギーの範囲や、質量分析法における質量電荷比の範囲が挙げられます。

語源

ラテン語でスペクトルは「像」または「幻影」を意味し、「亡霊」の意味も含んでいます。スペクトル証拠とは、物理的に存在しない人物の幽霊によって行われたことに関する証言、あるいはサタンの幽霊や幻影が言ったことに関する伝聞証拠です。17世紀後半、マサチューセッツ州セーラムで多くの魔女が有罪判決を受ける際に用いられました。「スペクトル」[Spektrum]という言葉は、ゲーテの『色彩論』やショーペンハウアーの『視覚と色彩について』において、幽霊のような光学的残像を指すために厳密に用いられました。

接頭辞「spectro-」は、スペクトルに関連する単語を形成する際に使用されます。例えば、分光計はスペクトルを記録するための装置であり、分光法は分光計を用いて化学分析を行うことを指します。

電磁スペクトル

蛍光灯の電磁放射スペクトル

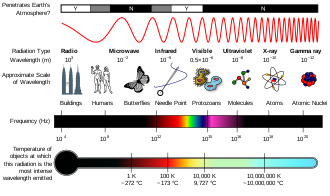
電磁スペクトルは、電磁放射の全周波数範囲を指します[ 3 ]また、特定の物体によって放出または吸収される電磁放射の特性分布を指します。電磁スペクトルを測定するために使用される機器は、分光器または分光計と呼ばれます。可視スペクトルは、人間の目で見ることができる電磁スペクトルの一部です。可視光の波長は390～700 nmです。[ 4 ]化学元素または化合物の吸収スペクトルは、低エネルギー状態から高エネルギー状態への電子遷移により化合物によって吸収される入射放射線の周波数または波長のスペクトルです。放出スペクトルは、高エネルギー状態から低エネルギー状態への電子遷移により化合物によって放出される放射線のスペクトルを指します。

様々な光源から発せられる光には様々な色が含まれており、それぞれに明るさや強度があります。虹、あるいはプリズムは、これらの成分色を様々な方向に送り出し、異なる角度からそれぞれを見えるようにします。強度を周波数（各色の明るさを示す）に対してプロットしたグラフは、光の周波数スペクトルです。可視周波数がすべて均等に存在する場合、知覚される光の色は白となり、スペクトルは平坦な線になります。したがって、平坦な線状のスペクトルは、光を表すものであれ、他の種類の波動現象（例えば音や構造物の振動）を表すものであれ、一般的に白と呼ばれることがよくあります。

無線および電気通信では、周波数スペクトルを多くの異なる放送局間で共有できます。無線スペクトルは、電磁スペクトルのうち、300 GHz未満の周波数に対応する部分で、約1 mmより長い波長に相当します。マイクロ波スペクトルは、300 MHz (0.3  GHz )から300 GHzの周波数と、1メートルから1ミリメートルの波長に相当します。[ 5 ] [ 6 ]各ラジオ局およびテレビ局は、チャンネルと呼ばれる割り当てられた周波数範囲で電波を送信します。多くの放送局が存在する場合、無線スペクトルは、それぞれが別々の情報を運ぶすべての個別のチャンネルの合計で構成され、広い周波数スペクトルに分散されます。特定のラジオ受信機は、振幅 (電圧) と時間の単一の関数を検出します。次に、ラジオは同調回路またはチューナーを使用して単一のチャンネルまたは周波数帯域を選択し、その放送局からの情報を復調またはデコードします。各チャンネルの強度とチューナーの周波数の関係をグラフにすると、それがアンテナ信号の周波数スペクトルになります。

天体分光法では、吸収線と輝線の強度、形状、位置、そして連続スペクトル全体のエネルギー分布から、天体の多くの特性が明らかになります。 恒星の分類とは、恒星をその特徴的な電磁スペクトルに基づいて分類することです。スペクトル流束密度は、恒星などの光源のスペクトルを表すために使用されます。

放射測定法や測色法（より一般的には色彩科学）において、光源のスペクトルパワー分布（SPD）は、光源の各周波数または色によって寄与されるパワーの尺度である。光スペクトルは通常、可視スペクトルに沿った点（多くの場合31）で、周波数空間ではなく波長空間で測定されるため、厳密にはスペクトル密度ではない。分光光度計の中には1～2ナノメートルという細かい増分を測定できるものもあり、0.5nm未満の分解能を持つさらに高解像度の装置も報告されている。[ 7 ]これらの値は他の仕様を計算するために使用され、その後、光源のスペクトル属性を示すためにプロットされる。これは特定の光源の色特性を分析する際に役立つ。

質量スペクトル

タイタンの電離層の質量スペクトル

イオンの存在量を質量電荷比の関数としてプロットしたものを質量スペクトルといいます。質量スペクトルは質量分析計によって生成されます。[ 8 ]質量スペクトルは、原子や分子の量と質量を決定するために用いられます。タンデム質量分析法は分子構造を決定するために使用されます。

エネルギースペクトル

物理学において、粒子のエネルギースペクトルとは、粒子エネルギーの関数として表される粒子数または粒子ビームの強度です。エネルギースペクトルを生成する技術の例としては、アルファ粒子分光法、電子エネルギー損失分光法、質量分析イオン運動エネルギー分光法などが挙げられます。

変位

振動を含む振動変位もスペクトル的に特徴付けることができます。

音響測定

音響学において、スペクトログラムは、時間または他の変数の関数として音の周波数スペクトルを視覚的に表現したものです。

音源には、多くの異なる周波数が混在することがあります。楽音の音色は、その倍音スペクトルによって特徴付けられます。私たちの周囲にある、いわゆるノイズと呼ばれる音には、多くの異なる周波数が含まれています。可聴周波数帯域全体に均等に分布する全ての可聴周波数が混在する音信号は、ホワイトノイズと呼ばれます。[ 12 ]

スペクトルアナライザは、音符の音波を構成周波数の視覚的表示に変換できる機器です。この視覚的表示は音響スペクトログラムと呼ばれます。ソフトウェアベースのオーディオスペクトルアナライザは低価格で入手可能で、業界の専門家だけでなく、研究者、学生、愛好家にも容易に利用できます。スペクトルアナライザによって生成される音響スペクトログラムは、音符の音響特性を提供します。基本周波数とその倍音を明らかにすることに加えて、スペクトログラムは音符の 時間的なアタック、ディケイ、サステイン、リリースの分析にも役立ちます。

連続スペクトルと離散スペクトル

白熱電球の連続スペクトル（中央）と蛍光灯の離散スペクトル線（下）

物理学では、物理量（エネルギーなど）のスペクトルは、スペクトル領域全体（周波数や波長など）にわたってゼロでない場合は連続的と呼ばれ、スペクトルバンドまたはスペクトル線のペアの間にバンドギャップがあり、独立変数上の離散的な集合でのみゼロでない値をとる場合は離散的と呼ばれます。[ 13 ]

連続スペクトルの古典的な例は、その名前の由来であり、励起された水素原子が放出する光のスペクトルのうち、自由電子が水素イオンに結合して光子を放出することによって生じる部分です。この光子は、電子が何らかの束縛量子状態からより低いエネルギーの状態に移行するときに生じる離散的なスペクトルとは対照的に、広い範囲の波長にわたって滑らかに広がっています。この古典的な例のように、この用語は、物理量の値の範囲が連続部分と離散部分の両方を（同時または異なる状況で）持つ可能性がある場合に最もよく使用されます。量子システムでは、連続スペクトル（制動放射線や熱放射など）は通常、気体中の原子、電子ビーム中の電子、金属の伝導帯電子などの自由粒子に関連付けられます。特に、自由粒子の位置と運動量は連続スペクトルを持ちますが、粒子が限られた空間に閉じ込められると、そのスペクトルは離散的になります。

多くの場合、連続スペクトルは、結晶内のフォノンのように、値が近すぎて区別できない離散スペクトルの便利なモデルにすぎない場合があります。

物理システムの連続スペクトルと離散スペクトルは、関数解析において、ハミルトン演算子などの関数空間に作用する線形演算子のスペクトルの分解における異なる部分としてモデル化できます。

離散スペクトル（この用語が最初に使われた用語）の典型的な例は、化学元素の孤立原子の発光スペクトルと吸収スペクトルに見られる、特定の波長の光のみを吸収・放出する特徴的な離散スペクトル線のセットです。分光法の技術はこの現象に基づいています。

離散スペクトルは、振動する弦、金属空洞内のマイクロ波、脈動する星の音波、高エネルギー粒子物理学における共鳴など、他の多くの現象にも見られます。物理系における離散スペクトルの一般的な現象は、関数解析のツール、具体的には関数空間に作用する線型作用素のスペクトルの分解によって数学的にモデル化することができます。

古典力学では

古典力学において、離散スペクトルはしばしば境界のある物体または領域における波動や振動と関連付けられます。数学的には、それらは、ある連続変数（例えばひずみや圧力）の発展を時間および／または空間の関数として記述する微分作用素の固有値と同一視することができます。

離散スペクトルは、関連する量が非正弦波の波形を持つ非線形振動子によっても生成される。注目すべき例としては、哺乳類の声帯から発せられる音が挙げられる。[ 14 ] [ 15 ] : p.684 やコオロギの鳴き声器官[ 16 ]は、そのスペクトルが振動周波数の整数倍（高調波）の周波数で一連の強い線を示す。

関連する現象として、正弦波信号（単一のスペクトル線からなる究極の「離散スペクトル」を持つ）が非線形フィルタによって変更されたときに強い高調波が出現するという現象がある。たとえば、純音が過負荷の増幅器を通して再生されたとき、[ 17 ]や強力な単色レーザービームが非線形媒体を通過したときなどである。[ 18 ] 後者の場合、周波数fとgを持つ2つの任意の正弦波信号を一緒に処理すると、出力信号は通常、周波数| mf + ng |でスペクトル線を持つことになる（mとnは任意の整数）。

量子力学では

量子力学では、観測可能なものの離散スペクトルとは、その観測可能なものをモデル化するために使用される演算子の固有値の純粋な点スペクトルを指す。[ 19 ] [ 20 ]

離散スペクトルは通常、何らかの意味で束縛された（数学的にはコンパクト空間に閉じ込められた）系に関連付けられます。位置演算子と運動量演算子は無限領域では連続スペクトルを持ちますが、コンパクト領域では離散（量子化）スペクトルを持ち、角運動量、ハミルトニアン、その他の量子系演算子にも同様のスペクトル特性が当てはまります。

量子調和振動子と水素原子は、ハミルトニアンが離散スペクトルを持つ物理系の例である。水素原子の場合、スペクトルは連続部分と離散部分の両方を持ち、連続部分は電離を表す。

  • 水素の発光スペクトルの離散部分
    水素の発光スペクトルの離散部分
  • 大気上（黄色）と海面（赤色）の太陽光のスペクトル。離散部分（O 2 による線など）と連続部分（H 2O と表示された帯など）を持つ吸収スペクトルを示しています。
    大気圏上空（黄色）と海面（赤色）の太陽光スペクトル。吸収スペクトルには不連続部分（Oによる線など）が見られる。2）と連続部分（ Hとラベル付けされたバンドなど）2O )
  • 重水素ランプから放射される光のスペクトル。離散的な部分（高く鋭いピーク）と連続的な部分（ピーク間の滑らかな変化）が見られる。小さなピークと谷は、離散的なスペクトル線ではなく、測定誤差によるものである可能性がある。
    重水素ランプから放射される光のスペクトル。離散的な部分（高く鋭いピーク）と連続的な部分（ピーク間の滑らかな変化）が見られる。小さなピークと谷は、離散的なスペクトル線ではなく、測定誤差によるものである可能性がある。

参照

参考文献

  1. ^オープンアクセスアイコン OpenStax Astronomy、「天文学における分光法」。OpenStax CNX。2016年9月29日。「OpenStax CNX」。2017年2月17日時点のオリジナルよりアーカイブ。 2017年2月17日閲覧。
  2. ^ニュートン、アイザック (1671). 「アイザック・ニュートン氏の手紙…光と色に関する彼の新しい理論を含む…」ロンドン王立協会哲学紀要6 (80): 3075– 3087. Bibcode : 1671RSPT....6.3075N . doi : 10.1098/rstl.1671.0072 .光線の屈折または回折によって生成される色の帯を表す「スペクトル」という単語は、 3076 ページで初めて登場します。
  3. ^ 「電磁スペクトル」 . Imagine the Universe! Dictionary . NASA. 2015年5月24日時点のオリジナルよりアーカイブ。 2015年6月3日閲覧。
  4. ^スター、セシー（2005年）『生物学：概念と応用』トムソン・ブルックス／コール社、  p.94、ISBN 0-534-46226-X。
  5. ^ポザール、デビッド・M. (1993).マイクロ波工学アディソン・ウェズリー出版社. ISBN 0-201-50418-9。
  6. ^ Sorrentino, R. および Bianchi, Giovanni (2010) Microwave and RF Engineering Archived August 5, 2016, at the Wayback Machine , John Wiley & Sons, p. 4, ISBN 047066021X。
  7. ^ Noui, Louahab; Hill, Jonathan; Keay, Peter J; Wang, Robert Y; Smith, Trevor; Yeung, Ken; Habib, George; Hoare, Mike (2002-02-01). 「バイオプロセスのアットラインモニタリングのための高解像度UV分光光度計の開発」 .化学工学およびプロセス：プロセス強化. 41 (2): 107– 114. Bibcode : 2002CEPPI..41..107N . doi : 10.1016/S0255-2701(01)00122-2 . ISSN 0255-2701 . 
  8. ^ IUPAC ,化学用語集、第5版（「ゴールドブック」）（2025年）。オンライン版：（2006年以降）「質量スペクトル」。doi：10.1351/goldbook.M03749
  9. ^ Munk, Walter H. (2010). 「波の起源と生成」. Coastal Engineering Proceedings . 1 : 1. doi : 10.9753/icce.v1.1 .
  10. ^ 「Datums - NOAA Tides & Currents」tidesandcurrents.noaa.gov . 2013年12月. 2022年12月6日時点のオリジナルよりアーカイブ。 2023年3月22日閲覧。
  11. ^ 「より正確なフーリエ変換」 SourceForge 、 2015年7月7日。 2023年3月22日閲覧。
  12. ^ 「ホワイトノイズの定義」 . yourdictionary.com . 2015年6月30日時点のオリジナルよりアーカイブ。
  13. ^ "連続スペクトル - klinics.lib.kmutt.ac.th" . KMUTT: Thailands Science General . 2 (1): 22. 2022年8月20日時点のオリジナル(PDF)からのアーカイブ – KMUTT経由。物理学において、連続スペクトルは通常、何らかの物理量（エネルギーや波長など）の達成可能な値の集合を意味し、実数の区間として最もよく説明されます。これは離散スペクトルの反対で、離散スペクトルは数学的な意味で離散的であり、各値の間に正のギャップがある達成可能な値の集合です。
  14. ^ Hannu Pulakka (2005),「逆フィルタリング、高速イメージング、電気声門図法を用いた人間の音声生成の分析」ヘルシンキ工科大学修士論文。
  15. ^リンドブロム、ビョルン、サンドバーグ、ヨハン (2007). 「音声と歌唱における人間の声」.シュプリンガー・ハンドブック・オブ・アコースティックス. ニューヨーク: シュプリンガー・ニューヨーク. pp.  669– 712. doi : 10.1007/978-0-387-30425-0_16 . ISBN 978-0-387-30446-5。
  16. ^ Popov, AV; Shuvalov, VF; Markovich, AM (1976). 「コオロギ（Gryllus bimaculatus）の鳴き声のスペクトル、音走性、および聴覚系」. Neuroscience and Behavioral Physiology . 7 (1). Springer Science and Business Media LLC: 56– 62. doi : 10.1007/bf01148749 . ISSN 0097-0549 . PMID 1028002. S2CID 25407842 .   
  17. ^ Paul V. Klipsch (1969)、「スピーカーの変調歪み」、 Wayback Machineに 2016 年 3 月 4 日にアーカイブ、Audio Engineering Society 誌。
  18. ^ Armstrong, JA; Bloembergen, N.; Ducuing, J.; Pershan, PS (1962-09-15). 「非線形誘電体における光波の相互作用」 . Physical Review . 127 (6). American Physical Society (APS): 1918– 1939. Bibcode : 1962PhRv..127.1918A . doi : 10.1103/physrev.127.1918 . ISSN 0031-899X . 
  19. ^ Simon, B. (1978). 「厳密な散乱理論の概要」p. 3. S2CID 16913591 . {{cite web}}:欠落または空|url=(ヘルプ)
  20. ^ Teschl, G. (2009). 「5.2 RAGE定理」.量子力学における数学的手法(PDF) . プロビデンス、ロードアイランド州: アメリカ数学協会. ISBN 978-0-8218-4660-5。
「 https://en.wikipedia.org/w/index.php?title=Spectrum_(physical_sciences)&oldid=1323903932」より取得