ジグザグ補題

数学、特にホモロジー代数において、ジグザグ補題は、特定の鎖複体のホモロジー群に特定の長完全列が存在することを主張する。この結果はあらゆるアーベル圏において成立する。これはマイヤー・ヴィートリス列の一般化とみなすことができる。

声明

アーベル範疇（アーベル群の範疇や与えられた体上のベクトル空間の範疇など）において、と を次の短い完全列に適合する鎖複体とする。 ${\displaystyle ({\mathcal {A}},\partial _{\bullet }),({\mathcal {B}},\partial _{\bullet }')}$ ${\displaystyle ({\mathcal {C}},\partial _{\bullet }'')}$

${\displaystyle 0\longrightarrow {\mathcal {A}}\mathrel {\stackrel {\alpha }{\longrightarrow }} {\mathcal {B}}\mathrel {\stackrel {\beta }{\longrightarrow }} {\mathcal {C}}\longrightarrow 0}$

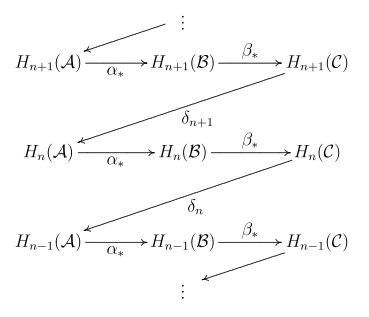
このようなシーケンスは次の可換図の省略形です。

ここで、行は正確なシーケンスであり、各列はチェーン複素数です。

ジグザグ補題は境界写像の集合が存在することを主張する。

${\displaystyle \delta _{n}:H_{n}({\mathcal {C}})\longrightarrow H_{n-1}({\mathcal {A}}),}$

これにより、次のシーケンスが正確になります。

写像と写像は、ホモロジーによって誘導される通常の写像です。境界写像については後述します。この補題の名前は、列内の写像が「ジグザグ」に振舞うことに由来します。ジグザグ補題の変形は、一般に「スネーク補題」として知られています（これは、以下に示すジグザグ補題の証明のエッセンスを抽出しています）。 ${\displaystyle \alpha _{*}^{}}$ ${\displaystyle \beta _{*}^{}}$ ${\displaystyle \delta _{n}^{}}$

境界地図の作成

写像は標準的な図式追跡論を用いて定義される。を の類とすると、 となる。行の正確性は が射影的であることを意味するので、 を満たすものが存在するはずである。図式の可換性により、 ${\displaystyle \delta _{n}^{}}$ ${\displaystyle c\in C_{n}}$ ${\displaystyle H_{n}({\mathcal {C}})}$ ${\displaystyle \partial _{n}''(c)=0}$ ${\displaystyle \beta _{n}^{}}$ ${\displaystyle b\in B_{n}}$ ${\displaystyle \beta _{n}^{}(b)=c}$

${\displaystyle \beta _{n-1}\partial _{n}'(b)=\partial _{n}''\beta _{n}(b)=\partial _{n}''(c)=0.}$

正確に言えば、

${\displaystyle \partial _{n}'(b)\in \ker \beta _{n-1}=\mathrm {im} \;\alpha _{n-1}.}$

したがって、 は単射なので、となる唯一の元が存在する。は単射であり、 となる ので、これは循環である。${\displaystyle \alpha _{n-1}^{}}$ ${\displaystyle a\in A_{n-1}}$ ${\displaystyle \alpha _{n-1}(a)=\partial _{n}'(b)}$ ${\displaystyle \alpha _{n-2}^{}}$

${\displaystyle \alpha _{n-2}\partial _{n-1}(a)=\partial _{n-1}'\alpha _{n-1}(a)=\partial _{n-1}'\partial _{n}'(b)=0,}$

なので、 となる。つまり、 は循環的であることを意味するので、 のクラスを表す。ここで定義できる。 ${\displaystyle \partial ^{2}=0}$ ${\displaystyle \partial _{n-1}(a)\in \ker \alpha _{n-2}=\{0\}}$ ${\displaystyle a}$ ${\displaystyle H_{n-1}({\mathcal {A}})}$

${\displaystyle \delta _{}^{}[c]=[a].}$

境界写像が定義されていれば、それらが明確に定義されている（つまり、cとbの選択に依存しない）ことを示すことができる。証明には、上記と同様の図式追跡の議論が用いられる。このような議論は、各群におけるホモロジーの配列が完全であることを示す際にも用いられる。

参照

• マイヤー・ヴィエトリス配列

参考文献

• ハッチャー、アレン（2002年）『代数的位相幾何学』ケンブリッジ大学出版局、ISBN 0-521-79540-0。
• ラング、セルジュ（2002）、代数学、大学院数学テキスト、第211巻（改訂第3版）、ニューヨーク：シュプリンガー・フェアラーク、ISBN 978-0-387-95385-4、MR  1878556
• マンクレス、ジェームズ・R. (1993). 『代数的位相幾何学の要素』 ニューヨーク: ウェストビュー・プレス. ISBN 0-201-62728-0。