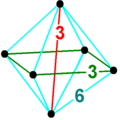
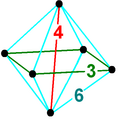
八面体ピラミッド

四角錐
四角錐
タイプ	多面体ピラミッド
シュレーフリ記号	( ) ∨ [( ) ∨ {4}] [( )∨( )] ∨ {4} = { } ∨ {4} { } ∨ [{ } × { }] { } ∨ [{ } + { }]
細胞	2 ( )∨{4} 4 ( )∨{3}
顔	12 {3} 1 {4}
エッジ	13
頂点	6
対称群	[4,1,1]、次数8 [4,2,1]、次数16 [2,2,1]、次数8
デュアル	自己双対
プロパティ	凸面、正面

八面体ピラミッド
八面体ピラミッド
	シュレーゲル図
タイプ	多面体ピラミッド
シュレーフリ記号	( ) ∨ {3,4} ( ) ∨ r{3,3} ( ) ∨ s{2,6} ( ) ∨ [{4} + {}] ( ) ∨ [{} + {} + {}]
細胞	1 {3,4} 8 ( ) ∨ {3}
顔	20 {3}
エッジ	18
頂点	7
対称群	B 3 , [4,3,1], 次数 48 [3,3,1], 次数 24 [2 + ,6,1], 次数 12 [4,2,1], 次数 16 [2,2,1], 次数 8
デュアル	立方ピラミッド
プロパティ	凸、正則セル、ブラインド多面体

4次元幾何学において、正八面体ピラミッドは、底面に1つの正八面体、そして頂点で交わる8つの三角錐セルによって囲まれています。正八面体の外接半径は辺の長さで割った値よりも小さいため、 ^{[ 1 ]}適切な高さを計算することで、正四面体のように正四面体のように正四面体として三角錐を作成できます。

全てのセルが正方格子であるため、ブラインド多面体です。2つのコピーを追加することで、同じくブラインド多面体である八面体両錐体を作成できます。

八面体ピラミッドの出現

正16セルは、すべての頂点の周りに正八面体ピラミッドを持ち、正八面体は16セルの中心を通ります。したがって、2つの正八面体ピラミッドを底辺同士で並べると、16セルが構成されます。16セルは、16セルハニカムのように4次元空間をモザイク状に並べます。

4次元空間の頂点（各ピラミッドの頂点）の周りには、ちょうど24個の正八面体ピラミッドが収まります。この構成により、正八面体の境界セルを持つ24セルが生成され、中心頂点を24辺の長さの長半径で囲みます。単位辺長の24セルの4次元コンテンツは2であるため、正八面体ピラミッドのコンテンツは1/12です。24セルは、24セルのハニカム構造のように4次元空間をモザイク状に分割します。

八面体ピラミッドは、切断された5-オルソプレックスの頂点図形である。。

八面体ピラミッドのグラフは、平面被覆を持つ連結グラフはそれ自体が射影平面であるという根上の予想に対する唯一の可能な最小の反例である。 ^[²^]

4 次元座標の例。立方体の最初の 3 つの座標に 6 つのポイントがあり、頂点に 4 番目の次元があります。 ${\begin{array}{lllr}(\pm 1,&0,&0;&0)\\(0,&\pm 1,&0;&0)\\(0,&0,&\pm 1;&0)\\(0,&0,&0;&\ 1)\end{array}}$

その他の多面体

立方ピラミッド

八面体ピラミッドの双対は立方体ピラミッドで、立方体の底面と頂点で交わる6 つの四角錐として見られます。

4 次元座標の例。立方体の最初の 3 つの座標に 8 つのポイントがあり、頂点に 4 番目の次元があります。 ${\begin{array}{lllr}(\pm 1,&\pm 1,&\pm 1;&0)\\(0,&0,&0;&1)\end{array}}$

四角錐

正方錐（）∨ [（）∨ {4}] ）は、二等分された八面体錐である。正方錐の底面と、頂点で交わる4つの四面体と、もう1つの正方錐を持つ。また、辺心投影では、共通の辺を4つの四面体が囲む正方双錐として見ることもできる。2つの頂点の高さが同じ場合、より高い対称性を持つ名前[（）∨ ( )] ∨ {4} = { } ∨ {4} が与えられ、辺と垂直な正方形が結合する。^{[ 3 ]}

正方錐は、長方錐、{}∨[{}×{}]、または菱形錐、{}∨[{}+{}]、またはその他の対称性の低い形式に変形できます。

正方錐は、次のような形の一様多面体の頂点図形として存在する。これには、ビットトランケート 5 オルソプレックスとビットトランケートテッセラティックハニカムが含まれます。