チェックメイト

チェックメイト(しばしばメイトと略される)とは、チェスやチェスに似たゲームにおいて、プレイヤーのキングがチェック(捕獲の脅威)を受けており、脱出の見込みがない局面を指します。相手がチェックメイトすれば勝ちとなります。
チェスでは、キングが実際に捕獲されることはありません。キングがチェックメイトされた時点で負けとなります。正式なゲームでは、負けが確定したゲームでは、チェックメイトされる前に投了するのが良いエチケットとされています。[ 1 ] [ 2 ]
プレイヤーがチェックを受けていないが、有効な手がない場合は、ステイルメイトとなり、ゲームは直ちに引き分けで終了します。チェックメイトの手は、ハッシュ記号「#」を用いて代数記法で記録されます。例:34.Qg3#
例
チェックメイトは、片側で全ての駒が盤上に残っている状態でわずか2手で発生する場合(ゲームの序盤のフールズメイトのように)、中盤の位置で発生する場合(1956年のドナルド・バーンとボビー・フィッシャーの間で行われた世紀の対局のように)、または終盤の位置でわずか3つの駒で多くの手で発生する場合がある。
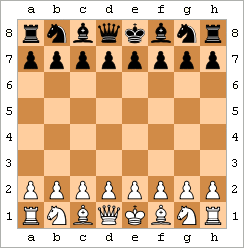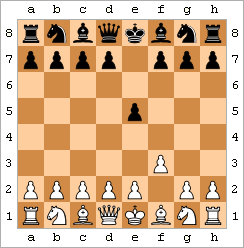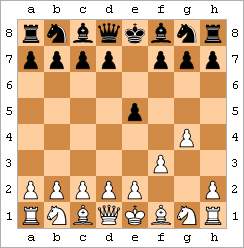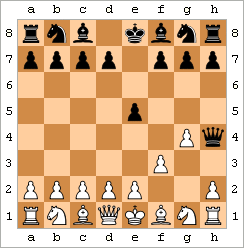
D.バーン対フィッシャー
白は41...Rc2#の後にチェックメイトされる。[ 5 ] | ルークでチェックメイト
黒はチェックメイトです。[ 6 ] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
語源
バーンハート語源辞典によると、チェックメイトという用語はペルシャ語の「シャー・マート」(شاه مات)が変化したもので、「王は無力である」という意味である。[ 7 ]ペルシャ語の「マート」は王を指すが、サンスクリット語の「マータ」(māta)も「マート」と発音し、対戦相手によって王国が「徹底的に横断され、測られ、計り知れ」たことを指す。「マータ」は動詞語源「マー」の過去分詞である。[ 8 ]チェスはアラブ世界を経由してヨーロッパに伝わったため、「王は死んだ」という意味だと主張する者もいる。アラビア語のマータ(مَاتَ)は「死んだ」または「死んでいる」という意味である。[ 9 ] [ 10 ]モガダムはメイトという言葉の語源を解明した。これはペルシア語の動詞「マンダン」(ماندن)に由来し、「残る」という意味で、ラテン語の「マンネオ」、ギリシャ語の「メノー」(μένω、「私は残る」)と同義である。これは「見捨てられた」という意味で「残った」を意味し、正式な翻訳は「驚かされた」であり、軍事的な意味で「待ち伏せされた」を意味する。[ 11 ]「シャー」(شاه)はペルシア語で君主を意味する。プレイヤーはキングがチェック状態にあるとき「シャー」と宣言する。「マート」(مات)はペルシア語で「途方に暮れた」「無力な」「敗北した」という意味の形容詞である。つまり、キングが待ち伏せされ、途方に暮れ、無力な、敗北した、あるいは運命に見放されたとき、メイト状態にあるのである。 [ 12 ]
現代ペルシア語で「マテ」という言葉は、凍りつき、口を開けて見つめ、混乱し、反応しない人物を描写します。これは「呆然とした」や「呆然とした」という言葉と密接な関連があります。したがって、別の解釈として、「マテ」を「反応できない」と解釈することも可能です。キングがマテ(シャーマット)状態にあるということは、キングが反応できないことを意味し、これは相手の最後の手に対してプレイヤーのキングが反応できないことを意味します。この解釈は、キングを殺すことではなく、降伏以外に有効な反応を残さないという、このゲームの本来の意図に非常に近いものであり、シャー・ナーメに詳述されている起源の物語とより一致しています。
現代の用語では、 「チェックメイト」という言葉は、反駁できない戦略的な勝利の比喩である。 [ 13 ]
歴史
初期のサンスクリットチェス( 500年頃~700年頃)では、キングを捕獲することでゲームが終了しました。ペルシャ人(700年頃~800年頃)は、キングが攻撃を受けていることを警告する(現代の用語で「チェック」と表現する)という概念を導入しました。これは、ゲームの早期かつ偶発的な終了を避けるためでした。後にペルシャ人は、キングをチェックに動かしたり、チェックされたままにしたりできないという追加のルールを追加しました。その結果、キングを捕獲することはできなくなり、[ 14 ]チェックメイトがゲームを終わらせる唯一の決定的な方法となりました。[ 15 ]
1600年頃までは、相手の駒をすべて取り、キングだけを残すことでも勝利することができました。このスタイルのゲームは現在、アニヒレーション(殲滅)またはロバド(ロバド)と呼ばれています。[ 16 ]中世になると、チェックメイトで勝つ方がより高貴な勝利であると考えるようになり、アニヒレーションはしばらくの間、半勝とみなされるようになりましたが、その後廃止されました。[ 15 ]
2つの主要な部分
 |  |  |  |
2 つの主要な駒(クイーンまたはルーク)は、ラダー チェックメイトと呼ばれるテクニックを使用して、簡単に盤の端でチェックメイトを強制できます。[ 17 ]この手順では、2 つの駒を隣接する列または列に置き、一方の駒でキングをチェックし、もう一方の駒でキングが盤を上がるのを阻止することで、キングを盤の端に追い込みます。[ 18 ]図では、白が黒のキングを 1 列ずつ端に追い込むことでチェックメイトしています。ラダー チェックメイトは、2 つのルーク、2 つのクイーン、またはルークとクイーンでチェックメイトするために使用できます。[ 18 ]

基本的なチェックメイト
片側がキングのみで、もう片側がチェックメイトを強制するのに必要な最小限の駒しか持っていない場合、基本的なチェックメイトは4つあります。すなわち、(1)クイーン1個、(2)ルーク1個、(3)反対色のマスにビショップ2個、(4)ビショップ1個とナイト1個です。これらのチェックメイトはすべて、キングの助けによって成立します。[ 20 ] 勝っている側がより多くの駒を持っている場合、チェックメイトはより容易になります。
クイーンによるチェックメイトは最も一般的で、最も簡単に達成できます。これは、ポーンがクイーンになった後によく発生します。ルークによるチェックメイトも一般的ですが、ビショップ2つ、またはビショップとナイトによるチェックメイトはまれです。ビショップ2つのチェックメイトは比較的簡単に達成できますが、ビショップとナイトのチェックメイトは難しく、正確さが求められます。
王と女王
 |  |  |
最初の2つの図は、盤上のどの辺でも起こり得る、クイーンによる基本的なチェックメイトの局面の代表例を示しています。当然のことながら、正確な位置は図と異なる場合があります。最初のチェックメイトの局面では、クイーンは相手のキングの真正面にあり、白のキングはクイーンを守っています。2つ目のチェックメイトの局面では、キング同士が向かい合い、クイーンはキングの列(または列)でメイトします。
サポートメイト
白のキングはf6かg6にあることもあります。[ 21 ] | 直角三角形のメイト
女王はマークされたマス目に置くこともできます。[ 22 ] | 追い詰められた仲間
女王はマークされたマス目に置くこともできます。[ 22 ] |
| 1つの | b | c | d | e | f | グラム | h | ||
| 8 |     | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| 1つの | b | c | d | e | f | グラム | h | ||
クイーンがある側が動く場合、どちらの側も最適なプレイをすれば、どの開始位置からでも最大10手でチェックメイトを強制できますが、通常はそれよりも少ない手数で済みます。[ 23 ] [ 24 ]ポーンがクイーンに昇格したばかりの位置では、最大9手が必要です。[ 25 ]
図に示すポジションでは、白は黒のキングを長方形の中に閉じ込め、その長方形を縮小してキングを盤の端に 追いやることで簡単にチェックメイトします。
- 1. Qf6 Kd5 2. Qe7 Kd4 3. Kc2 Kd5 4. Kc3 Kc6 5. Kc4 Kb6 6. Qd7 Ka6 7. Qb5+ [ a ] Ka7 8. Kc5 Ka8 9. Kc6 Ka7 10. Qb7 # [ 26 ]
膠着状態を避ける
勝っている側は相手のキングをステイルメイトさせないように注意する必要がありますが、守っている側はステイルメイトに陥りたいと考えます。ステイルメイトには一般的に5つの種類があり、強い側はこれらを避けなければなりません。最初の2つはより一般的です。[ 27 ]
黒が動けば膠着状態。白のキングが盤上のどこに置かれていても、クイーンは黒のあらゆる動きを封じます。 | ||||||||||||||||||||||||||||||||||||||||||||||||
キングとルーク
 |  |  |
ルークによる追い詰められたチェックメイト[ 28 ] |
最初の図は、ルークを使った基本的なチェックメイトの局面を示しています。これは盤のどの端でも起こり得ます。黒のキングは盤の端のどのマスにいてもよく、白のキングはそれに対向し、ルークは(捕獲されないことを前提として)横一列または横一列のどのマスからでもチェックメイトできます。2番目の図は少し異なる局面を示しています。キングは対向していませんが、守備側のキングは必ず角にいなければなりません。
ルークのある側が動く場合、どの開始位置からでも最大16手でチェックメイトを強制することができます。[ 27 ]繰り返しになりますが、キングとルーク対キングのメイトがどのように達成されるかについては 、 Wikibooks – Chess/The Endgame を参照してください。
3 番目の図の位置では、白は黒のキングを長方形の中に閉じ込め、その長方形を縮小してキングを盤の端に追いやることでチェックメイトします。
- 1. Kd3+ Kd5 2. Re4 Kd6 3. Kc4 ! Kc6 4. Re6+ Kc7 5. Kc5 Kd7 6. Kd5 Kc7 7. Rd6 Kb7 8. Rc6 Ka7 9. Kc5 Kb7 10. Kb5 Ka7 11. Rb6 Ka8 12. Kc6 Ka7 13. Kc7 Ka8 14. Ra6# (2番目のチェックメイトの位置、回転). [ 29 ]
膠着状態を避ける
膠着状態のパターンは2つある:[ 30 ]
黒が指す場合、これはステイルメイトです。白のキングはc7またはb6にいても構いません。 |
黒が動くと膠着状態になります。 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
国王と二人の司教
 |  |  |  |
2つのビショップによるチェックメイトとは、 1つのキングが相手の2つのビショップとキングによってチェックメイトされることである。 [ b ] 優勢な側は、1つのキングを追い詰め、2つのビショップとキングの協力によってチェックメイトを強制することができる。唯一の条件は、2つのビショップが反対色のマスに動かなければならないということである。[ c ] [ 32 ]チェックメイトを達成するには最大19手かかる。
キングとビショップは協力して敵のキングを盤の端に追い込み、さらに隅に追い込んで詰め寄る。[ 31 ]「このプロセスは少し長いですが、オープンボード上の2つのビショップの力を垣間見ることができるので興味深いです。」[ 33 ]
2つのビショップによるチェックメイトによって、3つの基本的なチェックメイトの位置が可能である。[ 34 ] 1つ目は、コーナーでのチェックメイトである。2つ目の位置は、コーナーのマス目の隣のサイドマスでのチェックメイトである(この位置は理論的にはエッジ沿いのどこにでも発生する可能性があるが、コーナーに隣接してのみ強制できる)。ビショップがある側で動かす場合、チェックメイトは最大19手で強制できるが[ 35 ] 、非常にまれな位置(可能な位置の0.03%)を除く。[ 36 ] 3つ目の位置は、コーナーでもその隣接するサイドマスでもないエッジマスでキングをチェックメイトすることであるが、これは可能だが強制はできない。[ 34 ]
2人のビショップがキングの助けを借りてチェックメイトを強いるのはそれほど難しくありません。2つの原則が適用されます。
- ビショップは盤の中央付近、かつ隣接する対角線上に配置するのが最も効果的です。これにより、相手のキングを遮断できます。
- キングはビショップと組み合わせて積極的に使用する必要があります。
セイラワンより
2 つのビショップとキングは、メイトを強制できます。 | |||||||||||||||||||||||||||||||||||||||||||||
セイラワンの局面では、白はまず黒のキングを盤の端に追い込み、次に角に追い込み、そしてチェックメイトすることで勝ちます。これは盤のどの辺、どの角でも構いません。手順は以下のとおりです。
- 1. Ke2 Ke4 (黒はキングを中央近くに維持しようとする) 2. Be3 Ke5 (キングを強制的に押し戻す。よくある手だ) 3. Kd3 Kd5 4. Bd4 Ke6 5. Ke4 Kd6 (黒は中央近くに留まるために別のアプローチを試みる) 6. Bc4 (白は良いポジションにいる。ビショップは中央にあってキングはアクティブ) 6... Kc6 (黒はサイドに行くのを避けている) 7. Ke5 Kd7 (黒は a8 の角を避けようとしている) 8. Bd5 (黒のキングを c6 に近づけないようにしている) 8... Kc7 9. Bc5 Kd7 10. Bd6! (キングを盤の端に追いやる重要な手) 10... Ke8 (黒はまだ角を避けている) 11. Ke6 (黒のキングは盤の端から離れられない) 11... Kd8 12. Bc6 (キングを角に追いやる) 12... Kc8 (黒のキングは c8 と d8 に限定される; 白のキングは a7 と b7 をカバーする必要がある) 13. Kd5 (13. Ke7 ?は膠着状態) 13... Kd8 14. Kc5 Kc8 15. Kb6 Kd8 (白はキングが角に動くのを許さなければならない) 16. Bc5 Kc8 17. Be7! (キングを角に追いやる重要な手) 17... Kb8 18. Bd7!(前手と同じ原理)18... Ka8 19. Bd8 (白はテンポを放棄する手を取らなければならない。この手は、Bc5、Bf8、Be6、またはKa6とともにそのような手である)19... Kb8 20. Bc7+ Ka8 21. Bc6#(このセクションの最初の図と同じ)。[ 37 ]
これは、この局面から強制的にチェックメイトを成立させる最短の方法ではありません。ミュラーとランプレヒトは15手で解決する方法を提示していますが、黒の手が不正確である点が指摘されています(終盤表によると)。[ 35 ]
膠着状態を避ける
| 1つの | b | c | d | e | f | グラム | h | ||
| 8 |       | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| 1つの | b | c | d | e | f | グラム | h | ||
ステイルメイトの一例はこのポジションで、1.Kb6(x印)はステイルメイトとなる。[ 38 ]
王、司教、騎士
 |  |  |  |
基本的なチェックメイトの中で、これは最も強制が難しいものです。なぜなら、この2つの駒は敵キングに対して遠距離から直線的な障壁を形成できないからです。また、チェックメイトはビショップが支配するコーナーでのみ強制可能です。[ 36 ] [ 39 ]
ビショップとナイトによるチェックメイトの基本的なポジションが2つ、またはビショップとナイトによるチェックメイトが2つ示されています。[ 40 ]最初のポジションはビショップによるチェックメイトで、黒のキングがコーナーにあります。ビショップは対角線上の他のマス目にいてもよく、白のキングとナイトは g8 と h7 を攻撃するマス目になければなりません。2番目のポジションはナイトによるチェックメイトで、黒のキングがコーナーに隣接するサイドマス目にあります。ナイトは黒のキングをチェックする他のマス目にいても構いません。白のキングはビショップを守り、ナイトがカバーしていないマス目をカバーするマス目になければなりません。
ビショップとナイトを持つ側が指す場合、どの開始位置からでも最大33手でチェックメイトを強制することができます[ 41 ]。ただし、守備側のキングが最初にビショップとナイトをフォークし、両方を守れない場合を除きます。しかし、チェックメイトのプロセスには正確なプレイが求められます。わずかなミスでも、 50手ルールによる引き分けやステイルメイトにつながる可能性があるからです。
プレイヤーがこのチェックメイトの手順を学ぶべきかどうかについては意見が分かれている。 ジェームズ・ハウエルは、稀にしか起こらないため、2つのビショップによるチェックメイトを著書から省いているが、ビショップとナイトによるチェックメイトは含めている。ハウエルは、自身もこのチェックメイトを3回(常に防御側)経験しており、2つのビショップによるチェックメイトよりも頻繁に起こると述べている。[ 42 ] 一方、ジェレミー・シルマンは、2つのビショップによるチェックメイトは含めているものの、ビショップとナイトによるチェックメイトは含めていない。なぜなら、自身は一度しか経験しておらず、友人のジョン・ワトソンは一度も経験していないからである。[ 43 ]シルマンは、「…このチェックメイトを習得するにはかなりの時間がかかるだろう。チェスを志す者が、生涯で(せいぜい)1、2回しか達成できないような終盤の習得に、チェスの勉強に割いている貴重な時間を本当に費やすべきだろうか?」と述べている。
膠着状態を避ける
| 1つの | b | c | d | e | f | グラム | h | ||
| 8 |      | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| 1つの | b | c | d | e | f | グラム | h | ||
この局面は、AHブラントンによる1966年の終盤研究の末尾にあるステイルメイトの例です。白は1.Na3+? と指したところです。黒が1...Kc1! と指した場合、白はビショップを動かさなければなりません。なぜなら、ビショップが捕獲されると、物資不足ルールにより引き分けとなるからです。しかし、ビショップが動いた後は、ステイルメイトとなります。[ 44 ]
一般的なチェックメイト
後列の仲間
| 1つの | b | c | d | e | f | グラム | h | ||
| 8 |         | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| 1つの | b | c | d | e | f | グラム | h | ||
後列チェックメイトとは、ルークまたはクイーンが後列(ゲーム開始時に駒(ポーンではない)が立っている列)に沿って成立させたチェックメイトであり、メイトされたキングは2列目の味方駒(通常はポーン)によってブロックされているため、盤上で前進することができない。[ 45 ]図は後列チェックメイトの例を示している。これはコリドーメイトとも呼ばれる。
学者の仲間
学者のメイト(4 手でチェックメイトとも呼ばれる) は、次の手順で達成されるチェックメイトです。
手順は異なる順序で、またはわずかに変化して実行される場合もありますが、基本的な考え方は同じです。クイーンとビショップがf7(黒がチェックメイトを実行している場合はf2)で単純なチェックメイト攻撃を行います。[ 46 ] 4手でチェックメイトする方法は他にもあります。
愚か者の仲間
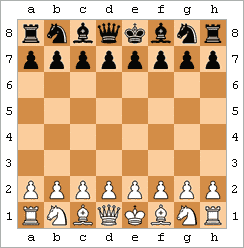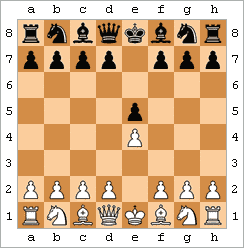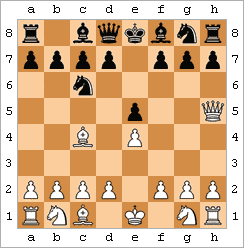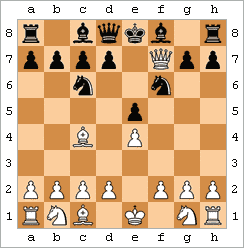
愚者の詰みは、2手詰みとも呼ばれ、最も速い詰みです。代表的な例として、以下の手順が挙げられます。
結果として、図のような局面となる。[ 47 ](このパターンには若干のバリエーションがあり、例えば白はf3の代わりにf4を打ったり、gポーンを先に動かしたり、黒は...e5の代わりに...e6を打ったりする可能性がある。)
窒息した仲間
27.Nf7+ Kg8 28.Nh6+ Kh8 29.Qg8+ Rxg8 30.Nf7# の後の詰み。 |
最終順位 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
スマザードメイトとは、ナイトが決めたチェックメイトのことであり、メイトされたキングは自身の駒に囲まれて(またはスマザードされて)動けない状態となる。 [ 49 ]
詰みは通常、盤の隅で見られます。これは、キングを囲むのに必要な駒の数が少ないためです。最も一般的な詰みの形は、隣の図に示されています。f7のナイトがh8のキングに詰みをかけますが、 g8のルークとg7およびh7のポーンによって詰みを逃れることができません。同様に、白はh1の白キングとf2のナイトに詰みをかけることができます。
まれなチェックメイト
 |  |  |  |
まれなポジションでは、キングとナイト対キングとポーンで強制的にチェックメイトすることが可能です。
スタマの仲間
| 1つの | b | c | d | e | f | グラム | h | ||
| 8 |      | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| 1つの | b | c | d | e | f | グラム | h | ||
スタンマの詰み(フィリップ・スタンマにちなんで名付けられた)を示す図では、白が勝つ:[ 50 ]
- 1. Nb4+ Ka1
- 2. Kc1 a2
- 3. Nc2#
黒が先に動いた場合も白が勝ちます。
- 1...カ1
- 2. Nc1 a2
- 3. Nb3#
| 1つの | b | c | d | e | f | グラム | h | ||
| 8 |      | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| 1つの | b | c | d | e | f | グラム | h | ||
このチェックメイトは、2001年キューバ選手権のヘスス・ノゲイラス対マイケル・ゴンゴラ戦で発生しました[ 51 ](図を参照)。
- 81. Kc2 Ka1
- 82. Nc5 Ka2
82...a2 の場合は 83.Nb3#。
- 83. Nd3
最初の図の位置に到達し、黒が動きます。
- 83...カ1
- 84. Nc1 1-0
黒はここで投了し、ゲームは84...a2 85.Nb3#と続行されたはずだった。[ 52 ]
| 1つの | b | c | d | e | f | グラム | h | ||
| 8 |      | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| 1つの | b | c | d | e | f | グラム | h | ||
ナイトが d2 にある同様の位置は、500 年以上前から存在し、ルカ・パチョーリの1498 年の著書『チェスのゲーム』(ラテン語で「チェスのゲーム」) の中で「Partito n. 23」として特定されています。この著書は最近、アボカ・ミュージアム・エディツィオーニによって再版 (Gli scacchi) されました。
- 1. Nf3 Ka1
- 2. Nd4 Ka2
- 3. Ne2 Ka1
- 4. Nc1 a2
- 5. Nb3#
珍しい仲間たち
キングとナイトがキングとビショップ、ナイト、またはルークをチェックメイトできる局面もあります。また、キングとビショップが、キングと、別の色のマスにあるビショップまたはナイトをチェックメイトできる局面もありますが、盤上に他の駒がない場合、チェックメイトを強制することはできません(例については図を参照してください)。[ 53 ]ただし、FIDEチェスルールでは、これらの駒の組み合わせが「駒不足」または「チェックメイト不可能」という理由で引き分けと判定されることを防いでいます。米国チェス連盟のルールは異なります。マイナーピース対マイナーピースの典型的な局面では、残り時間が限られている場合、プレイヤーは引き分けを主張することができます。[ 54 ]
パンドルフィーニ
チェックメイトだが強制はできない | パンドルフィーニ
チェックメイトだが強制はできない | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
パンドルフィーニ
チェックメイトだが強制はできない |
チェックメイトだが強制はできない |
チェックメイトだが強制はできない | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2人または3人の騎士
- 二人の騎士
 |  |  |  |
キング1枚とナイト2枚ではチェックメイトを強制することは不可能ですが、チェックメイトの局面は可能です(最初の図を参照)。2つ目の図では、黒が1...Ka8 ??と指した場合、白は2.Nbc7# でチェックメイトできますが、黒は1...Kc8 と指してこの脅威から逃れることができます。防御側の課題は簡単です。次の手でチェックメイトされる局面に入らないようにするだけで、そのような状況でも常に別の手が使えるのです。[ 55 ]
3つ目の図では、片方のナイトがc1をガードしており、もう片方のナイトがチェックメイトを狙っています。1.Ndc3+ Ka1の後、白はe2のナイトをc2に送る必要があります。しかし、白が2.Nd4と指せば、黒はステイルメイトになってしまいます。[ 56 ]
状況によっては、ナイト2体とキング1体で、キングとポーン(稀にポーンが複数)に対してチェックメイトを強いられることがあります。実際に実行するのは非常に難しいですが、勝利の戦略は、ナイト1体で敵のポーンを封鎖し、敵のキングを膠着状態に追い込み、もう1体のナイトをチェックメイトに持ち込むことです。[ 56 ](「ナイト2体による終盤」を参照)。
- 三人の騎士
 |  |  |  |  |
3人のナイトと1人のキングは、20手以内に1人のキングに対してチェックメイトを強制することができます(1人のキングがすぐにナイトを獲得できないと仮定)。[ 57 ]これらの状況は通常、チェスの問題 でのみ見られます。これは、ナイトの少なくとも1つは昇格した駒でなければならないためであり、ポーンをクイーン以外の駒に昇格させる理由はほとんどないからです(アンダープロモーションを参照)。
参照
注記
- ^ 7.Kc5 は 2 手早く勝ちます。
- ^「1人のナイトまたは1人のビショップに対しては、防御側はたとえ望んでも負けることはできない。」 [ 31 ]
- ^アンダープロモーションの場合にのみ、同じ色のマス目にビショップが出現します。
参考文献
- ^フーパー&ワイルド 1992、336ページ
- ^バージェス 2009、526ページ
- ^ 「D. バーン対フィッシャー、ニューヨーク 1956」 . Chessgames.com . 2022年9月17日閲覧。
- ^クルツドルファー 2003、92ページ
- ^バージェス、ナン、エムズ 2004、216ページ
- ^クルツドルファー 2003、144ページ
- ^ハーパー、ダグラス、ダン・マコーマック「オンライン語源辞典」 。 2010年5月29日閲覧。
- ^モニエ・ウィリアムズ サンスクリット語辞典
- ^フーパー&ワイルド 1992
- ^デイビッドソン 1949、70ページ
- ^デイヴィッドソン 1949年、70~71ページ
- ^マレー 2012、159ページ
- ^ 「チェックメイト – 無料のメリアム・ウェブスター辞書による定義と詳細」 Merriam-webster.com、2010年8月13日。 2012年6月18日閲覧。
- ^デイビッドソン 1949、22ページ
- ^ a bデイビッドソン 1949年、63~64ページ
- ^デイビッドソン、ヘンリー (2012). 『チェスの小史』 スリーリバーズ・プレス. ISBN 9780307828293。
- ^ Beauknowsin #chess • 3年前 (2017年10月26日). 「初心者のためのチェスレッスン #1 – ラダーチェックメイト!」 . Steemit . 2020年6月5日閲覧。
{{cite web}}: CS1 maint: 数値名: 著者リスト (リンク) - ^ a bパンドルフィーニ 1988、18–20 ページ
- ^シルマン 2007、7~8ページ
- ^シルマン 2007、33ページ
- ^パンドルフィニ 2009、22ページ
- ^ a bパンドルフィニ 2009、p. 23
- ^ファイン&ベンコー 2003、1-2 ページ
- ^ミュラー & ランプレヒト 2001、p. 16
- ^レヴィ&ニューボーン 1991、144ページ
- ^セイラワン 2003、4~5ページ
- ^ a bファイン&ベンコー 2003、p. 2
- ^パンドルフィニ 2009、36ページ
- ^セイラワン 2003、1~4ページ
- ^ファイン&ベンコー 2003、2–3 ページ
- ^ a b Fine 1979、1ページ。
- ^ Fine 1979、p. 4、「同じ色のビショップ2人はメイトを執行できません。メイトの位置は考えられません。同じことは、すべて同じ色のビショップが9人(またはそれ以上)いる場合にも当てはまります。」
- ^ラインフェルド、フレッド(1959). 『チェス完全講座』ダブルデイ・アンド・カンパニー社330ページ. ISBN 0385004648。
{{cite book}}:ISBN / 日付の非互換性(ヘルプ) - ^ a b Fine 1979、3ページ。
- ^ a bミュラー & ランプレヒト 2001、p. 17
- ^ a bスピルマン、ティスダル、ウェイド 1993、p. 7
- ^セイラワン 2003、5~7ページ
- ^シルマン 2007、191ページ
- ^ミュラー & ランプレヒト 2001、p. 18
- ^クルツドルファー 2003、155ページ
- ^ミュラー & ランプレヒト 2001、p. 19
- ^ハウエル 1997、138ページ
- ^シルマン 2007、33、188ページ
- ^ロイクロフト 1972年、246ページ
- ^バージェス 2009、16ページ
- ^フーパー&ワイルド 1992年、358~359ページ
- ^フーパー&ワイルド 1992、143ページ
- ^ “ティマン vs. ショート、ティルブルフ 1990” .チェスゲーム.com。
- ^フーパー&ワイルド 1992、376ページ
- ^エムズ 2004、122ページ
- ^ “ノゲイラス対ゴンゴラ、ラス・トゥーナス 2001” .チェスゲーム.com。 2005 年 2 月 8 日。2012 年 6 月 18 日に取得。
- ^スネイプ 2003、55ページ
- ^パンドルフィニ 2009、63ページ
- ^ジャスト&バーグ 2003、49、291ページ
- ^スピールマン、ティスダル、ウェイド、1993 年、p. 11
- ^ a bパンドルフィニ 2009、59ページ
- ^ファイン 1941、5~6ページ
参考文献
- バージェス、グラハム、ナン、ジョン、エムズ、ジョン(2004年)、世界最高のチェスゲームのマンモスブック(第2版)、キャロル&グラフ、ISBN 978-0-7867-1411-7
- バージェス、グラハム(2009年)、マンモス・ブック・オブ・チェス(第3版)、ランニング・プレス、ISBN 978-0-7624-3726-9
- デイヴィッドソン、ヘンリー(1949年)『チェス小史』マッケイ、ISBN 0-679-14550-8
{{citation}}:ISBN / 日付の非互換性(ヘルプ)(1981年ペーパーバック) - エムズ、ジョン(2004)、Starting Out:Minor Piece Endgames、Everyman Chess、ISBN 1-85744-359-4
- ファイン、ルーベン(1941年)、ベーシックチェスエンディングス、マッケイ、ISBN 0-679-14002-6
{{citation}}:ISBN / 日付の非互換性(ヘルプ) - ファイン、ルーベン(1979年)[初版1941年] 『チェスの基本的なエンディング』デイビッド・マッケイ社ISBN 0-679-14002-6。
- ファイン、ルーベン;ベンコ、パル(2003)『Basic Chess Endings』、マッケイ、ISBN 0-8129-3493-8
- ゴロンベック、ハリー(1976年)、チェスの歴史、パトナム、ISBN 0-399-11575-7
- フーパー、デイビッド、ワイルド、ケネス(1992年)、オックスフォード・コンパニオン・トゥ・チェス(第2版)、オックスフォード大学出版局、ISBN 0-19-280049-3
- ハウエル、ジェームズ(1997)、エッセンシャルチェスエンディング:トーナメントプレーヤーガイド、バッツフォード、ISBN 0-7134-8189-7
- ジャスト、ティム; バーグ、ダニエル B. (2003)、米国チェス連盟公式チェスルール(第5版)、マッケイ、ISBN 0-8129-3559-4
- クルツドルファー、ピーター(2003)、『チェスの基礎知識』アダムズメディア、ISBN 978-1-58062-586-9
- レヴィ、デイビッド、ニューボーン、モンティ(1991年)、コンピュータのチェスの遊び方、コンピュータサイエンスプレス、ISBN 0-7167-8121-2
- マッキーン、エリン(2005年)、新オックスフォード米語辞典(第2版)、オックスフォード大学出版局、ISBN 978-0-19-517077-1
- ミュラー, カルステン;フランク・ランプレヒト(2001)、『Fundamental Chess Endings』、Gambit Publications、ISBN 1-901983-53-6
- マレー、HJR(2012)[1913]、チェスの歴史、スカイホース、ISBN 978-1-62087-062-4
- パンドルフィーニ、ブルース(1988)、パンドルフィーニのエンドゲーム コース、ファイアサイド、サイモン & シュスター、ISBN 978-0-671-65688-1
- パンドルフィーニ、ブルース(2009)、エンドゲームワークショップ:実践的プレイヤーのための原則、ラッセルエンタープライズ、ISBN 978-1-888690-53-8
- ロイクロフト、ジョン(1972)、テストチューブチェス、ロンドン:フェイバー&フェイバー、ISBN 0-571-09573-9
- シラー、エリック(1999)、チェスの知恵百科事典(第1版)、Cardoza Publishing、ISBN 0-940685-93-0
- Seirawan, Yasser (2003) 『Winning Chess Endings』Everyman Chess、ISBN 1-85744-348-9
- シルマン、ジェレミー(2007年)、シルマンの完全エンドゲームコース:初心者からマスターまで、サイレスプレス、ISBN 978-1-890085-10-0
- スネイプ、イアン(2003)、チェスの終盤をシンプルに:自信を持って終盤にアプローチする方法、ガンビット出版、ISBN 1-901983-97-8
- スピルマン、ジョン;ティスダル、ジョン;ウェイド、ボブ(1993)「Batsford Chess Endings」、BT Batsford、ISBN 0-7134-4420-7
- サンナックス、アン(1970年)『チェス百科事典』セント・マーチンズ・プレス、ISBN 978-0-7091-4697-1