2次元フィルタ

2次元フィルタは、その重要性と様々な分野における高い適用性から、多大な開発努力が払われてきました。2次元の場合、多次元多項式は一般に因数分解できないため、1次元の場合とは状況が大きく異なります。つまり、任意の伝達関数を特定の実装に必要な形式に加工することは一般的に不可能です。2次元IIRフィルタの入出力関係は、定数係数の線形偏差分方程式に従います。この方程式から、入力サンプルと以前に計算された出力サンプルを用いて、出力サンプルの値を計算できます。出力サンプルの値はフィードバックされるため、2次元フィルタは1次元フィルタと同様に不安定になる可能性があります。

動機と応用

情報科学とコンピューティング技術の急速な発展により、デジタルフィルタの設計と応用の理論は飛躍的な発展を遂げました。私たちは実生活で、放送信号、テレビ信号、レーダー信号、携帯電話信号、ナビゲーション信号、電波天文信号、生物医学信号、制御信号、気象信号、地震信号、機械振動信号、リモートセンシングおよびテレメトリ信号など、さまざまな信号を目にします。これらの信号のほとんどはアナログ信号であり、デジタル信号はごく一部です。アナログ信号は、1次元、2次元、または多次元の独立変数の連続関数です。ほとんどの場合、1次元アナログ信号の変数は時間です。時間サンプリングと振幅の離散化の後、このようなアナログ信号は1次元デジタル信号になります。結果として得られるデジタル信号は、離散的なシーケンスで表すことができます。たとえば、一般的な信号の1つは音声信号です。2次元信号の例は画像です。フィルタは、信号を別の信号に変換できるシステムです。このような変換の例としては、ノイズ除去のための信号の平滑化、信号からの周波数成分の除去、信号強調のための周波数成分の増幅などが挙げられます。フィルタの設計と実装は、信号分析および処理技術における重要な分野です。フィルタは、信号の取得、伝送、処理、交換においても重要な役割を果たします。

問題の説明と基本概念

デジタルフィルタ

デジタル信号フィルタリングは、デジタルフィルタを実装することです。デジタルフィルタは、サンプリングされた離散時間信号に対して数学的演算を実行し、その信号の特定の側面を低減または強調するシステムです。入力信号と出力信号はすべてデジタル信号です。これは、連続時間アナログ信号で動作する電子回路である、もう 1 つの主要なタイプの電子フィルタであるアナログフィルタとは対照的です。実際、デジタルフィルタとアナログフィルタの基本的な概念は同じです。唯一の違いは、信号の種類とフィルタリングの方法です。デジタルフィルタは、ソフトウェアで数値的に実装でき、処理精度が高く、システムが安定しており、体積が小さく軽量であるなどの利点があります。デジタルフィルタにはインピーダンス整合がなく、デジタルフィルタは、アナログフィルタでは実現できない特殊なフィルタリング機能を実現できます。アナログ信号は、アナログ/デジタルコンバーターを使用してデジタルフィルタで処理することもできます。

2次元デジタルフィルタ

2次元フィルタは、2次元デジタル信号を処理するために使用されます。1次元と2次元のデジタルフィルタ問題の設計には重要な違いがあります。1次元の場合、フィルタの設計と実装はより簡単に別々に考えることができます。最初にフィルタを設計し、次に伝達関数を適切に操作することで、特定のネットワーク構造に必要な係数を決定できます。一方、2次元の場合、設計と実装はより密接に関連しています。一般に、多次元多項式は因数分解できないためです。つまり、任意の多次元伝達関数を、特定の実装に必要な形式に操作することは一般にできません。実装で因数分解可能な伝達関数しか実現できない場合、設計アルゴリズムはこのクラスのフィルタのみを設計するように調整する必要があります。これにより、設計問題が複雑になり、実用的な実装の数も制限されます。デジタルフィルタは、有限インパルス応答（FIR）と無限インパルス応答（IIR）の2つの主要なタイプに分類できます。 2次元FIRデジタルフィルタは非再帰アルゴリズム構造によって実現され、2次元IIRデジタルフィルタは再帰フィードバックアルゴリズム構造によって実現されます。^[1]

既存のアプローチ

2次元IIRフィルタの直接実装

IIRフィルタは、差分方程式を変形して、1つの出力サンプルを入力サンプルと以前に計算された出力サンプルで表すことで直接的に実装できます。^[2]第1象限フィルタの場合、入力信号と出力信号は次のように関係付けられます 。${\displaystyle x\left(n_{1},n_{2}\right)}$ ${\displaystyle y\left(n_{1},n_{2}\right)}$

${\displaystyle y\left(n_{1},n_{2}\right)=\sum _{l_{1}=0}^{L_{1}-1}\sum _{l_{2}=0}^{L_{2}-1}a(l_{1},l_{2})x(n_{1}-l_{1},n_{2}-l_{2})-\sum _{k_{1}=0}^{K_{1}-1}\sum _{k_{2}=0}^{K_{2}-1}b(k_{1},k_{2})y(n_{1}-k_{1},n_{2}-k_{2})}$

フィルタのインパルスに対する応答は定義によりインパルス応答なので、次の関係式を導くことができる。 ${\displaystyle \delta (n_{1},n_{2})}$ ${\displaystyle h\left(n_{1},n_{2}\right)}$

${\displaystyle h\left(n_{1},n_{2}\right)=a(l_{1},l_{2})-\sum _{k_{1}=0}^{K_{1}-1}\sum _{k_{2}=0}^{K_{2}-1}b(k_{1},k_{2})h(n_{1}-k_{1},n_{2}-k_{2})}$

両辺の2次元Z変換をとることで、システム関数を解くことができ、それは次のように与えられる。 ${\displaystyle H\left(z_{1},z_{2}\right)}$

${\displaystyle H_{z}(z_{1},z_{2})={\frac {\sum _{l_{1}=0}^{L_{1}-1}\sum _{l_{2}=0}^{L_{2}-1}a(l_{1},l_{2})z_{1}^{-l_{1}}z_{2}^{-l_{2}}}{\sum _{k_{1}=0}^{K_{1}-1}\sum _{k_{2}=0}^{K_{2}-1}b(k_{1},k_{2})z_{1}^{-k_{1}}z_{2}^{-k_{2}}}}={\frac {A_{z}(z_{1},z_{2})}{B_{z}(z_{1},z_{2})}}}$

この比率は、下の図に示すように、システム関数が に等しいFIRフィルタとシステム関数が に等しいIIRフィルタの2つのフィルタのカスケード接続の結果であると考えることができる。 ^[3]${\displaystyle A(z_{1},z_{2})}$ ${\displaystyle 1/B(z_{1},z_{2})}$

システム関数を用いたフィルタの表現。[3]より改変。${\displaystyle H(z_{1},z_{2})}$

2次元IIRフィルタの並列実装

複雑な2次元IIRフィルタを構築するもう一つの方法は、サブフィルタを並列接続することです。この場合、全体の伝達関数は次のようになります。

${\displaystyle H_{z}^{p}(z_{1},z_{2})=\sum _{i=1}^{N}H_{z}^{(i)}(z_{1},z_{2})}$

方程式を使用する

${\displaystyle H_{z}^{(i)}(z_{1},z_{2})={\frac {A_{z}^{(i)}(z_{1},z_{2})}{B_{z}^{(i)}(z_{1},z_{2})}}}$

そして、その合計を伝達関数の共通分母に当てはめると、展開された形が得られる。

${\displaystyle H_{z}^{p}(z_{1},z_{2})={\frac {A_{z}^{p}(z_{1},z_{2})}{B_{z}^{p}(z_{1},z_{2})}}={\frac {\sum _{j=1}^{N}\prod _{i\neq j}A_{z}^{(j)}(z_{1},z_{2})B_{z}^{(i)}(z_{1},z_{2})}{\prod _{i=1}^{N}B_{z}^{(i)}(z_{1},z_{2})}}}$

並列形式は、任意の2次元有理系関数を実装するためには使用できない。^[4]しかしながら、並列アーキテクチャによって実装可能な興味深い2次元IIRフィルタを合成することは可能である。例えば、複数の通過帯域を持つフィルタを設計する場合、並列形式は有利となる可能性がある。また、並列実装は、対称フィルタのように、インパルス応答が単一の象限に限定されない2次元IIRフィルタを実装する場合にも有用である。

N個の単純な2次元IIRフィルタを並列に接続して新しい2次元IIRフィルタを形成する。[3]より改変。

遺伝的アルゴリズムを用いた2次元IIRフィルタの設計

2次元IIRデジタルフィルタの設計手法は、文献で数多く報告されている。^{[1] [2] [3] [4]} 2013年には、遺伝的アルゴリズムが約10年にわたってデジタルフィルタの設計に成功裏に使用されていた。^{[引用が必要]}ここでは、GAベースの設計法と呼ばれる2次元IIRフィルタの設計方法を紹介する。

初期化

下の図は、提案されているGAベースの設計フローを示しています。フィルタ係数はCSD数値表現でエンコードされています。集団の初期化では、染色体がランダムに生成されます。各係数には、事前に指定された語長と非ゼロ桁の最大数があり、これらは任意の値に設定できます。^[5]

GAベースの設計フローチャート。[5]より改変。

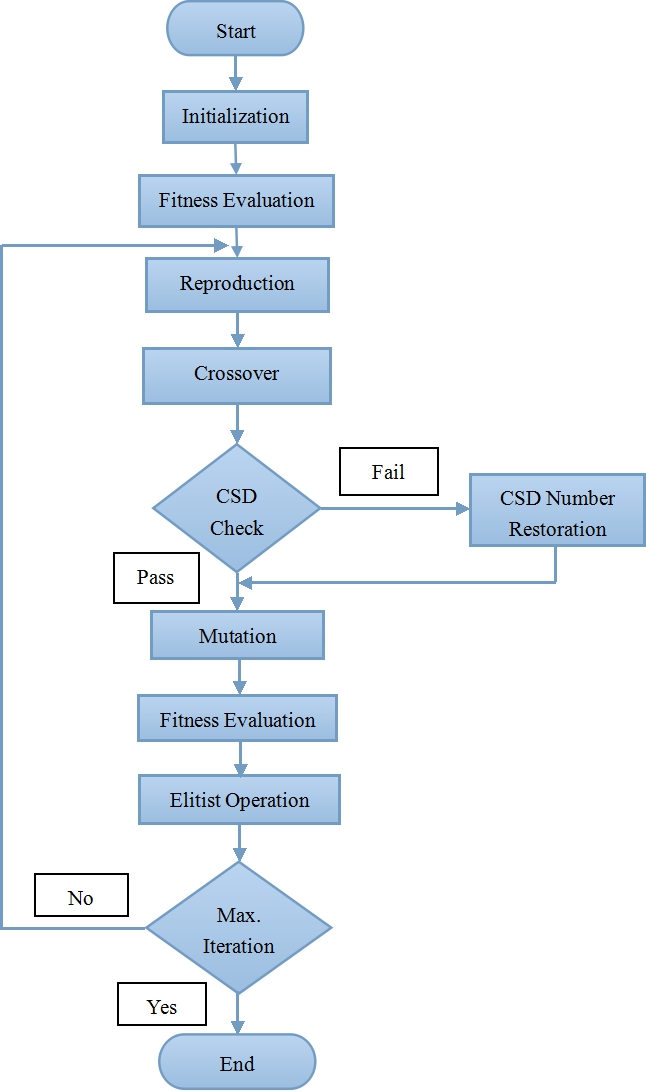
遺伝的オペレーター

ルーレットホイール選択は再生演算子として使用されます。各交叉操作の後、交叉点が位置する係数がCSD形式でチェックされます。突然変異操作は単純な1ビット反転です。突然変異後、子孫の各係数がCSD形式でチェックされます。

適応度評価と代替戦略

適応度評価は2段階のプロセスである。第1段階は、安定性三角形を用いて各2次セクションの安定性をチェックすることである。チェックに失敗した染色体には適応度値0が割り当てられる。古い世代の置き換えにはエリート戦略が適用される。繁殖後、子孫における最良の染色体と最悪の染色体が特定される。設計されたフィルタは、分子が非分離で分母が分離可能な伝達関数を持つ。^[6]フィルタ係数が事前に指定されたCSD形式で表現されるように、数値復元技術が使用される。

参考文献

1. TS Huang、「2次元再帰フィルタの安定性」、IEEE Transactions on Audio and Electroacoustics、vol. 20、no. 2、pp. 158–163、1972。
2. JS Lim、「2次元信号および画像処理」、Prentice-Hall International、1990年。
3. Dan E. Dudgeon、Russell M. Mersereau、「多次元デジタル信号処理」、Prentice-Hall信号処理シリーズ、ISBN 0136049591、1983年。
4. M. Ahmadi、「2次元再帰デジタルフィルタの設計」、Control and Dynamics System、vol. 78、pp. 131-181、1996年。
5. Li Liang、Majid Ahmadi、Maher Sid-Ahmed、「遺伝的アルゴリズムを使用した標準符号付き数字係数による 2D IIR フィルターの設計」、カナダ、ウィンザー大学、電気・コンピューター工学部。
6. A. Mazinani、M. Ahmadi、M. Shridhar、RS Lashkari、「2次元再帰デジタルフィルタの設計に対する斬新なアプローチ」、Journal of the Franklin Institute、Pergamon Press Ltd、vol. 329、no. 1、pp. 127-133、1992年。