メビウス変換

幾何学と複素解析において、複素平面のメビウス変換は、 1 つの複素変数z の形の 有理関数です。ここで、係数a、b、c、dは、 ad − bc ≠ 0を満たす複素数です。 $${\displaystyle f(z)={\frac {az+b}{cz+d}}}$$

幾何学的には、メビウス変換は、まず平面から単位球への逆立体射影を適用し、球を空間内の新しい位置と方向に移動および回転させ、次に立体射影を適用して球から平面にマッピングすることによって得られます。^{[ 1 ]}これらの変換は角度を保存し、すべての直線を直線または円にマッピングし、すべての円を直線または円にマッピングします。

メビウス変換は、複素射影直線の射影変換である。メビウス変換は、射影線型群PGL(2, C )であるメビウス群と呼ばれる群を形成する。メビウス変換は、その部分群とともに、数学および物理学において数多くの応用を持つ。

メビウス幾何学とその変換は、このケースを他のフィールド上の任意の数の次元に一般化します。

メビウス変換はアウグスト・フェルディナント・メビウスにちなんで名付けられました。ホモグラフィ、線型分数変換、双線型変換、スピン変換（相対性理論）の例です。 ^{[ 2 ]}

概要

メビウス変換は、拡張された複素平面 （つまり、無限遠点によって拡張された複素平面）上で定義されます。 ${\displaystyle {\widehat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}}$

立体射影は球面 と同一視され、リーマン球面と呼ばれる。あるいは、複素射影直線と考えることもできる。メビウス変換は、リーマン球面からそれ自身への全単射な等角写像、すなわち、複素多様体としてのリーマン球面 の自己同型である。あるいは、代数多様体としての の自己同型である。したがって、すべてのメビウス変換の集合は、合成によって群を形成する。この群はメビウス群と呼ばれ、 と表記されることもある。 ${\displaystyle {\widehat {\mathbb {C} }}}$ ${\displaystyle {\widehat {\mathbb {C} }}}$ ${\displaystyle \mathbb {C} \mathbb {P} ^{1}}$ ${\displaystyle \mathbb {C} \mathbb {P} ^{1}}$ ${\displaystyle \operatorname {Aut} ({\widehat {\mathbb {C} }})}$

メビウス群は、双曲 3 次元空間の方向保存等長変換群と同型であるため、双曲 3 次元多様体を研究する際に重要な役割を果たします。

物理学において、ローレンツ群の恒等成分は、メビウス群がリーマン球面に作用するのと同様に天球面に作用します。実際、これら2つの群は同型です。相対論的速度まで加速する観測者は、地球近傍で見られる星座のパターンが、微小なメビウス変換に従って連続的に変化するのを観測します。この観察は、しばしばツイスター理論の出発点とされています。

メビウス群の特定の部分群は、他の単連結リーマン面（複素平面および双曲平面）の自己同型群を形成する。そのため、メビウス変換はリーマン面の理論において重要な役割を果たす。すべてのリーマン面の基本群は、メビウス群の離散部分群である（フックス群およびクライン群を参照）。メビウス群の特に重要な離散部分群はモジュラー群であり、多くのフラクタル、モジュラー形式、楕円曲線、およびペル方程式の理論において中心的な役割を果たしている。

メビウス変換は、より一般的には、 n > 2次元空間において、n球面からn球面への全単射な共形写像として定義される。このような変換は、領域における共形写像の最も一般的な形である。リウヴィルの定理によれば、メビウス変換は、並進、相似、直交変換、反転の組み合わせとして表現できる。

意味

メビウス変換の一般的な形は次のように与えられます。 ここで、 a、b、c、dはad − bc ≠ 0を満たす任意の複素数です。 $${\displaystyle f(z)={\frac {az+b}{cz+d}},}$$

c ≠ 0の場合、この定義は リーマン球面全体に拡張され、$${\displaystyle {\begin{aligned}f\left({\frac {-d}{c}}\right)&=\infty ,\\f(\infty )&={\frac {a}{c}}.\end{aligned}}}$$

c = 0の場合、次のように定義する。 $${\displaystyle f(\infty )=\infty .}$$

したがって、メビウス変換は常にリーマン球面からリーマン球面への 全単射の正則関数です。

すべてのメビウス変換の成す集合は、合成のもとで群を形成する。この群は、合成と反転が正則写像となるような複素多様体構造を持つことができる。したがって、メビウス群は複素リー群となる。メビウス群は通常、リーマン球面の 自己同型群として表記される。${\displaystyle \operatorname {Aut} ({\widehat {\mathbb {C} }})}$

ad = bcの場合、上で定義した有理関数は定数となる（ただしc = d = 0 の場合は未定義となる）。 ただし、分母がゼロの分数は無視される。定数関数は全単射ではないため、メビウス変換とはみなされない。 $${\displaystyle {\frac {az+b}{cz+d}}={\frac {a}{c}}={\frac {b}{d}},}$$

代替の定義は、シュワルツ微分核として与えられます。

固定点

非恒等メビウス変換はいずれもリーマン球面上に2つの不動点 を持つ。ここでは不動点は重複度で数えられる。${\displaystyle \gamma _{1},\gamma _{2}}$ 放物型変換は、固定点が一致する変換です。これらの固定点の一方または両方が無限遠点となる場合があります。

固定点の決定

変換の不動点は 、不動点方程式f ( γ ) = γを解くことによって得られます。c ≠ 0の場合、この方程式を に展開し、二次方程式の公式 を適用することで、 2つの根が得られます 。根は 判別式 を持ち、 行列は 変換を表します。放物型変換は、判別式がゼロであるため、一致する不動点を持ちます。c がゼロでなく、判別式がゼロでない場合、変換は楕円型または双曲型になります。 $${\displaystyle f(z)={\frac {az+b}{cz+d}}}$$ $${\displaystyle c\gamma ^{2}-(ad)\gamma -b=0\ ,}$$ $${\displaystyle \gamma _{1,2}={\frac {(ad)\pm {\sqrt {(ad)^{2}+4bc}}}{2c}}={\frac {(ad)\pm {\sqrt {\Delta }}}{2c}}}$$ $${\displaystyle \Delta =(\operatorname {tr} {\mathfrak {H}})^{2}-4\det {\mathfrak {H}}=(a+d)^{2}-4(ad-bc),}$$ $${\displaystyle {\mathfrak {H}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}}$$

c = 0 のとき、二次方程式は線形方程式に退化し、変換は線形となる。これは、不動点の1つが無限遠点である状況に対応する。a ≠ d のとき、2つ目の不動点は有限であり、次のように与えられる 。$${\displaystyle \gamma =-{\frac {b}{ad}}.}$$

この場合、変換は平行移動、回転、拡大で構成される単純な変換になります。 $${\displaystyle z\mapsto \alpha z+\beta .}$$

c = 0かつa = dの場合、両方の固定点は無限大にあり、メビウス変換は純粋な変換に対応します。 $${\displaystyle z\mapsto z+\beta .}$$

位相的証明

位相的に、（非恒等）メビウス変換が2点（重複度付き）を固定するという事実は、球面の オイラー標数が2であることに対応する。$${\displaystyle \chi ({\hat {\mathbb {C} }})=2.}$$

まず、射影線型群PGL(2, K )は鋭く 3-推移的である 。つまり、異なる点からなる任意の二つの順序付き三重写像に対して、メビウス変換と同様に、一方の三重写像をもう一方の三重写像へ写す唯一の写像が存在する。これは、群が3次元であるため、基本的に次元を数えるという代数的証明によって証明される。したがって、少なくとも3点を固定する写像は恒等写像となる。

次に、メビウス群を と同一視することにより、任意のメビウス関数が恒等写像にホモトピーであることがわかります。実際、一般線型群の任意の元はガウス・ジョルダン消去法によって恒等写像に還元できます。これは、射影線型群もパス連結であることを示しており、恒等写像にホモトピーを与えます。レフシェッツ・ホップの定理は、有限個の固定点を持つ写像の固定点の添え字（この文脈では重複度）の和が、写像のレフシェッツ数に等しいことを述べています。この場合、レフシェッツ数はホモロジー群上の恒等写像の軌跡、つまり単にオイラー標数です。 ${\displaystyle \mathrm {PGL} (2,\mathbb {C} )}$

対照的に、実射影直線の射影線型群PGL(2, R )は、点を固定する必要がない。例えば、（実）固定点を持たない。複素変換として± i ^{[注 1 ]}を固定する のに対し、写像2 x は0と∞の2点を固定する。これは、円（実射影直線）のオイラー標数が0であるという事実に対応しており、したがって、レフシェッツの不動点定理は、少なくとも0点を固定する必要があるが、それ以上の点を固定してもよいと述べているに過ぎない。 ${\displaystyle (1+x)/(1-x)}$

正規形

メビウス変換は、いわゆる正規形と呼ばれる不動点を用いて記述されることもあります。まず、2つの異なる不動点が存在する非放物型の場合を扱います。

非放物線の場合:

非放物型変換はすべて、拡大／回転、すなわち 0 と ∞ を固定点とする ( k ∈ C )の形の変換と共役である。これを理解するには 、点 ( γ ₁ , γ _{2 ) を (0, ∞ ) に写像する。ここで、} γ ₁とγ ₂は互いに異なり有限であると仮定する。もしどちらか一方が既に無限遠にある場合、g を修正して無限遠を固定し、もう一方の点を 0 に写像することができる。 $${\displaystyle z\mapsto kz}$$ $${\displaystyle g(z)={\frac {z-\gamma _{1}}{z-\gamma _{2}}}}$$

f が異なる不動点 ( γ ₁ , γ ₂ ) を持つ場合、変換は0 と ∞ に不動点を持ち、したがって拡大変換となる。変換fの不動点方程式は次のように書ける 。${\displaystyle gfg^{-1}}$ ${\displaystyle gfg^{-1}(z)=kz}$ $${\displaystyle {\frac {f(z)-\gamma _{1}}{f(z)-\gamma _{2}}}=k{\frac {z-\gamma _{1}}{z-\gamma _{2}}}.}$$

fについて解くと次のようになります (行列形式)。 または、固定点の 1 つが無限大にある場合は次のようになります。 $${\displaystyle {\mathfrak {H}}(k;\gamma _{1},\gamma _{2})={\begin{pmatrix}\gamma _{1}-k\gamma _{2}&(k-1)\gamma _{1}\gamma _{2}\\1-k&k\gamma _{1}-\gamma _{2}\end{pmatrix}}}$$ $${\displaystyle {\mathfrak {H}}(k;\gamma ,\infty )={\begin{pmatrix}k&(1-k)\gamma \\0&1\end{pmatrix}}.}$$

上記の式から、固定点における fの導関数を計算することができる。$${\displaystyle f'(\gamma _{1})=k}$$ $${\displaystyle f'(\gamma _{2})=1/k.}$$

不動点の順序が与えられれば、fの乗数 ( k ) の1つをfの特性定数として区別できることに注目してください。不動点の順序を逆にすることは、特性定数の逆乗数を取ることと等価です。 $${\displaystyle {\mathfrak {H}}(k;\gamma _{1},\gamma _{2})={\mathfrak {H}}(1/k;\gamma _{2},\gamma _{1}).}$$

斜航変換において、| k | > 1の場合には、 γ ₁が反発固定点、γ ₂が引力固定点と呼ばれます。| k | < 1の場合には、役割が逆になります。

放物線の場合:

放物線の場合、固定点γは1つだけです。この点を無限大へ送る変換は、 γが既に無限大にある 場合は恒等変換です。この変換は無限大を固定するため、平行移動となります。 $${\displaystyle g(z)={\frac {1}{z-\gamma }}}$$ ${\displaystyle gfg^{-1}}$ $${\displaystyle gfg^{-1}(z)=z+\beta \,.}$$

ここで、βは並進長と呼ばれる。放物線変換の固定点公式は次のようになる。 $${\displaystyle {\frac {1}{f(z)-\gamma }}={\frac {1}{z-\gamma }}+\beta .}$$

fを（行列形式で） 解くと次のように なる。$${\displaystyle {\mathfrak {H}}(\beta ;\gamma )={\begin{pmatrix}1+\gamma \beta &-\beta \gamma ^{2}\\\beta &1-\gamma \beta \end{pmatrix}}}$$ ${\displaystyle \det {\mathfrak {H}}(\beta ;\gamma )=|{\mathfrak {H}}(\beta ;\gamma )|=\det {\begin{pmatrix}1+\gamma \beta &-\beta \gamma ^{2}\\\beta &1-\gamma \beta \end{pmatrix}}=1-\gamma ^{2}\beta ^{2}+\gamma ^{2}\beta ^{2}=1}$

γ = ∞の場合: $${\displaystyle {\mathfrak {H}}(\beta ;\infty )={\begin{pmatrix}1&\beta \\0&1\end{pmatrix}}}$$

βはfの特性定数ではないことに注意してください。f は放物線変換では常に 1 です。上記の式から、以下の式を計算できます。 $${\displaystyle f'(\gamma )=1.}$$

変革の極

この点はの極と呼ばれます。これは⁠ ⁠の下で無限遠点に変換される点です。 ${\textstyle z_{\infty }=-{\frac {d}{c}}}$ ${\displaystyle {\mathfrak {H}}}$ ${\displaystyle {\mathfrak {H}}}$

逆極とは、無限遠点が変換された点です。2つの極の中点は、常に2つの固定点の中点と同じです。 ${\textstyle Z_{\infty }={\frac {a}{c}}}$ $${\displaystyle \gamma _{1}+\gamma _{2}=z_{\infty }+Z_{\infty }.}$$

これら 4 つの点は、変換の 特性平行四辺形と呼ばれることもある平行四辺形の頂点です。

変換は、 2つの固定点γ ₁、γ ₂および極で指定できます。 ${\displaystyle {\mathfrak {H}}}$ ${\displaystyle z_{\infty }}$

$${\displaystyle {\mathfrak {H}}={\begin{pmatrix}Z_{\infty }&-\gamma _{1}\gamma _{2}\\1&-z_{\infty }\end{pmatrix}},\;\;Z_{\infty }=\gamma _{1}+\gamma _{2}-z_{\infty }.}$$

これにより、 kと与えられたの間の変換式を導く​​ことができ、 これは次のように簡約される 。${\displaystyle z_{\infty }}$ ${\displaystyle \gamma _{1},\gamma _{2}}$ $${\displaystyle z_{\infty }={\frac {k\gamma _{1}-\gamma _{2}}{1-k}}}$$ $${\displaystyle k={\frac {\gamma _{2}-z_{\infty }}{\gamma _{1}-z_{\infty }}}={\frac {Z_{\infty }-\gamma _{1}}{Z_{\infty }-\gamma _{2}}}={\frac {a-c\gamma _{1}}{a-c\gamma _{2}}},}$$ $${\displaystyle k={\frac {(a+d)+{\sqrt {(a-d)^{2}+4bc}}}{(a+d)-{\sqrt {(a-d)^{2}+4bc}}}}.}$$

最後の式は、（互いに逆数の）固有値比の1つと一致する（前の節の変換の特性定数に関する議論と比較のこと）。その特性多項式は、 根を持つ ${\textstyle {\frac {\lambda _{1}}{\lambda _{2}}}}$ ${\displaystyle {\mathfrak {H}}}$ $${\displaystyle \det(\lambda I_{2}-{\mathfrak {H}})=\lambda ^{2}-\operatorname {tr} {\mathfrak {H}}\,\lambda +\det {\mathfrak {H}}=\lambda ^{2}-(a+d)\lambda +(ad-bc)}$$ $${\displaystyle \lambda _{i}={\frac {(a+d)\pm {\sqrt {(a-d)^{2}+4bc}}}{2}}={\frac {(a+d)\pm {\sqrt {(a+d)^{2}-4(ad-bc)}}}{2}}=c\gamma _{i}+d\,.}$$

単純なメビウス変換と合成

メビウス変換は、一連の単純な変換として 構成できます。

次の単純な変換もメビウス変換です。

• ${\displaystyle f(z)=z+b\quad (a=1,c=0,d=1)}$ 翻訳です。
• ${\displaystyle f(z)=az\quad (b=0,c=0,d=1)}$ は、相似性（均一なスケーリング）と回転の組み合わせです。 の場合は回転、 の場合は相似性です。${\displaystyle |a|=1}$ ${\displaystyle a\in \mathbb {R} }$
• ${\displaystyle f(z)=1/z\quad (a=0,b=1,c=1,d=0)}$ （実軸に対する反転と鏡映）

単純な変換の合成

の場合、次のようにします。 ${\displaystyle c\neq 0}$

• ${\displaystyle f_{1}(z)=z+d/c\quad }$ （翻訳：d / c）
• ${\displaystyle f_{2}(z)={\frac {1}{-z}}\quad }$ （実軸に対する反転と反射）
• ${\displaystyle f_{3}(z)={\frac {bc-ad}{c^{2}}}z\quad }$ （相似性と回転）
• ${\displaystyle f_{4}(z)=z+a/c\quad }$ （翻訳：a / c）

すると、これらの関数は 合成 することができ 、 つまり 、 $${\displaystyle f(z)={\frac {az+b}{cz+d}},}$$ $${\displaystyle f=f_{4}\circ f_{3}\circ f_{2}\circ f_{1}.}$$ $${\displaystyle {\frac {az+b}{cz+d}}={\frac {a}{c}}+{\frac {e}{z+{\frac {d}{c}}}},}$$ $${\displaystyle e={\frac {bc-ad}{c^{2}}}.}$$

この分解により、メビウス変換の多くの特性が明らかになります。

基本的な性質

メビウス変換は、より単純な変換の列と等価である。この合成により、メビウス変換の多くの性質が明らかになる。

逆変換の式

逆メビウス変換の存在とその明示的な式は、より単純な変換の逆関数の合成によって容易に導かれる。つまり、関数g ₁、g ₂、g ₃、g _{4を定義し、各}g _iがf _iの逆関数となるようにする。すると、この合成 によって逆関数の式が得られる。 $${\displaystyle g_{1}\circ g_{2}\circ g_{3}\circ g_{4}(z)=f^{-1}(z)={\frac {dz-b}{-cz+a}}}$$

角度の保存と一般化された円

この分解から、メビウス変換は円反転の非自明な性質をすべて引き継ぐことがわかります。例えば、角度の保存は、円反転が角度を保存することを証明することに帰着します。なぜなら、他の種類の変換は拡大変換と等長変換（並進、鏡映、回転）であり、これらは角度を自明に保存するからです。

さらに、メビウス変換は一般円を一般円に写像します。これは、円反転がこの性質を持つためです。一般円は円または直線のいずれかであり、後者は無限遠点を通る円とみなされます。メビウス変換は必ずしも円を円に、直線を直線に写像するわけではなく、両者を混在させることもできることに注意してください。円を別の円に写像する場合でも、必ずしも最初の円の中心を2番目の円の中心に写像するとは限りません。

クロス比保存

複比はメビウス変換に対して不変である。つまり、メビウス変換が4つの異なる点をそれぞれ4つの異なる点に写す場合、 ${\displaystyle z_{1},z_{2},z_{3},z_{4}}$ ${\displaystyle w_{1},w_{2},w_{3},w_{4}}$ $${\displaystyle {\frac {(z_{1}-z_{3})(z_{2}-z_{4})}{(z_{2}-z_{3})(z_{1}-z_{4})}}={\frac {(w_{1}-w_{3})(w_{2}-w_{4})}{(w_{2}-w_{3})(w_{1}-w_{4})}}.}$$

点の1つが無限遠点である場合、適切な極限をとることによって複比を定義する必要があります。例えば、複比は ${\displaystyle z_{1},z_{2},z_{3},z_{4}}$ ${\displaystyle z_{1},z_{2},z_{3},\infty }$ $${\displaystyle {\frac {(z_{1}-z_{3})}{(z_{2}-z_{3})}}.}$$

4つの異なる点の複比が実数となるのは、それらを通る直線または円が存在する場合に限られます。これは、メビウス変換が一般円を保存することを示す別の方法です。

活用

二点z ₁とz _{2 が一般円}Cに関して共役であるとは、z ₁とz ₂を通り、 C を二点aとbで切る一般円Dが与えられ、( z ₁ , z ₂ ; a , b )が調和複比（すなわち、それらの複比が -1）であるときである。この性質は円Dの選択に依存しない。この性質は、直線または円に関して対称であると言われることもある。 ^{[ 3 ] [ 4 ]}

2点z、z ^{∗ が}直線に関して共役であるとは、その直線に関して対称であることを意味する。2点が円に関して共役であるとは、その円に関して 反転によって交換されることを意味する。

点z ^{∗ は}、点z _{0における}e ^iθに基づくベクトルによって決まる直線Lのとき、 zと共役である。これは次のように明示的に表される。 $${\displaystyle z^{*}=e^{2i\theta }\,{\overline {z-z_{0}}}+z_{0}.}$$

点z ^{∗ は、} C がz ₀を中心とする半径rの円であるとき、zと共役である。これは次のように明示的に表される。 $${\displaystyle z^{*}={\frac {r^{2}}{\overline {z-z_{0}}}}+z_{0}.}$$

メビウス変換は一般化された円と複比を保存するので、共役も保存されます。

射影行列表現

メビウス群とPGL(2, C)の同型性

複素射影直線CP ¹へのPGL(2, C )の自然作用は、リーマン球面へのメビウス群の自然作用と全く同じである。

複素射影直線とリーマン球面の対応

ここで、射影直線CP ¹とリーマン球面は次のように同一視されます。 $${\displaystyle [z_{1}:z_{2}]\ \thicksim {\frac {z_{1}}{z_{2}}}.}$$

ここで [ z ₁ : z ₂ ] はCP ¹上の同次座標であり、点 [1:0] はリーマン球面の点∞に対応する。同次座標を用いることで、 ∞を扱う場合分けが不要になるため、メビウス変換を含む多くの計算を簡略化できる。

複素射影直線上のPGL(2, C)の作用

任意の可逆複素2×2行列は 射影直線上で 次 のように作用する。$${\displaystyle {\mathfrak {H}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}}$$ $${\displaystyle z=[z_{1}:z_{2}]\mapsto w=[w_{1}:w_{2}],}$$ $${\displaystyle {\begin{pmatrix}w_{1}\\w_{2}\end{pmatrix}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}{\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix}}={\begin{pmatrix}az_{1}+bz_{2}\\cz_{1}+dz_{2}\end{pmatrix}}.}$$

その結果は $${\displaystyle w=[w_{1}:w_{2}]=[az_{1}+bz_{2}:cz_{1}+dz_{2}]}$$

これは、上記の識別を用いると、リーマン球面上の次の点に対応する。

$${\displaystyle w=[az_{1}+bz_{2}:cz_{1}+dz_{2}]\thicksim {\frac {az_{1}+bz_{2}}{cz_{1}+dz_{2}}}={\frac {a{\frac {z_{1}}{z_{2}}}+b}{c{\frac {z_{1}}{z_{2}}}+d}}.}$$

リーマン球面上のメビウス変換との同値性

上の行列は、その行列式ad − bcがゼロでない場合に限り逆行列となるので、メビウス変換群の作用と複素射影直線上のPGL(2, C )の作用が同一視される。この同一視において、上の行列はメビウス変換に対応する。${\displaystyle {\mathfrak {H}}}$ ${\displaystyle z\mapsto {\frac {az+b}{cz+d}}.}$

この識別は群同型です。非ゼロのスカラーによるの乗算はPGL(2, C )の要素を変更せず、この乗算はすべての行列要素に を乗算することから構成されるため、対応するメビウス変換は変更されません。 ${\displaystyle {\mathfrak {H}}}$ ${\displaystyle \lambda }$ ${\displaystyle \lambda ,}$

その他のグループ

任意の体Kに対して、同様に射影線型自己同型群PGL(2, K )を分数線型変換群と同一視することができる。これは広く用いられており、例えば実数直線のホモグラフィの研究やその光学への応用などが挙げられる。

行列式の平方根で割ると、行列式1の行列が得られる。これにより、特殊線型群SL(2, C )からPGL(2, C )への射影群準同型が誘導され、その核はとなる。 ${\displaystyle {\mathfrak {H}}}$ ${\displaystyle \pm I}$

これにより、メビウス群が半単純かつ非コンパクトである3次元複素リー群（または6次元実リー群）であること、そして SL(2, C ) がPSL(2, C )の二重被覆であることを示すことができる。SL (2, C )は単連結であるため、メビウス群の普遍被覆であり、メビウス群の 基本群はZ ₂である。

3点による変換の指定

リーマン球面上の3つの異なる点の集合と、2つ目の異なる点の集合⁠ ⁠が与えられたとき、 ⁠ ⁠に対して となるメビウス変換が1つだけ存在します。（言い換えると、メビウス群のリーマン球面への作用は、鋭く3推移的です。）与えられた点の集合から決定する方法はいくつかあります。 ${\displaystyle z_{1},z_{2},z_{3}}$ ${\displaystyle w_{1},w_{2},w_{3}}$ ${\displaystyle f(z)}$ ${\displaystyle f(z_{j})=w_{j}}$ ${\displaystyle j=1,2,3}$ ${\displaystyle f(z)}$

まず0、1、∞にマッピングする

行列のメビウス 変換がそれぞれ⁠ ⁠に 写像されることは簡単に確認できます 。 のいずれかが である場合、 の適切な式は、まずすべての要素を ⁠ ⁠ で割り、次に極限⁠ ⁠を取ることで上記の式から得られます。 $${\displaystyle f_{1}(z)={\frac {(z-z_{1})(z_{2}-z_{3})}{(z-z_{3})(z_{2}-z_{1})}}}$$ $${\displaystyle {\mathfrak {H}}_{1}={\begin{pmatrix}z_{2}-z_{3}&-z_{1}(z_{2}-z_{3})\\z_{2}-z_{1}&-z_{3}(z_{2}-z_{1})\end{pmatrix}}}$$ ${\displaystyle z_{1},z_{2}{\text{ and }}z_{3}}$ ${\displaystyle 0,1,\ {\text{and}}\ \infty }$ ${\displaystyle z_{j}}$ ${\displaystyle \infty }$ ${\displaystyle {\mathfrak {H}}_{1}}$ ${\displaystyle z_{j}}$ ${\displaystyle z_{j}\to \infty }$

が同様に定義され、に写像される場合、に写像される 行列は${\displaystyle {\mathfrak {H}}_{2}}$ ${\displaystyle w_{1},w_{2},w_{3}}$ ${\displaystyle 0,1,\ {\text{and}}\ \infty ,}$ ${\displaystyle {\mathfrak {H}}}$ ${\displaystyle z_{1,2,3}}$ ${\displaystyle w_{1,2,3}}$ $${\displaystyle {\mathfrak {H}}={\mathfrak {H}}_{2}^{-1}{\mathfrak {H}}_{1}.}$$

（順序付けられていない集合としての）の安定化群は、非調和群として知られる部分群である。 ${\displaystyle \{0,1,\infty \}}$

明示的な行列式

この方程式は 、 -平面 における標準的な双曲線 の方程式と同等です。したがって、ある三つ組を別の三つ組にマッピングするメビウス変換を構築する問題は、点⁠ ⁠を通る双曲線の係数を見つけることと同等です。明示的な方程式は、最初の行に沿って ラプラス展開 によって行列式を評価することで見つけることができ、その結果、表現する行列⁠ ⁠の 係数に対する明示的な式が得られます。構築された行列の行列式は⁠ ⁠に等しく、それぞれが一組ずつ異なる場合はゼロにならないため、メビウス変換は明確に定義されます。点の1つまたはが⁠ ⁠である場合、まず4つの行列式すべてをこの変数で割り、次に変数が⁠ ⁠に近づくにつれて極限をとります。 $${\displaystyle w={\frac {az+b}{cz+d}}}$$ $${\displaystyle cwz-az+dw-b=0}$$ ${\displaystyle (z,w)}$ ${\displaystyle {\mathfrak {H}}(z)}$ ${\displaystyle (z_{1},z_{2},z_{3})}$ ${\displaystyle (w_{1},w_{2},w_{3})}$ ${\displaystyle a,b,c,d}$ ${\displaystyle (z_{i},w_{i})}$ $${\displaystyle {\begin{vmatrix}zw&z&w&1\\z_{1}w_{1}&z_{1}&w_{1}&1\\z_{2}w_{2}&z_{2}&w_{2}&1\\z_{3}w_{3}&z_{3}&w_{3}&1\end{vmatrix}}\,}$$ $${\displaystyle {\begin{aligned}a&=z_{1}w_{1}(w_{2}-w_{3})+z_{2}w_{2}(w_{3}-w_{1})+z_{3}w_{3}(w_{1}-w_{2}),\\[5mu]b&=z_{1}w_{1}(z_{2}w_{3}-z_{3}w_{2})+z_{2}w_{2}(z_{3}w_{1}-z_{1}w_{3})+z_{3}w_{3}(z_{1}w_{2}-z_{2}w_{1}),\\[5mu]c&=w_{1}(z_{3}-z_{2})+w_{2}(z_{1}-z_{3})+w_{3}(z_{2}-z_{1}),\\[5mu]d&=z_{1}w_{1}(z_{2}-z_{3})+z_{2}w_{2}(z_{3}-z_{1})+z_{3}w_{3}(z_{1}-z_{2})\end{aligned}}}$$ ${\displaystyle a,b,c,d}$ ${\displaystyle {\mathfrak {H}}}$ ${\displaystyle {\mathfrak {H}}}$ ${\displaystyle (z_{1}-z_{2})(z_{1}-z_{3})(z_{2}-z_{3})(w_{1}-w_{2})(w_{1}-w_{3})(w_{2}-w_{3})}$ ${\displaystyle z_{j}}$ ${\displaystyle w_{j}}$ ${\displaystyle z_{j}}$ ${\displaystyle w_{j}}$ ${\displaystyle \infty }$ ${\displaystyle \infty }$

メビウス群の部分群

メビウス変換の係数が⁠ ⁠の実数である必要がある場合、メビウス群の部分群はPSL(2, R )と表記されます。これは、上半平面H = { x + i y  : y > 0}をそれ自身に写すメビウス変換の群であり、すべての双正則（または同値：全単射、共形、方向保存）写像H → Hの群に等しくなります。適切な測定基準が導入されると、上半平面は双曲面H ²のモデル、ポアンカレ半平面モデルになり、PSL(2, R )はこのモデルにおける H ²のすべての方向保存等長変換の群です。${\displaystyle a,b,c,d}$ ${\displaystyle ad-bc=1}$

開円板D = { z  : | z | < 1}をそれ自身に 写すすべてのメビウス変換の部分群は、 ∈ R 、 b ∈ C 、 | b | < 1 を満たす形式のすべての変換から構成される。これは、すべての双正則写像（または同値：全単射、角度保存、方向保存） D → Dの群に等しい。適切な計量を導入することで、開円板は双曲面の別のモデルであるポアンカレ円板モデルに変換され、この群はこのモデルにおけるH ²のすべての方向保存等長写像の群となる。 $${\displaystyle f(z)=e^{i\phi }{\frac {z+b}{{\bar {b}}z+1}}}$$ ${\displaystyle \phi }$

上記の両方の部分群はH ²の等長群として働くので、同型である。具体的な同型は、 開単位円板を上半平面に全単射に写す 変換との 共役によって与えられる。$${\displaystyle f(z)={\frac {z+i}{iz+1}}}$$

あるいは、半径r、中心r iの開円板を考えます。この円板におけるポアンカレ円板モデルは、 r が∞に近づくにつれて上半平面モデルと同一になります。

メビウス群の最大コンパクト部分群は( Tóth 2002 ) ^{[ 5 ]}によって与えられ 、同型写像の下で射影特殊ユニタリ群PSU(2, C )に対応し、これは三次元回転の特殊直交群SO(3) と同型であり、リーマン球面の回転として解釈できる。すべての有限部分群はこの最大コンパクト群に共役であり、したがってこれらは三次元の多面体群、すなわち点群と正確に一致する。 ${\displaystyle {\mathcal {M}}}$ $${\displaystyle {\mathcal {M}}_{0}:=\left\{z\mapsto {\frac {uz-{\bar {v}}}{vz+{\bar {u}}}}:|u|^{2}+|v|^{2}=1\right\},}$$ ${\displaystyle {\mathcal {M}}\cong \operatorname {PSL} (2,\mathbb {C} )}$

メビウス変換の二十面体群は、フェリックス・クラインによって五次方程式の解析解を与えるために使われた（Klein 1913）。現代的な解説は（Tóth 2002）に示されている。^{[ 6 ]}

メビウス変換の係数a , b , c , dがad − bc = 1を満たす整数であるとすると、モジュラー群PSL(2, Z )が得られます。これはPSL(2, R )の離散部分群であり、複素平面上の格子、楕円関数、楕円曲線の研究で重要です。PSL (2, R )の離散部分群はフックス群として知られ、リーマン面の研究で重要です。

分類

双曲変換が示されている。単位円の原像は、距離比がc / aで焦点が − b / aと − d / cにあるアポロニウスの円である。

同じ焦点 − b / aと − d / cの場合、赤い円は原点を通る光線にマッピングされます。

以下の議論では、表現行列が⁠ ⁠となるように正規化されていると常に仮定します。 ${\displaystyle {\mathfrak {H}}}$ ${\displaystyle \det {\mathfrak {H}}=ad-bc=1}$

非恒等メビウス変換は、一般的に放物型、楕円型、双曲型、斜航型（ロクソドロミック）の4種類に分類され、双曲型は斜航型の一部です。この分類は代数的にも幾何学的にも重要な意味を持ちます。幾何学的には、以下の図に示すように、種類によって複素平面の変換が異なります。

4つのタイプは、トレース を見ることで区別できます。トレースは共役に対して不変、つまり であり、 共役類のすべての要素は同じトレースを持ちます。すべてのメビウス変換は、その表現行列が行列式1を持つように書き表すことができます（要素に適切なスカラーを乗じることによって）。を持つ2つのメビウス変換（どちらも恒等変換と等しくない）が共役である場合、かつその場合のみ、${\displaystyle \operatorname {tr} {\mathfrak {H}}=a+d}$ $${\displaystyle \operatorname {tr} \,{\mathfrak {GHG}}^{-1}=\operatorname {tr} \,{\mathfrak {H}},}$$ ${\displaystyle {\mathfrak {H}}}$ ${\displaystyle {\mathfrak {H}},{\mathfrak {H}}'}$ ${\displaystyle \det {\mathfrak {H}}=\det {\mathfrak {H}}'=1}$ ${\displaystyle \operatorname {tr} ^{2}{\mathfrak {H}}=\operatorname {tr} ^{2}{\mathfrak {H}}'.}$

放物線変換

行列式が 1の行列で定義される非恒等メビウス変換は、の場合 、放物型であるという （したがって、トレースはプラスまたはマイナス 2 になる。は符号までしか決定されないため、特定の変換ではどちらでも起こり得る）。実際、 の選択肢の 1 つは、恒等行列と同じ特性多項式X ² − 2 X + 1を持つため、ユニポレント である。メビウス変換が放物型となるのは、拡張複素平面上にちょうど 1 つの固定点を持つ場合であり、これは、 が複素平面での変換を記述する共役行列 によって定義できる場合のみである 。 ${\displaystyle {\mathfrak {H}}}$ $${\displaystyle \operatorname {tr} ^{2}{\mathfrak {H}}=(a+d)^{2}=4}$$ ${\displaystyle {\mathfrak {H}}}$ ${\displaystyle {\mathfrak {H}}}$ ${\displaystyle {\widehat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}}$ $${\displaystyle {\begin{pmatrix}1&1\\0&1\end{pmatrix}}}$$

における与えられた不動点を持つすべての放物型メビウス変換の集合は、恒等変換とともに、行列群に同型な 部分群を形成します。これは、ボレル部分群の単能根基 の例です（メビウス群、または行列群の場合はSL(2, C )の例です。この概念は、任意の簡約リー群に対して定義されています）。 ${\displaystyle {\widehat {\mathbb {C} }}}$ $${\displaystyle \left\{{\begin{pmatrix}1&b\\0&1\end{pmatrix}}\mid b\in \mathbb {C} \right\};}$$

特性定数

すべての非放物型変換には 2 つの固定点があり、 の共役行列によって定義されます。この行列は、 λが 0、1、または -1 以外の 値を持ち、変換の特性定数または乗数と呼ばれる複素数k = λ ²の乗算による拡大/回転に対応します。 $${\displaystyle {\begin{pmatrix}\lambda &0\\0&\lambda ^{-1}\end{pmatrix}}}$$

楕円変換

スミスチャートは、電気技術者が伝送線路の解析に用いるもので、楕円メビウス変換Γ = ( z − 1)/( z + 1)を視覚的に表現したものです。スミスチャート上の各点は、|Γ|<1 において、 zの値（左下）とそれに対応する Γ の値（右下）を同時に表します。

変換は、行列式1の 行列で表すことができ、${\displaystyle {\mathfrak {H}}}$ $${\displaystyle 0\leq \operatorname {tr} ^{2}{\mathfrak {H}}<4.}$$

変換が楕円型となるのは、 | λ | = 1かつλ ≠ ±1 のときのみです。 と書くと、楕円型変換はα が実数 であるときと共役になります 。 ${\displaystyle \lambda =e^{i\alpha }}$ $${\displaystyle {\begin{pmatrix}\cos \alpha &-\sin \alpha \\\sin \alpha &\cos \alpha \end{pmatrix}}}$$

特性定数kを持つ任意 のに対して、 の特性定数はk ^{n で}ある。したがって、有限位数のメビウス変換はすべて楕円型変換であり、すなわちλが1 の根、あるいは同値としてαがπの有理倍であるような変換である。分数倍の最も単純な可能性はα = π /2であり、これは の唯一の場合でもあり、 とも表記される。${\displaystyle {\mathfrak {H}}}$ ${\displaystyle {\mathfrak {H}}^{n}}$ ${\displaystyle \operatorname {tr} {\mathfrak {H}}=0}$ 円変換。これは幾何学的には、2つの固定点の周りの180°回転に相当します。このクラスは、行列形式で次のように表されます。 {0, 1, ∞}を固定する3つの代表があり、これらはこれらの3点の対称群における3つの転置です。これは1を固定し、0を∞（点1と-1の周りの180°回転）、これ∞を∞の周りの180°回転）、これは0を固定し、1を∞（点0と2の周りの180°回転）。 $${\displaystyle {\begin{pmatrix}0&-1\\1&0\end{pmatrix}}.}$$ ${\displaystyle 1/z,}$ ${\displaystyle 1-z}$ ${\displaystyle z/(z-1)}$

双曲変換

変換が双曲型であるとは、そのトレースが実数で ある行列で表現できる場合である。${\displaystyle {\mathfrak {H}}}$ $${\displaystyle \operatorname {tr} ^{2}{\mathfrak {H}}>4.}$$

変換は、 λが実数でλ ≠ ±1の場合にのみ双曲型になります。

斜航変換

が[0, 4]に含まれない場合、変換は斜航的であると言われる。変換が斜航的であるための必要条件は、 の場合のみである。 ${\displaystyle \operatorname {tr} ^{2}{\mathfrak {H}}}$ ${\displaystyle |\lambda |\neq 1}$

歴史的に、航程線（ロクソドローム）または等角航路による航行は、一定の方位を持つ経路を指します。結果として得られる経路は対数螺旋であり、これは、ロクソドロミック・メビウス変換が複素平面に対して行う変換に似た形状です。以下の幾何学的図形を参照してください。

一般分類

変換	トレースの二乗	乗数	クラス代表
円形	σ = 0	k = −1	${\displaystyle {\begin{pmatrix}i&0\\0&-i\end{pmatrix}}}$	z ↦ − z
楕円形	0 ≤ σ < 4 ${\displaystyle \sigma =2+2\cos(\theta )}$	| k | = 1 ${\displaystyle k=e^{\pm i\theta }\neq 1}$	${\displaystyle {\begin{pmatrix}e^{i\theta /2}&0\\0&e^{-i\theta /2}\end{pmatrix}}}$	z ↦ e ^iθ z
放物線	σ = 4	k = 1	${\displaystyle {\begin{pmatrix}1&a\\0&1\end{pmatrix}}}$	z ↦ z + a
双曲線	4 < σ < ∞ ${\displaystyle \sigma =2+2\cosh(\theta )}$	${\displaystyle k\in \mathbb {R} ^{+}}$ ${\displaystyle k=e^{\pm \theta }\neq 1}$	${\displaystyle {\begin{pmatrix}e^{\theta /2}&0\\0&e^{-\theta /2}\end{pmatrix}}}$	z ↦ e ^θ z
斜航性	σ ∈ C \ [0,4] ${\displaystyle \sigma =(\lambda +\lambda ^{-1})^{2}}$	${\displaystyle |k|\neq 1}$ ${\displaystyle k=\lambda ^{2},\lambda ^{-2}}$	${\displaystyle {\begin{pmatrix}\lambda &0\\0&\lambda ^{-1}\end{pmatrix}}}$	z ↦ kz

実際の事例と用語に関する注意

実数の場合（係数が実数でなければならない場合）、非双曲的な斜航変換は存在せず、実円錐曲線の場合と同様に、楕円型、放物型、双曲型に分類されます。この用語は、トレースの絶対値の半分、|tr|/2 を変換の離心率と見なすことに起因しています。2 で割ると次元が修正されるため、恒等式の離心率は 1 になります（このため、トレースの代わりに tr/ n が使用されることがあります）。また、絶対値は、PSL で作業しているためにトレースが係数 ±1 までしか定義されていないことを修正します。あるいは、上で行ったように、トレースの半分の 2乗を離心率の 2 乗の代理として使用することもできます。これらの分類（2 乗と絶対値が異なるため、正確な離心率の値は一致しません）は、実トレースの場合は一致しますが、複素トレースの場合は一致しません。SL(2, R )（2-回被覆）の元の分類にも同じ用語が用いられ、他の分野でも同様の分類が用いられている。斜航変換は本質的に複雑な現象であり、複素離心率に対応する。

特性定数の幾何学的解釈

次の図は、球面から平面への立体変換後、非放物面の場合のメビウス変換の 2 つの固定点を示しています。

特性定数は対数で表すことができます。 このように表すと、実数ρは展開係数となります。これは、固定点γ ₁がどれだけ反発するか、そしてγ ₂がどれだけ引力を持つかを示します。実数αは回転係数であり、変換によって平面がγ _{1を中心に反時計回りに、また}γ ₂を中心に時計回りに どれだけ回転するかを示します。 $${\displaystyle e^{\rho +\alpha i}=k.}$$

楕円変換

ρ = 0の場合、固定点は引力でも斥力でもなく無差別であり、この変換は楕円型と呼ばれます。これらの変換は、すべての点を2つの固定点の周りを円運動させる傾向があります。固定点の1つが無限遠にある場合、これは点の周りをアフィン回転することと同等です。

任意の楕円メビウス変換によって生成される1パラメータ部分群をとると、部分群内のあらゆる変換が同じ2点を固定する連続変換が得られる。他のすべての点は、リーマン球面上の2つの固定点の間にある円の族に沿って移動する。一般に、2つの固定点は任意の異なる2点となり得る。

これには重要な物理的解釈があります。ある観測者が、ある軸の周りを一定の角速度で回転していると想像してください。そして、天球の北極と南極を二つの不動点とすることができます。すると、夜空の様相は、0、∞、そして観測者の一定の角速度に対応する数αを共有する楕円変換の1パラメータ部分群によって記述されるのと全く同じように、連続的に変化します。

以下は、楕円メビウス変換がリーマン球面（平面への立体投影後）に与える影響を示す図です。

これらの図は、単一のメビウス変換の効果を示しています。この変換によって生成される1パラメータ部分群は、図が示す円弧の族に沿って点を 連続的に移動させます。

双曲変換

αがゼロ（または 2 πの倍数）の場合、変換は双曲型と呼ばれます。これらの変換は、点をある固定点から別の固定点へと円軌道に沿って移動させる傾向があります。

任意の双曲型メビウス変換によって生成される1パラメータ部分群をとると、連続変換が得られ、その部分群内のどの変換でも同じ2点が固定される。他のすべての点は、最初の固定点から2番目の固定点に向かう特定の円弧の族に沿って移動する。一般に、2つの固定点はリーマン球面上の任意の異なる2点となり得る。

これにも重要な物理的解釈があります。ある観測者が天球上で北極方向に（加速度の大きさは一定で）加速していると想像してください。すると、夜空の様相は、0、∞という不動点を共有し、実数ρが観測者の加速度ベクトルの大きさに対応する双曲型変換の1パラメータ部分群によって記述されるのと全く同じように変化します。星は経線に沿って南極から北極へと移動しているように見えます。（球面から平面への立体投影では、経線は円弧として現れます。）

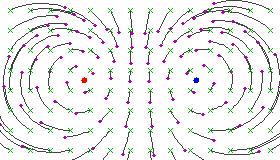
以下は、双曲型メビウス変換がリーマン球面（平面への立体投影後）に与える影響を示す図です。

これらの図は、固定点にある正と負の電荷の磁力線に似ています。これは、円形の流線が 2 つの固定点の間に一定の角度を成すためです。

斜航変換

ρとαが両方ともゼロでない場合、この変換は斜航変換と呼ばれます。これらの変換は、すべての点をS字型の経路で一方の固定点からもう一方の固定点へと移動させる傾向があります。

「航路」という言葉は、ギリシャ語の「λοξος（loxos）（斜め）」 ＋「δρόμος（dromos）（進路）」に由来します。一定の方位、例えば北東の方向を維持する場合、最終的には対数螺旋を描いて北極の周りを航行することになります。メルカトル図法では、北極と南極が無限遠に投影されるため、このような進路は直線となります。航路が経線に対してなす角度（つまり、その傾き、螺旋の「​​きつさ」）は、kの引数です。もちろん、メビウス変換では、2つの固定点は北極と南極だけでなく、どこにでも設定できます。しかし、あらゆる航路変換は、そのような航路に沿ってすべての点を移動する変換と共役になります。

任意の斜航メビウス変換によって生成される1パラメータ部分群をとると、連続変換が得られ、その部分群内のすべての変換は同じ2点を固定する。他のすべての点は、最初の固定点から離れて2番目の固定点に向かう、特定の曲線族に沿って流れる。双曲型の場合とは異なり、これらの曲線は円弧ではなく、球面から平面への立体射影の下で、一方の固定点を中心に反時計回りに無限回巻き、もう一方の固定点を中心に時計回りに無限回巻きする螺旋曲線として現れる特定の曲線である。一般に、2つの固定点は、リーマン球面上の任意の異なる2点となり得る。

2 つの固定点が 0、∞ の場合の物理的な解釈は、おそらく推測できるでしょう。ある軸の周りを回転 (一定の角速度で) し、同じ軸に沿って移動している観測者には、実際の線速度と角速度の大きさによってそれぞれ決まる固定点 0、∞、およびρ、αを持つ航程変換の 1 パラメータ サブグループに従って夜空の外観が変化するのが表示されます。

立体投影

これらの図は、メビウス変換をリーマン球面上に立体的に投影したものです。特に、球面に投影した場合、無限遠点の固定点という特殊なケースは、任意の位置に固定点がある場合と何ら変わりないように見えることに注意してください。

無限遠の1つの固定点
楕円形	双曲線	斜航性
正反対の固定点
楕円形	双曲線	斜航性
任意の場所の固定点
楕円形	双曲線	斜航性

変換の反復

変換に固定点γ ₁、γ ₂、および特性定数kがある場合、となります。 ${\displaystyle {\mathfrak {H}}}$ ${\displaystyle {\mathfrak {H}}'={\mathfrak {H}}^{n}}$ ${\displaystyle \gamma _{1}'=\gamma _{1},\gamma _{2}'=\gamma _{2},k'=k^{n}}$

これを使用して、変換を反復処理したり、ステップに分割してアニメーション化したり できます。

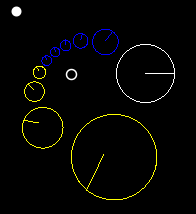
これらの画像は、さまざまな特性定数による変換で連続的に反復される 3 つのポイント (赤、青、黒) を示しています。

これらの画像は、円を双曲変換、楕円変換、斜航変換で変換すると何が起こるかを示しています。楕円変換と斜航変換の画像では、αの値は1/10です。

高次元

高次元では、メビウス変換は⁠ ⁠の同相写像、つまり⁠ ⁠の一点コンパクト化であり、球面上の反転と超平面上の反射の有限合成である。^{[ 7 ]}共形幾何学におけるリウヴィルの定理は、少なくとも3次元では、すべての共形変換はメビウス変換であると述べている。すべてのメビウス変換は、、 、は直交行列、は0または2の 形で表される。 メビウス変換の群はメビウス群とも呼ばれる。^{[ 8 ]}${\displaystyle {\overline {\mathbb {R} ^{n}}}}$ ${\displaystyle \mathbb {R} ^{n}}$ $${\displaystyle f(x)=b+{\frac {\alpha A(x-a)}{|x-a|^{\varepsilon }}},}$$ ${\displaystyle a,b\in \mathbb {R} ^{n}}$ ${\displaystyle \alpha \in \mathbb {R} }$ ${\displaystyle A}$ ${\displaystyle \varepsilon }$

向きを保存するメビウス変換は、メビウス群における恒等式の連結成分を形成する。n = 2次元においては、向きを保存するメビウス変換はまさにここで扱うリーマン球面の写像である。向きを反転させるメビウス変換は、これらから複素共役によって得られる。^{[ 9 ]}

メビウス変換の定義域、すなわち⁠ ⁠は、 ${\displaystyle {\overline {\mathbb {R} ^{n}}}}$ n次元球面と同相である。これら2つの空間間の標準的な同型はケーリー変換であり、これは⁠ ⁠のメビウス変換である。この同一視は、メビウス変換を の共形同型と考えることもできるということを意味する。n球面は、メビウス群の作用とともに、（クラインのエアランゲンプログラムの意味で）メビウス幾何学と呼ばれる幾何学的構造である。^{[ 10 ]}${\displaystyle S^{n}}$ ${\displaystyle {\overline {\mathbb {R} ^{n+1}}}}$ ${\displaystyle S^{n}}$

アプリケーション

ローレンツ変換

メビウス群とローレンツ群の同型性は、複数の著者によって指摘されている。双曲幾何学とメビウス幾何学に関連する自己同型関数に関するフェリックス・クラインの以前の研究(1893、1897) ^{[ 11 ]}に基づいて、グスタフ・ヘルグロッツ(1909) ^{[ 12 ]}は、単位球面をそれ自身に変換する双曲運動(すなわち、双曲空間の等長自己同型) がローレンツ変換に対応することを示し、これによってヘルグロッツは 1 パラメータのローレンツ変換を斜航群、楕円群、双曲群、放物群に分類することができた。他の著者としては、エミール・アルティン（1957）^{[ 13 ]} 、 HSMコクセター（1965）^{[ 14 ]}、ロジャー・ペンローズ、ヴォルフガング・リンドラー（1984）^{[ 15 ]} 、トリスタン・ニーダム（1997）^{[ 16 ]}、WMオリビア（2002）^{[ 17 ]などがいます。}

ミンコフスキー空間は、実数の4倍体（x ₀、x ₁、x ₂、x ₃）の空間からなる4次元実座標空間R ⁴と、その二次形式$${\displaystyle Q(x_{0},x_{1},x_{2},x_{3})=x_{0}^{2}-x_{1}^{2}-x_{2}^{2}-x_{3}^{2}.}$$

特殊相対論の用語を借りると、Q > 0の点は時間的 であると見なされます。さらに、x ₀ > 0の場合、その点は未来を指すと呼ばれます。 Q < 0の点は空間的 と呼ばれます。ヌルコーンS は、 Q = 0の点で構成されます。未来ヌルコーンN ⁺は、ヌルコーン上でx ₀ > 0の点です。すると天球は、初期点がR ⁴の原点であるN ⁺内の光線の集合と同一視されます。 R ⁴上の、正の行列式を持ち、二次形式Qを保存し、時間方向を保存する線型変換の集合は、制限ローレンツ群SO ⁺ (1, 3)を形成します。

天球の幾何学に関連して、変換群SO ⁺ (1, 3)は球面のメビウス変換群PSL(2, C )と同一視される。各( x ₀ , x ₁ , x ₂ , x ₃ ) ∈ R ⁴に、エルミート行列を関連付ける。$${\displaystyle X={\begin{bmatrix}x_{0}+x_{1}&x_{2}+ix_{3}\\x_{2}-ix_{3}&x_{0}-x_{1}\end{bmatrix}}.}$$

行列Xの行列式はQ ( x ₀ , x ₁ , x ₂ , x ₃ )に等しい。特殊線型群はこのような行列の空間に次のように作用する。

${\displaystyle X\mapsto AXA^{*}}$

1

それぞれのA ∈ SL(2, C )に対して成り立ち、このSL(2, C )の作用はdet A = 1なのでXの行列式を保存する。 Xの行列式は二次形式Qと同一視されるので、SL(2, C )はローレンツ変換として作用する。次元的根拠から、SL(2, C )はSO(1, 3)の単位元近傍を覆う。SL(2, C )は連結なので、制限ローレンツ群SO ⁺ (1, 3)全体を覆っている。さらに、作用 ( 1 ) の核は部分群 {± I } なので、商群へ移ることで群同型が得られる。

${\displaystyle \operatorname {PSL} (2,\mathbb {C} )\cong \operatorname {SO} ^{+}(1,3).}$

2

ここで、 ( x ₀、x ₁、x ₂、x ₃ )がゼロの場合に注目すると、行列Xの行列式はゼロになり、したがって複素2ベクトルξとその複素共役の外積として分解されます。

${\displaystyle X=\xi {\bar {\xi }}^{\text{T}}=\xi \xi ^{*}.}$

3

2成分ベクトルξは、( 1 )と整合する形でSL(2, C )の作用を受ける。これにより、 SL(2, C )のエルミート行列表現の核は{± I } であることが明らかである。

PSL(2, C )の天球への作用は、立体射影を用いて幾何学的に記述することもできる。まず、 R ^4のx ₀ = 1で与えられる超平面を考える。 天球は、超平面と将来の零円錐N ^{+の交点である球面}S ⁺と同一視できる。この球面の北極(1, 0, 0, 1)から平面x ₃ = 0への立体射影は、座標(1, x ₁ , x ₂ , x ₃ ) の点から 点 $${\displaystyle x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=1}$$ $${\displaystyle \left(1,{\frac {x_{1}}{1-x_{3}}},{\frac {x_{2}}{1-x_{3}}},0\right).}$$

複素座標 を導入すると、逆立体投影により、 S ⁺上の 点( x ₁、x ₂、x ₃ )に対して次の式が得られます。 $${\displaystyle \zeta ={\frac {x_{1}+ix_{2}}{1-x_{3}}},}$$

${\displaystyle {\begin{aligned}x_{1}&={\frac {\zeta +{\bar {\zeta }}}{\zeta {\bar {\zeta }}+1}}\\x_{2}&={\frac {\zeta -{\bar {\zeta }}}{i(\zeta {\bar {\zeta }}+1)}}\\x_{3}&={\frac {\zeta {\bar {\zeta }}-1}{\zeta {\bar {\zeta }}+1}}.\end{aligned}}}$

4

SO ⁺ (1, 3)のN ⁺上の点への作用は超平面S ^{+ を}維持しませんが、 S ⁺上の点に作用し、結果が再びS ⁺内になるように再スケーリングすると、球面上のSO ⁺ (1, 3)の作用が得られ、これは複素変数ζへの作用になります。実際には、この作用は分数線形変換によるものですが、天球のこの表現からは容易には分かりません。逆に、ζ変数の任意の分数線形変換は、適切な（一意に決定される）再スケーリングの後、おそらく N ⁺上の一意のローレンツ変換になります。

立体射影をより不変的に記述し、作用をより明確に理解するためには、変数ζ = z : w を複素射影直線CP ¹の同次座標の対の比とみなす必要がある。立体射影は、 C ² − {0}からN ⁺への変換に相当し、これは実スケーリングに関して2次の同次である。

${\displaystyle (z,w)\mapsto (x_{0},x_{1},x_{2},x_{3})=(z{\bar {z}}+w{\bar {w}},z{\bar {z}}-w{\bar {w}},z{\bar {w}}+w{\bar {z}},i^{-1}(z{\bar {w}}-w{\bar {z}}))}$

5

これは、スケールに制限すると（4 ）と一致する。（ 5 ）の成分は、外積から得られるものと全く同じである。 ${\displaystyle z{\bar {z}}+w{\bar {w}}=1.}$ $${\displaystyle {\begin{bmatrix}x_{0}+x_{1}&x_{2}+ix_{3}\\x_{2}-ix_{3}&x_{0}-x_{1}\end{bmatrix}}=2{\begin{bmatrix}z\\w\end{bmatrix}}{\begin{bmatrix}{\bar {z}}&{\bar {w}}\end{bmatrix}}.}$$

まとめると、制限ローレンツ群 SO ⁺ (1,3) の作用は、メビウス群PSL(2, C )の作用と一致する。これが次の定義の根拠となる。次元n ≥ 2において、メビウス群Möb( n ) は、球面S ⁿからそれ自身への向きを保存するすべての共形等長変換の成す群である。共形球面をミンコフスキー空間R ^1,n+1におけるヌル円錐の未来を指す光線の空間として実現することにより、時間の方向を保存する、正の行列式を持つローレンツ変換の制限ローレンツ群 SO ⁺ (1, n +1) と Möb( n )の同型が存在する。

コクセターは代わりに同等の二次形式⁠ ⁠${\displaystyle Q(x_{1},\ x_{2},\ x_{3}\ x_{4})=x_{1}^{2}+x_{2}^{2}+x_{3}^{2}-x_{4}^{2}}$ から始めました。

彼は、ローレンツ群を { x | Q( x ) = −1} が安定する変換と同一視しました。次に、 x を同次座標と解釈し、ヌルコーン { x | Q( x ) = 0}を点の双曲空間 { x | Q( x ) < 0} のケーリー絶対値と解釈しました。次に、コクセターは、 ローレンツ不変な二次曲面が球面⁠ ⁠に対応するように変数を導入しました 。コクセターは、フェリックス・クラインもこの対応について書いていて、(0, 0, 1)から複素平面への立体射影を適用していたと指摘しています。コクセターは、反転平面の円が双曲空間の平面を表し、一般的なホモグラフィーは 2 つまたは 4 つの円の反転の積であり、2 つまたは 4 つの平面の反転の積である一般的な双曲変位に対応するという事実を使用しました。 $${\displaystyle \xi ={\frac {x_{1}}{x_{4}}},\ \eta ={\frac {x_{2}}{x_{4}}},\ \zeta ={\frac {x_{3}}{x_{4}}}}$$ ${\displaystyle \xi ^{2}+\eta ^{2}+\zeta ^{2}=1}$ ${\textstyle z={\frac {\xi +i\eta }{1-\zeta }}.}$

双曲空間

上で見たように、メビウス群PSL(2, C )は、ミンコフスキー空間上で、原点、空間の向き、および時間の方向を保存する等長変換の群として作用します。正光円錐内のQ = 1となる点（双曲型3次元空間H ³のモデルを形成する）に限定すると、メビウス群はH ³上で、向きを保存する等長変換の群として作用することがわかります。実際、メビウス群は双曲型3次元空間の向きを保存する等長変換の群に等しいです。ポアンカレ球モデルを用いて、 R ³内の単位球をH ³と同一視すると、リーマン球面をH ³の「共形境界」と考えることができます。H ³の向きを保存する等長変換はすべて、リーマン球面上のメビウス変換を生じ、その逆も同様です。

参照

• 双一次変換
• 共形幾何学
• フックス群
• 一般化された円
• 双曲幾何学
• 解析関数の無限合成
• 反転変換
• クライン群
• リー球面幾何学
• 線形分数変換
• リウヴィルの定理（共形写像）
• ローレンツ群
• モジュラーグループ
• ポアンカレ半平面モデル
• 射影幾何学
• 環上の射影直線
• ローレンツ群の表現論
• ショットキーグループ
• スミスチャート

注記

1. 幾何学的には、この写像は周期4で± iの周りを90°回転する立体投影であり、${\displaystyle 0\mapsto 1\mapsto \infty \mapsto -1\mapsto 0.}$

参考文献

特定の

1. Arnold & Rogness 2008、定理 1.
2. ニーダム、トリスタン（2021年）『微分幾何学と形：五幕の数学的ドラマ』プリンストン大学出版局、p.77、脚注16。ISBN 9780691203690。
3. オルセン、ジョン、「メビウス変換の幾何学」（PDF）
4. Weisstein, Eric W.「対称点」。MathWorld 。
5. Tóth 2002、第1.2節「回転とメビウス変換」、 p. 22。
6. Tóth 2002、第1.6節、追加トピック：クラインのイコサヘドロン理論、 66ページ。
7. イワニエツ、タデウシュ、マーティン、ゲイヴン、「リウヴィルの定理、解析と位相幾何学」、339-361ページ、ワールドサイエンス出版、リバーエッジ、ニュージャージー州、1998年
8. JB Wilker (1981)「反転幾何学」、 MR 0661793 
9. Berger, Marcel (1987), Geometry II , Springer (Universitext), p. 18.10
10. Akivis, Maks; Goldberg, Vladislav (1992),共形微分幾何学とその一般化, Wiley-Interscience
11. Felix Klein (1893)、 Nicht-Euklidische Geometrie、Autogr. Voll.、ゲッティンゲン;ロバート・フリッケ& フェリックス・クライン (1897)、 Autormorphe Funktionen I.、トイブナー、ライプツィヒ
12. Herglotz, Gustav (1910) [1909]、「Über den vom Standpunkt des Relativitätsprinzips aus als starr zu bezeichnenden Körper」 [相対性原理の観点から「剛体」と指定される物体について]、Annalen der Physik (ドイツ語)、336 (2): 393– 415、ビブコード：1910AnP...336..393H、ドイ：10.1002/andp.19103360208
13. エミール・アルティン（1957）『幾何代数』204ページ
14. HSM Coxeter (1967)「ローレンツ群とホモグラフィ群」LG Kovacs & BH Neumann (編)オーストラリア国立大学キャンベラ校で開催された群論に関する国際会議議事録、1965年8月10日〜20日、 Gordon and Breach Science Publishers
15. ペンローズ＆リンドラー 1984年、8～31頁。
16. Needham, Tristan (1997). Visual Complex Analysis (PDF) . Oxford: Oxford University Press. pp.  122– 124.
17. Olivia, Waldyr Muniz (2002). 「付録B：メビウス変換とローレンツ群」.幾何力学. Springer. pp.  195– 221. ISBN 3-540-44242-1. MR  1990795 .

一般的な

• アーノルド、ダグラス・N.; ログネス、ジョナサン (2008)、「メビウス変換の解明」(PDF)、AMSの通知、55 (10): 1226– 1231
• ベアドン、アラン F. (1995)、『離散群の幾何学』、ニューヨーク：シュプリンガー・フェアラーク、ISBN 978-0-387-90788-8
• Hall, GS (2004),一般相対性理論における対称性と曲率構造、シンガポール：World Scientific、ISBN 978-981-02-1051-9(ローレンツ群のリー代数のリー部分代数の共役性までの分類については第 6 章を参照してください。)
• カトク、スヴェトラーナ(1992)、フクシアン グループ、シカゴ:University of Chicago Press、ISBN 978-0-226-42583-2第2章を参照してください。
• クライン、フェリックス（1913）[第1ドイツ語版。1884]、「イコサヘドロンおよび5次方程式の解に関する講義」、モリス、ジョージ・ギャビン（第2版）訳、ロンドン：キーガン・ポール、トレンチ、トリュブナー＆カンパニー。Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade (ドイツ語)より翻訳、Teubner、1884
• クノップ、コンラッド（1952年）、関数論の要素、ニューヨーク：ドーバー、ISBN 978-0-486-60154-0(リーマン球面、立体投影、メビウス変換の美しい入門については、この古典的な本の第 3 章から第 5 章を参照してください。)
• マンフォード、デイヴィッド；シリーズ、キャロライン；ライト、デイヴィッド（2002年）『インドラの真珠：フェリックス・クラインのビジョン』ケンブリッジ大学出版局、ISBN 978-0-521-35253-6(数学者以外の人を対象に、豊富な図解を交えて理論と結果をわかりやすく解説しています。)
• ニーダム、トリスタン（1997）、ビジュアル複素解析、オックスフォード：クラレンドンプレス、ISBN 978-0-19-853446-4(共役性までの分類を含む、メビウス変換の美しい図解による入門については、第 3 章を参照してください。)
• ペンローズ、ロジャー；リンドラー、ヴォルフガング（1984年）、スピノルと時空、第1巻：2スピノル計​​算と相対論的場、ケンブリッジ大学出版局、ISBN 978-0-521-24527-2
• シュヴェルトフェガー、ハンス（1979）、複素数の幾何学、ドーバー、ISBN 978-0-486-63830-0(メビウス変換の概要については第 2 章を参照してください。)
• トート、ガボール（2002）、有限メビウス群、球面の極小浸漬、モジュライ

さらに読む

• Lawson, MV (1998). 「メビウス逆モノイド」 . Journal of Algebra . 200 (2): 428. doi : 10.1006/jabr.1997.7242 .

外部リンク

• 「準等角写像」、数学百科事典、EMS Press、2001 [1994]
• 等角地図ギャラリー
• Weisstein, Eric W. 「線形分数変換」MathWorld。