ライトフィールド

光場（ライトフィールド）は、空間内のあらゆる点をあらゆる方向に通過する光の量を記述するベクトル関数です。あらゆる光線の空間は5次元プレノプティック関数によって与えられ、各光線の強度はその放射輝度によって与えられます。マイケル・ファラデーは、光を磁場のように場として解釈すべきだと初めて提唱しました。[ 1 ]ライトフィールドという用語は、1936年にアンドレイ・ガーシュンが3次元空間における光の放射特性に関する古典的な論文で 提唱しました。

「放射場」という用語は、類似の概念、あるいは同一の概念を指すために使用されることもあります[ 2 ] 。この用語は、神経放射場などの現代の研究で使用されています。

プレノプティック機能

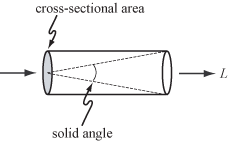
光線に沿った放射輝度L は、立体角と断面積によってサイズが決まるチューブを通るすべての可能な直線に沿って進む光の量と考えることができます。

幾何光学、すなわち非干渉性光や光の波長よりも大きな物体においては、光の基本的な媒介は光線です。光線に沿って伝わる光の量は放射輝度で、 Lで表され、W·sr −1 ·m −2の単位で測定されます。つまり、ワット(W)/ステラジアン(sr)/平方メートル(m 2 )です。ステラジアンは立体角の単位であり、平方メートルは右に示すように断面積の単位として用いられます。

3D空間内の光線を位置 ( x、y、z ) と方向 ( θ、ϕ ) でパラメータ化します。

光の不変配置によって照らされた 3 次元空間の領域におけるそのようなすべての光線に沿った放射輝度は、プレノプティック関数と呼ばれます。[ 3 ]プレノプティック照明関数は、コンピュータ ビジョンやコンピュータ グラフィックスで使用される理想的な関数であり、任意の時点における任意の視点からのシーンの画像を表します。これは実際には計算には使用されませんが、ビジョンやグラフィックスの他の概念を理解する上で概念的に役立ちます。[ 4 ]左に示すように、空間内の光線は 3 つの座標x、y、zと 2 つの角度θとϕでパラメーター化できるため、これは 5 次元関数、つまり3Dユークリッド空間と2 次元球面の積に相当する5 次元多様体上の関数です。

２つの光源I1とI2から生じる放射照度ベクトルD1とD2を合計すると、示されている大きさと方向を持つベクトルDが生成される。 [ 5 ]

空間内の各点におけるライトフィールドは、その点に当たる方向ごとに 1 つずつ、長さが放射輝度に比例するベクトルの無限の集合として扱うことができます。

これらのベクトルを任意の光の集合、あるいは球面全体にわたって積分すると、単一のスカラー値、すなわちその点における総放射照度と、結果として得られる方向が得られます。図は、2つの光源の場合のこの計算を示しています。コンピュータグラフィックスでは、この3次元空間のベクトル値関数はベクトル放射照度場と呼ばれます。[ 6 ]場内の各点におけるベクトル方向は、その点に置かれた平面が最も明るく照らされる方向として解釈できます。

高次元性

時間、波長、偏光角は追加の次元として扱うことができ、それに応じてより高次元の関数が生成されます。

4Dライトフィールド

遮るものがない場合、光線に沿った放射輝度は一定のままです。

プレノプティック関数において、対象領域に凹面物体（例えば、カップ状の手）が含まれている場合、物体上の一点から発せられた光は、物体上の別の点に遮られるまで、ごく短い距離しか進まない可能性があります。このような領域でこの関数を測定する実用的な装置は存在しません。

しかし、物体の凸包の外側にある場所（例えばシュリンクラップ）では、プレノプティック関数は複数の画像を撮影することで測定できます。この場合、光線に沿った放射輝度はその長さ全体にわたって一定であるため、関数には冗長情報が含まれます。冗長情報は正確に1次元であり、結果として4次元関数が形成されます。この関数は光場、4D光場[ 7 ] 、ルミグラフ[ 8 ]など様々な名称で呼ばれます。正式には、この場は空の空間における光線に沿った放射輝度として定義されます。

ライトフィールド内の光線集合は、様々な方法でパラメータ化できます。最も一般的な方法は、2平面パラメータ化です。このパラメータ化では、例えば2つの平面が互いに平行である場合に、それらの平面に平行な光線を表現するなど、すべての光線を表現できるわけではありませんが、透視投影画像の解析幾何学と密接に関連しています。2平面ライトフィールドを簡単に考えると、UV平面上の観測者の位置からそれぞれ撮影された、 ST平面（およびST平面をまたぐ、またはST平面の向こう側にある可能性のあるオブジェクト）の透視画像の集合体と捉えることができます。このようにパラメータ化されたライトフィールドは、ライトスラブと呼ばれることもあります。

3次元空間の空の領域を通る光の流れを表す4Dライトフィールドの、いくつかの代替パラメータ化。左：平面または曲面上の点と、各点から発せられる方向。中央：球面上の点のペア。右：一般的な（つまり任意の）位置にある2つの平面上の点のペア。

サウンドアナログ

音における4Dライトフィールドの類似物は、音場、あるいは波動場（波動場合成）であり、対応するパラメータ化はキルヒホッフ・ヘルムホルツ積分です。これは、障害物がない場合、時間経過に伴う音場は平面上の圧力によって与えられることを示しています。したがって、これは任意の時点では2次元の情報であり、時間の経過とともに3次元の場となります。

光の見かけ上の四次元性と比較すると、この二次元性は、光が光線（ある時点では0次元、時間の経過とともに1次元）として進行するのに対し、ホイヘンス・フレネルの原理によれば、音波面は球面波（ある時点では2次元、時間の経過とともに3次元）としてモデル化できるためです。つまり、光は一方向（情報の2次元）に進みますが、音はあらゆる方向に広がります。しかし、真空でない媒質を伝わる光も同様に散乱する可能性があり、散乱によって失われる不可逆性、つまり情報は、見かけ上のシステム次元の損失として識別できます。

画像の再フォーカス

ライトフィールドは空間情報と角度情報を提供するため、露光後に焦点面の位置を変更することができます。これはしばしばリフォーカスと呼ばれます。リフォーカスの原理は、積分変換を用いてライトフィールドから従来の2次元写真を得ることです。この変換はライトフィールドを入力として受け取り、特定の平面に焦点を合わせた写真を生成します。

が第1の平面上の位置から第2の平面上の位置まで移動する光線を記録する4次元光場を表し、ここでが2つの平面間の距離であると仮定すると、任意の深さでの2次元写真は、次の積分変換から得ることができる：[ 9 ]LF（s、t、あなた、v）{\displaystyle L_{F}(s,t,u,v)}（あなた、v）{\displaystyle (u,v)}（s、t）{\displaystyle (s,t)}F{\displaystyle F}αF{\displaystyle \alpha F}

Pα[LF]（s、t）＝1α2F2∬LF（あなた（1−1α）+sα、v（1−1α）+tα、あなた、v） dあなたdv{\displaystyle {\mathcal {P}}_{\alpha }\left[L_{F}\right](s,t)={1 \over \alpha ^{2}F^{2}}\iint L_{F}\left(u\left(1-{\frac {1}{\alpha }}\right)+{\frac {s}{\alpha }},v\left(1-{\frac {1}{\alpha }}\right)+{\frac {t}{\alpha }},u,v\right)~dudv}、

あるいはもっと簡潔に言えば、

Pα[LF]（s）＝1α2F2∫LF（あなた（1−1α）+sα、あなた）dあなた{\displaystyle {\mathcal {P}}_{\alpha }\left[L_{F}\right]({\boldsymbol {s}})={\frac {1}{\alpha ^{2}F^{2}}}\int L_{F}\left({\boldsymbol {u}}\left(1-{\frac {1}{\alpha }}\right)+{\frac {\boldsymbol {s}}{\alpha }},{\boldsymbol {u}}\right)d{\boldsymbol {u}}}、

ここで、、、は写真演算子です。 s=(s,t){\displaystyle {\boldsymbol {s}}=(s,t)}u=(u,v){\displaystyle {\boldsymbol {u}}=(u,v)}Pα[⋅]{\displaystyle {\mathcal {P}}_{\alpha }\left[\cdot \right]}

実際には、プレノプティックカメラは通常、光照射野の離散的なサンプルを撮影するため、この式を直接使用することはできない。そのため、を計算するには再サンプリング（または補間）が必要となる。もう一つの問題は、計算量が非常に多いことである。4次元光照射野から2次元写真を計算する場合、この式の計算量は となる。[ 9 ]LF(s,t,u,v){\displaystyle L_{F}(s,t,u,v)}LF(u(1−1α)+sα,u){\textstyle L_{F}\left({\boldsymbol {u}}\left(1-{\frac {1}{\alpha }}\right)+{\frac {\boldsymbol {s}}{\alpha }},{\boldsymbol {u}}\right)}N×N{\displaystyle N\times N}N×N×N×N{\displaystyle N\times N\times N\times N}O(N4){\displaystyle O(N^{4})}

フーリエスライス写真

計算の複雑さを軽減する一つの方法は、フーリエスライス定理の概念を採用することです。[ 9 ]写真演算子は、せん断とそれに続く投影と見なすことができます。結果は、ライトフィールドの4次元フーリエ変換の拡大された2次元スライスに比例するはずです。より正確には、ライトフィールドの4次元フーリエスペクトルから2次元スライスを抽出し、逆2次元変換を適用し、スケーリングすることで、再焦点画像を生成することができます。このアルゴリズムの漸近複雑度は です。 Pα[⋅]{\displaystyle {\mathcal {P}}_{\alpha }\left[\cdot \right]}O(N2log⁡N){\displaystyle O(N^{2}\operatorname {log} N)}

離散焦点スタック変換

2次元写真を効率的に計算するもう一つの方法は、離散焦点スタック変換（DFST）を用いることです。[ 10 ] DFSTは、再焦点化された2次元写真、いわゆるフォーカルスタックを生成するように設計されています。この手法は、高速分数フーリエ変換（FrFT） によって実装できます。

離散写真演算子は、 4次元グリッドでサンプリングされたライトフィールドに対して次のように定義されます。Pα[⋅]{\displaystyle {\mathcal {P}}_{\alpha }\left[\cdot \right]}LF(s,u){\displaystyle L_{F}({\boldsymbol {s}},{\boldsymbol {u}})}s=Δss~,{\displaystyle {\boldsymbol {s}}=\Delta s{\tilde {\boldsymbol {s}}},}s~=−ns,...,ns{\displaystyle {\tilde {\boldsymbol {s}}}=-{\boldsymbol {n}}_{\boldsymbol {s}},...,{\boldsymbol {n}}_{\boldsymbol {s}}}u=Δuu~,u~=−nu,...,nu{\displaystyle {\boldsymbol {u}}=\Delta u{\tilde {\boldsymbol {u}}},{\tilde {\boldsymbol {u}}}=-{\boldsymbol {n}}_{\boldsymbol {u}},...,{\boldsymbol {n}}_{\boldsymbol {u}}}

Pq[L](s)=∑u~=−nunuL(uq+s,u)Δu,Δu=ΔuΔv,q=(1−1α){\displaystyle {\mathcal {P}}_{q}[L]({\boldsymbol {s}})=\sum _{{\tilde {\boldsymbol {u}}}=-{\boldsymbol {n}}_{\boldsymbol {u}}}^{{\boldsymbol {n}}_{\boldsymbol {u}}}L({\boldsymbol {u}}q+{\boldsymbol {s}},{\boldsymbol {u}})\Delta {\boldsymbol {u}},\quad \Delta {\boldsymbol {u}}=\Delta u\Delta v,\quad q=\left(1-{\frac {1}{\alpha }}\right)}

通常、4D グリッド上には存在しないため、DFST は三角関数の補間を採用して非グリッド値を計算します。 (uq+s,u){\displaystyle ({\boldsymbol {u}}q+{\boldsymbol {s}},{\boldsymbol {u}})}

アルゴリズムは次のステップで構成されます。

  • サンプリング周期とでライトフィールドをサンプリングし、離散化されたライトフィールドを取得します。LF(s,u){\displaystyle L_{F}({\boldsymbol {s}},{\boldsymbol {u}})}Δs{\displaystyle \Delta s}Δu{\displaystyle \Delta u}LFd(s,u){\displaystyle L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})}
  • エイリアシングなしで FrFT に十分な信号長になるようにゼロを埋め込みます。LFd(s,u){\displaystyle L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})}
  • あらゆる について、の離散フーリエ変換を計算し、結果 を取得します。u{\displaystyle {\boldsymbol {u}}}LFd(s,u){\displaystyle L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})}R1{\displaystyle R1}
  • すべての焦点距離 に対して、の分数フーリエ変換を計算します。ここで、変換の順序は に依存し、結果 を取得します。αF{\displaystyle \alpha F}R1{\displaystyle R1}α{\displaystyle \alpha }R2{\displaystyle R2}
  • の逆離散フーリエ変換を計算します。R2{\displaystyle R2}
  • の周辺ピクセルを削除して、各2D写真のサイズをR2{\displaystyle R2}(2ns+1){\displaystyle (2{n}_{\boldsymbol {s}}+1)}(2ns+1){\displaystyle (2{n}_{\boldsymbol {s}}+1)}

ライトフィールドを作成する方法

コンピュータグラフィックスにおいて、ライトフィールドは通常、3Dモデルのレンダリングまたは実際のシーンの撮影によって生成されます。どちらの場合も、ライトフィールドを生成するには、多数の視点からのビューを取得する必要があります。パラメータ化に応じて、このビューの集合は通常、線、円、平面、球、またはその他の形状の一部にまたがりますが、非構造化の集合も可能です。[ 11 ]

ライトフィールドを写真的に捉える装置としては、移動する手持ちカメラやロボット制御のカメラ、[ 12 ]アーク状のカメラ（マトリックスで使用されたバレットタイム効果のように）、密集したカメラアレイ、[ 13 ]手持ちカメラ、[ 14 ] [ 15 ]顕微鏡、[ 16 ]またはその他の光学システムなどがあります。[ 17 ]

ライトフィールド内の画像数はアプリケーションによって異なります。ミケランジェロの「夜の女神像」 [ 18 ]のライトフィールドキャプチャには、1.3メガピクセルの画像が24,000枚含まれており、2022年時点では大規模と見なされています。ライトフィールドレンダリングで不透明な物体を完全にキャプチャするには、少なくとも前面と背面の画像を撮影する必要があります。また、st平面にまたがる物体の場合は、 （上記の2平面パラメータ化において） uv平面上で細かく間隔をあけて画像を撮影する必要があります。

ライトフィールド内の画像の数と配置、および各画像の解像度は、まとめて4Dライトフィールドの「サンプリング」と呼ばれます。[ 19 ]また、オクルージョン、 [ 20 ]照明と反射の効果も重要です。 [ 21 ]

アプリケーション

下向きの光源（FF'）は、放射照度ベクトルが外側に曲がる光場を誘起する。ゲルシュンは微積分を用いて、面上の点（P 1 、P 2 ）に当たる放射照度を計算することができた。[ 22 ]

照明工学

ガーシュンが光場を研究した理由は、様々な形状の光源を表面上に配置した場合に、表面上で観察される照明パターンを（閉じた形で）導くことであった。[ 23 ]照明工学を専門とする光学の分野は非結像光学である。[ 24 ]この分野では、流線（ガーシュンの光束線）とベクトル流束（ガーシュンの光ベクトル）の概念が広く用いられている。しかし、光場（この場合、光線を定義する位置と方向）は、一般的に位相空間とハミルトン光学によって記述される。

ライトフィールドレンダリング

シーンの4Dライトフィールドから適切な2Dスライスを抽出することで、シーンの新しいビューが可能になります。[ 25 ]ライトフィールドとスライスのパラメータ化に応じて、これらのビューは透視投影、正投影、交差スリット、[ 26 ]一般的なリニアカメラ、[ 27 ]マルチパースペクティブ、[ 28 ]またはその他の投影法になる可能性があります。ライトフィールドレンダリングは、画像ベースレンダリングの一種です。

合成絞り写真

ライトフィールド内のサンプルの適切な4Dサブセットを統合することで、有限の（つまりピンホールではない）絞りを持つカメラで撮影される視野を近似することができます。このような視野は有限の被写界深度を持ちます。この統合を行う前にライトフィールドをシアーまたはワープすることで、異なる前頭平行面[ 29 ]または斜面[ 30 ]に焦点を合わせることができます。ライトフィールドを捉えるデジタルカメラ[ 14 ]で撮影された画像は、再フォーカスが可能です。

3Dディスプレイ

各サンプルを物理空間内の適切な光線にマッピングする技術を用いてライトフィールドを提示すると、元のシーンを見ているのと同じような裸眼立体視効果が得られます。これを実現するための非デジタル技術には、インテグラルフォトグラフィー、視差パノラマグラム、ホログラフィーなどがあります。デジタル技術には、高解像度のディスプレイ画面上にレンズレットアレイを配置したり、ビデオプロジェクターアレイを用いてレンズレットアレイに画像を投影したりすることが含まれます。ビデオカメラアレイは、時間とともに変化するライトフィールドを捉えて表示することができます。これは基本的に3Dテレビシステムを構成します。[ 31 ]ライトフィールドディスプレイの現代的なアプローチでは、光学素子と圧縮計算の協調設計を探求することで、より高い解像度、高いコントラスト、広い視野などの利点を実現しています。[ 32 ]

脳画像

神経活動は、 GCaMPなどの可逆的な蛍光マーカーをニューロンに遺伝子コード化することで光学的に記録できます。GCaMPはカルシウムイオンの存在をリアルタイムで示します。光視野顕微鏡は、1フレームで全体積情報を捉えることができるため、大規模な体積内にランダムに分布する個々のニューロンの神経活動をビデオフレームレートでモニタリングすることが可能です。[ 33 ]脳組織の光学的異常や体積画像の再構成なしに、神経活動の定量的な測定が可能であり、 [ 34 ]数千個のニューロンの活動をモニタリングするために使用できます。[ 35 ]

一般化シーン再構成（GSR）

これは、一般化された光場と再照明可能な物質場を表現するシーンモデルを作成および/または改良する方法である。[ 36 ]再構成に使用されるデータには、画像、ビデオ、オブジェクトモデル、および/またはシーンモデルが含まれる。一般化された光場は、シーン内を流れる光を表現する。再照明可能な物質場は、シーンを占める物質の光相互作用特性と放射率を表現する。シーンデータ構造は、ニューラルネットワーク[ 37 ] [ 38 ] [ 39 ] や物理ベースの構造[ 40 ] [ 41 ]などを使用して実装することができる。[ 36 ]光場と物質場は、少なくとも部分的に分離されている。[ 36 ] [ 42 ]

ホログラフィックステレオグラム

ホログラフィックステレオグラムのための合成画像の生成とプリディストーションは、計算されたライトフィールドの最も初期の例の1つです。[ 43 ]

グレア低減

グレアは、カメラ本体とレンズ光学系内での光の多重散乱によって発生し、画像のコントラストを低下させます。グレアは2次元画像空間で解析されてきましたが[ 44 ] 、 4次元光線空間現象として識別することが有用です[ 45 ] 。カメラ内部の光線空間を統計的に解析することで、グレアアーティファクトの分類と除去が可能になります。光線空間では、グレアは高周波ノイズとして振る舞い、外れ値除去によって低減できます。このような解析はカメラ内部のライトフィールドをキャプチャすることで実行できますが、空間解像度の低下を招きます。均一および不均一な光線サンプリングを使用することで、画像解像度を大幅に損なうことなくグレアを低減できます[ 45 ] 。

参照

注記

  1. ^ファラデー、マイケル（2009年4月30日）「LIV. 光線振動に関する考察」『哲学雑誌』シリーズ3. 28 (188): 345– 350. doi : 10.1080/14786444608645431 . 2013年2月18日時点のオリジナルよりアーカイブ。
  2. ^ Mildenhall, Ben; Srinivasan, Pratul P; Tancik, Matthew; Barron, Jonathan T; Ramamoorthi, Ravi; Ng, Ren (2021-12-17). 「NeRF：ビュー合成のためのニューラル放射場としてのシーン表現」 Communications of the ACM . 65 (1): 99– 106. doi : 10.1145/3503250 .
  3. ^アデルソン 1991
  4. ^ウォン 2002
  5. ^ゲルシュン、図17
  6. ^アルヴォ、1994
  7. ^レボイ 1996
  8. ^ゴートラー 1996
  9. ^ a b cン、レン (2005). 「フーリエスライス写真」。ACM SIGGRAPH 2005 論文。米国ニューヨーク州ニューヨーク：ACM Press。 pp.  735–744。土井：10.1145/1186822.1073256。ISBN 978-1-4503-7825-3. S2CID  1806641 .
  10. ^ナバ、F. ペレス;マリシャル・エルナンデス、JG。ロドリゲス＝ラモス、JM（2008年8月）。「離散フォーカルスタック変換」。2008 第 16 回欧州信号処理会議: 1–5 .
  11. ^ビューラー 2001
  12. ^レボイ 2002
  13. ^奏 1998;ヤン 2002;ウィルバーン 2005
  14. ^ a b Ng 2005
  15. ^ゲオルギエフ 2006; マルワ 2013
  16. ^レボイ 2006
  17. ^ボレス 1987
  18. ^ 「ミケランジェロの『夜の像』の光のフィールド」 accademia.stanford.edu . 2022年2月8日閲覧。
  19. ^チャイ（2000）
  20. ^デュランド（2005）
  21. ^ラマムーティ（2006）
  22. ^ゲルシュン、図24
  23. ^アッシュダウン 1993
  24. ^チャベス 2015; ウィンストン 2005
  25. ^レボイ 1996; ゴートラー 1996
  26. ^ゾメット 2003
  27. ^ユウとマクミラン 2004
  28. ^ラデマッハー 1998
  29. ^イサクセン 2000
  30. ^ヴァイシュ 2005
  31. ^ジャビディ 2002; マトゥシク 2004
  32. ^ウェッツスタイン 2012, 2011; ランマン 2011, 2010
  33. ^グローセニック、2009、2017;ペレス、2015
  34. ^ペガード、2016年
  35. ^グロゼニック、2017年
  36. ^ a b cレフィングウェル、2018
  37. ^ミルデンホール、2020年
  38. ^ Rudnev, Viktor; Elgharib, Mohamed; Smith, William; Liu, Lingjie; Golyanik, Vladislav; Theobalt, Christian (2022年7月21日). 「屋外シーンの再照明のためのNeRF」. European Conference on Computer Vision (ECCV) 2022 : 1– 22. arXiv : 2112.05140 .
  39. ^ Srinivasan, Pratual; Deng, Boyang; Zhang, Xiuming; Tancik, Matthew; Mildenhall, Ben; Barron, Jonathan (2020年12月7日). 「NeRV: 再照明と視界合成のための神経反射率と可視フィールド」. CVPR : 1–12 . arXiv : 2012.03927 .
  40. ^ Yu & Fridovich-Keil、2021年
  41. ^ Kerbl, Bernhard; Kopanas, Georgios; Leimkühler, Thomas; Drettakis, George (2023-08-08). 「リアルタイム放射輝度場レンダリングのための3Dガウススプラッティング」. arXiv : 2308.04079 [ cs.GR ].
  42. ^ Zhang, Jingyang; Yao, Yao; Li, Shiwei; Liu, Jingbo; Fang, Tian; McKinnon, David; Tsin, Yanghai; Quan, Long (2023年3月30日). 「NeILF++: 形状と材質推定のための相互反射型ライトフィールド」. pp.  1– 5. arXiv : 2303.17147 [ cs.CV ].
  43. ^ハレ 1991、1994
  44. ^タルヴァラ 2007
  45. ^ a bラスカー 2008

参考文献

理論

分析

カメラ

ディスプレイ

アーカイブ

アプリケーション

「 https://en.wikipedia.org/w/index.php?title=Light_field&oldid=1332142080#The_4D_light_field」から取得