8頂点モデル

統計力学において、8頂点モデルは氷型（6頂点）モデルの一般化である。T . Bill Sutherland ^{[ 1 ]}とC. Fan & FY Wu ^{[ 2 ]}によって議論され、 Rodney Baxterによって零場の場合に解かれた。^{[ 3 ]}

説明

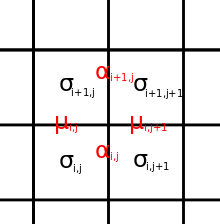
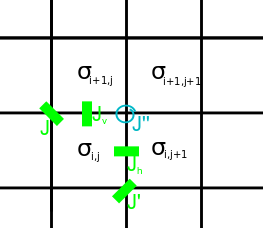
氷型モデルと同様に、8頂点モデルは正方格子モデルであり、各状態は頂点における矢印の配置によって表されます。許容される頂点は、その頂点に向かう矢印が偶数個です。これには、氷型モデルから継承された6つの矢印（1～6）、シンク（7）、およびソース（8）が含まれます。

許可される 8 つの頂点。

頂点と辺を持つ格子を考える。周期境界条件を課すと、状態7と8は状態5と6と同様に同頻度で発生することが要求され、したがって同じエネルギーを持つとみなせる。零磁場の場合、他の2つの状態ペアについても同様である。各頂点には、対応するエネルギーとボルツマン重みが与えられる。${\displaystyle N\times N}$ ${\displaystyle N^{2}}$ ${\displaystyle 2N^{2}}$ ${\displaystyle j}$ ${\displaystyle \epsilon_{j}}$

${\displaystyle w_{j}=\exp \left(-{\frac {\epsilon _{j}}{k_{\mathrm {B} }T}}\right)}$

格子上の 分割関数は次のように表される。

${\displaystyle Z=\sum \exp \left(-{\frac {\sum _{j}n_{j}\epsilon _{j}}{k_{\mathrm {B} }T}}\right)}$

ここで、外積和は格子内の頂点の許容される配置すべてにわたっている。この一般的な形式では、分割関数は未解決のままである。

ゼロ磁場の場合の解

このモデルの零電場ケースは、物理的には外部電場が存在しない状態に対応する。したがって、すべての矢印を反転させてもモデルは変化しない。したがって、状態1と2、および状態3と4は必ずペアで発生する。頂点には任意の重みを割り当てることができる。

${\displaystyle {\begin{aligned}w_{1}=w_{2}&=a\\w_{3}=w_{4}&=b\\w_{5}=w_{6}&=c\\w_{7}=w_{8}&=d.\end{aligned}}}$

この解は、4つのボルツマン重みの特定のパラメータ化に対して、転送行列の行が交換するという観察に基づいています。これは、楕円シータ関数を用いた6頂点モデルの代替解の修正として生まれました。

通勤転送行列

証明は、 およびのとき、量 ${\displaystyle \Delta '=\Delta }$ ${\displaystyle \Gamma '=\Gamma }$

${\displaystyle {\begin{aligned}\Delta &={\frac {a^{2}+b^{2}-c^{2}-d^{2}}{2(ab+cd)}}\\\Gamma &={\frac {ab-cd}{ab+cd}}\end{aligned}}}$

転送行列と（重み、 、、および、、、に関連付けられている）は交換可能である。星型三角形の関係を用いて、バクスターはこの条件を重みのパラメータ化と等価であると再定式化した 。${\displaystyle T}$ ${\displaystyle T'}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle d}$ ${\displaystyle a'}$ ${\displaystyle b'}$ ${\displaystyle c'}$ ${\displaystyle d'}$

${\displaystyle a:b:c:d=\operatorname {snh} (\eta -u):\operatorname {snh} (\eta +u):\operatorname {snh} (2\eta ):k\operatorname {snh} (2\eta )\operatorname {snh} (\eta -u)\operatorname {snh} (\eta +u)}$

固定係数と可変係数に対して。ここでsnhはsnの双曲線類似体であり、次式で表される。 ${\displaystyle k}$ ${\displaystyle \eta }$ ${\displaystyle u}$

${\displaystyle {\begin{aligned}\operatorname {snh} (u)&=-i\operatorname {sn} (iu)=i\operatorname {sn} (-iu)\\{\text{where }}\operatorname {sn} (u)&={\frac {H(u)}{{\sqrt {k}}\Theta (u)}}\end{aligned}}}$

およびおよび は係数 のシータ関数である。したがって、関連する転送行列はのみの関数である。すべての に対して、${\displaystyle H(u)}$ ${\displaystyle \Theta (u)}$ ${\displaystyle k}$ ${\displaystyle T}$ ${\displaystyle u}$ ${\displaystyle u}$ ${\displaystyle v}$

${\displaystyle T(u)T(v)=T(v)T(u).}$

行列関数${\displaystyle Q(u)}$

解のもう一つの重要な部分は、すべての複素数に対して行列が互いに可換であり、転送行列が可換であり、 ${\displaystyle Q}$ ${\displaystyle u}$ ${\displaystyle Q(u),Q(u')}$

${\displaystyle \zeta (u)T(u)Q(u)=\phi (u-\eta )Q(u+2\eta )+\phi (u+\eta )Q(u-2\eta )}$

1

どこ

${\displaystyle {\begin{aligned}\zeta (u)&=[c^{-1}H(2\eta )\Theta (u-\eta )\Theta (u+\eta )]^{N}\\\phi (u)&=[\Theta (0)H(u)\Theta (u)]^{N}.\end{aligned}}}$

このような関数の存在と交換関係は、6 頂点モデルと同様に、頂点を通る対の伝播とシータ関数の周期関係を考慮することによって実証されます。

明示的な解

（ 1 ）の行列の交換により対角化が可能となり、固有値を求めることができる。分配関数は最大固有値から計算され、その結果、サイトあたりの 自由エネルギーは

${\displaystyle {\begin{aligned}f=\epsilon _{5}-2kT\sum _{n=1}^{\infty }{\frac {\sinh ^{2}((\tau -\lambda )n)(\cosh(n\lambda )-\cosh(n\alpha ))}{n\sinh(2n\tau )\cosh(n\lambda )}}\end{aligned}}}$

のために

${\displaystyle {\begin{aligned}\tau &={\frac {\pi K'}{2K}}\\\lambda &={\frac {\pi \eta }{iK}}\\\alpha &={\frac {\pi u}{iK}}\end{aligned}}}$

ここで、 およびは、係数およびの完全楕円積分である。8頂点モデルは準結晶においても解かれた。 ${\displaystyle K}$ ${\displaystyle K'}$ ${\displaystyle k}$ ${\displaystyle k'}$

イジングモデルとの同値性

8頂点モデルと、2スピンおよび4スピンの最近傍相互作用を持つイジングモデルとの間には自然な対応関係がある。このモデルの状態は、正方格子の面上のスピンである。8頂点モデルにおける「辺」に相当するものは、隣接する面上のスピンの積である。 ${\displaystyle \sigma =\pm 1}$

${\displaystyle {\begin{aligned}\alpha _{ij}&=\sigma _{ij}\sigma _{i,j+1}\\\mu _{ij}&=\sigma _{ij}\sigma _{i+1,j}.\end{aligned}}}$

このモデルのエネルギーの最も一般的な形は

${\displaystyle {\begin{aligned}\epsilon &=-\sum _{ij}(J_{h}\mu _{ij}+J_{v}\alpha _{ij}+J\alpha _{ij}\mu _{ij}+J'\alpha _{i+1,j}\mu _{ij}+J''\alpha _{ij}\alpha _{i+1,j})\end{aligned}}}$

ここで、、、は水平、垂直、および2つの対角線の2スピン相互作用を表し、は頂点の4つの面間の4スピン相互作用を表します。合計は格子全体にわたります。 ${\displaystyle J_{h}}$ ${\displaystyle J_{v}}$ ${\displaystyle J}$ ${\displaystyle J'}$ ${\displaystyle J''}$

8頂点モデルにおいて、水平スピンと垂直スピン（辺上の矢印）をそれぞれ と表記し、上と右を正方向と定義します。頂点状態に対する制約は、頂点における4辺の積が1であるというものです。これはイジング「辺」に対して自動的に成り立ちます。各構成は一意の 、構成に対応しますが、各 、構成は2つの構成の選択肢を提供します。 ${\displaystyle \mu }$ ${\displaystyle \alpha }$ ${\displaystyle \sigma }$ ${\displaystyle \mu }$ ${\displaystyle \alpha }$ ${\displaystyle \mu }$ ${\displaystyle \alpha }$ ${\displaystyle \sigma }$

各頂点のボルツマン重みの一般形を等しくすると、と、、、の間の次の関係が格子モデル間の対応を定義します。 ${\displaystyle j}$ ${\displaystyle \epsilon _{j}}$ ${\displaystyle J_{h}}$ ${\displaystyle J_{v}}$ ${\displaystyle J}$ ${\displaystyle J'}$ ${\displaystyle J''}$

${\displaystyle {\begin{aligned}\epsilon _{1}&=-J_{h}-J_{v}-J-J'-J'',\quad \epsilon _{2}=J_{h}+J_{v}-J-J'-J''\\\epsilon _{3}&=-J_{h}+J_{v}+J+J'-J'',\quad \epsilon _{4}=J_{h}-J_{v}+J+J'-J''\\\epsilon _{5}&=\epsilon _{6}=J-J'+J''\\\epsilon _{7}&=\epsilon _{8}=-J+J'+J''.\end{aligned}}}$

したがって、8 頂点モデルのゼロ フィールドの場合、対応する Ising モデルにおける水平および垂直の相互作用は消滅します。

これらの関係は、8頂点モデルと(2,4)スピンイジングモデルの分配関数の 等価性を与える。したがって、どちらかのモデルの解は、他方のモデルの解に直接つながる。${\displaystyle Z_{I}=2Z_{8V}}$

参照

• 6頂点モデル
• 転送行列法
• イジングモデル

注記

1. サザーランド、ビル (1970). 「氷則に従わない二次元水素結合結晶」.ジャーナル・オブ・マスマティカル・フィジックス. 11 (11). AIP Publishing: 3183– 3186. Bibcode : 1970JMP....11.3183S . doi : 10.1063/1.1665111 . ISSN  0022-2488 .
2. Fan, Chungpeng; Wu, FY (1970-08-01). 「相転移の一般格子モデル」. Physical Review B. 2 ( 3). American Physical Society (APS): 723– 733. Bibcode : 1970PhRvB...2..723F . doi : 10.1103/physrevb.2.723 . ISSN 0556-2805 . 
3. Baxter, RJ (1971-04-05). 「格子統計における8頂点モデル」. Physical Review Letters . 26 (14). American Physical Society (APS): 832– 833. Bibcode : 1971PhRvL..26..832B . doi : 10.1103/physrevlett.26.832 . ISSN 0031-9007 . 

参考文献

• バクスター、ロドニー J. (1982)、統計力学における厳密解モデル(PDF)、ロンドン：Academic Press Inc. [Harcourt Brace Jovanovich Publishers]、ISBN 978-0-12-083180-7, MR  0690578 , 2021年4月14日にオリジナル（PDF）からアーカイブ、 2012年8月12日取得