物理学において、エアリー関数 (あるいは第一種エアリー関数 )Ai( x ) ジョージ・ビデル・エアリー(1801–1892)にちなんで名付けられた 特殊関数 である。関数Ai( x )と関連関数Bi( x ) は、エアリー方程式 またはストークス方程式 として知られる微分方程式の 線形独立な 解である。 d 2 y d × 2 − × y = 0 、 {\displaystyle {\frac {d^{2}y}{dx^{2}}}-xy=0,}
線型微分方程式の解はk <0 では振動型、 k >0 では指数型となるため、エアリー関数はx <0では振動型、 x >0 では指数型となる。実際、エアリー方程式は、解の性質が振動型から指数型に変化する転換点を持つ 最も単純な2階線型微分方程式である。 d 2 y d × 2 − け y = 0 {\displaystyle {\frac {d^{2}y}{dx^{2}}}-ky=0}
Mathematica 13.1 の ComplexPlot3D 関数を使用して、複素平面における-2 - 2 i から2 + 2 i Ai( z )のカラープロットを作成しました。 Mathematica 13.1 の ComplexPlot3D 関数を使用して、複素平面における-2 - 2 i から2 + 2 i Ai'( z )の導関数を色付きでプロットしました。
定義 Ai( x ) を赤、Bi( x ) を青でプロットx の実数値に対して、第一種エアリー関数は、不定 リーマン積分 によって定義され、 これはディリクレの判定 によって収束する。任意の実数 x に対して、区間 において連続かつ有界でない導関数を持つ、増加、有界でない凸関数となる正の実数M が存在する。この区間における積分の収束は、次の代入の後にディリクレの判定によって証明できる。愛 ( × ) = 1 π ∫ 0 ∞ コス ( t 3 3 + × t ) d t ≡ 1 π リム b → ∞ ∫ 0 b コス ( t 3 3 + × t ) d t 、 {\displaystyle \operatorname {Ai} (x)={\dfrac {1}{\pi }}\int _{0}^{\infty }\cos \left({\dfrac {t^{3}}{3}}+xt\right)\,dt\equiv {\dfrac {1}{\pi }}\lim _{b\to \infty }\int _{0}^{b}\cos \left({\dfrac {t^{3}}{3}}+xt\right)\,dt,} t 3 3 + × t {\textstyle {\tfrac {t^{3}}{3}}+xt} [ M 、 ∞ ) 。 {\displaystyle [M,\infty ).} あなた = t 3 3 + × t 。 {\textstyle u={\tfrac {t^{3}}{3}}+xt.}
y = Ai( x )線形独立な 解が存在する。スカラー乗算 を除けば、 Ai( x )は x → ∞ のときにy → 0 となる条件を満たす解である。もう一方の解として標準的な選択肢は、第二種エアリー関数 Bi( x ) である。これは、 x → −∞ のときにAi( x ) と同じ振幅を持ち、位相がπ /2 だけ異なる解として定義される。 y ″ − × y = 0。 {\displaystyle y''-xy=0.}
Mathematica 13.1 の ComplexPlot3D 関数を使用して、複素平面における-2 - 2 i から2 + 2 i Bi( z )の色付きプロットを作成しました。 バイ ( × ) = 1 π ∫ 0 ∞ [ 経験 ( − t 3 3 + × t ) + 罪 ( t 3 3 + × t ) ] d t 。 {\displaystyle \operatorname {Bi} (x)={\frac {1}{\pi }}\int _{0}^{\infty }\left[\exp \left(-{\tfrac {t^{3}}{3}}+xt\right)+\sin \left({\tfrac {t^{3}}{3}}+xt\right)\,\right]dt.}
Mathematica 13.1 の ComplexPlot3D 関数を使用して、複素平面におけるエアリー関数Bi'( z ) の微分を-2 - 2 i から2 + 2 i までカラーでプロットしました。
プロパティ Ai( x ) とBi( x ) の値と、 x = 0Γは ガンマ関数 を表す。したがって、Ai( x ) とBi( x ) のロンスキアンは 1/ π 愛 ( 0 ) = 1 3 2 / 3 Γ ( 2 3 ) 、 愛 ′ ( 0 ) = − 1 3 1 / 3 Γ ( 1 3 ) 、 バイ ( 0 ) = 1 3 1 / 6 Γ ( 2 3 ) 、 バイ ′ ( 0 ) = 3 1 / 6 Γ ( 1 3 ) 。 {\displaystyle {\begin{aligned}\operatorname {Ai} (0)&{}={\frac {1}{3^{2/3}\,\Gamma \!\left({\frac {2}{3}}\right)}},&\quad \operatorname {Ai} '(0)&{}=-{\frac {1}{3^{1/3}\,\Gamma \!\left({\frac {1}{3}}\right)}},\\\operatorname {Bi} (0)&{}={\frac {1}{3^{1/6}\,\Gamma \!\left({\frac {2}{3}}\right)}},&\quad \operatorname {Bi} '(0)&{}={\frac {3^{1/6}}{\Gamma \!\left({\frac {1}{3}}\right)}}.\end{aligned}}}
x が正のとき、Ai( x )は正の 凸 関数で、指数関数的にゼロに向かって減少します。一方、Bi( x ) は正の凸関数で、指数関数的に増加します。x が負のとき、 Ai ( x ) とBi( x ) はゼロ付近で振動し、周波数は増加し続け、振幅は減少し続けます。これは、エアリー関数の以下の漸近公式によって裏付けられています。
エアリー関数は、 不定リーマン積分を使用する という意味で 直交[ 1 ]である。 ∫ − ∞ ∞ 愛 ( t + × ) 愛 ( t + y ) d t = δ ( × − y ) {\displaystyle \int _{-\infty }^{\infty }\operatorname {Ai} (t+x)\operatorname {Ai} (t+y)dt=\delta (xy)}
Ai( x ) とその導関数Ai'( x ) の実零点Ai( x ) とその導関数 Ai'( x ) はどちらも正の実零点を持たない。「最初の」実零点(つまり x=0 に最も近い)は以下の通りである: [ 2 ]
Ai( x ) の「最初の」零点はx ≈ −2.33811、−4.08795、−5.52056、−6.78671、... です。その導関数Ai'( x )の「最初の」零点は x ≈ −1.01879、−3.24820、−4.82010、−6.16331、... である。
Ai(青)とAi(マゼンタ)の正弦波/指数漸近形 Bi(青)とBi(マゼンタ)の正弦波/指数漸近形 後述するように、エアリー関数は複素平面 に拡張することができ、整関数となる。 | z |が arg ( z )arg( z ) に依存する。これはストークス現象 と呼ばれる。| arg( z ) | < π の場合、 Ai( z ) の漸近的な式 は次のようになる:[ 3 ]
愛 ( z ) 〜 1 2 π z 1 / 4 経験 ( − 2 3 z 3 / 2 ) [ ∑ n = 0 ∞ ( − 1 ) n Γ ( n + 5 6 ) Γ ( n + 1 6 ) ( 3 4 ) n 2 π n ! z 3 n / 2 ] 。 {\displaystyle \operatorname {Ai} (z)\sim {\dfrac {1}{2{\sqrt {\pi }}\,z^{1/4}}}\exp \left(-{\frac {2}{3}}z^{3/2}\right)\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\,\Gamma \!\left(n+{\frac {5}{6}}\right)\,\Gamma \!\left(n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{n}}{2\pi \,n!\,z^{3n/2}}}\right].} [ 4 ] Bi( z ) にも同様の式があるが、| arg( z ) |< π /3 の場合にのみ適用可能である。 愛 ( z ) 〜 e − ζ 4 π 3 / 2 z 1 / 4 [ ∑ n = 0 ∞ Γ ( n + 5 6 ) Γ ( n + 1 6 ) n ! ( − 2 ζ ) n ] 。 {\displaystyle \operatorname {Ai} (z)\sim {\dfrac {e^{-\zeta }}{4\pi ^{3/2}\,z^{1/4}}}\left[\sum _{n=0}^{\infty }{\dfrac {\Gamma \!\left(n+{\frac {5}{6}}\right)\,\Gamma \!\left(n+{\frac {1}{6}}\right)}{n!(-2\zeta )^{n}}}\right].} ζ = 2 3 z 3 / 2 。 {\displaystyle \zeta ={\tfrac {2}{3}}z^{3/2}.} 愛 ( z ) = e − ζ 2 π 1 / 2 z 1 / 4 ( 1 − 5 72 ζ + 385 10368 ζ 2 + お ( ζ − 3 ) ) {\displaystyle \operatorname {Ai} (z)={\frac {e^{-\zeta }}{2\pi ^{1/2}z^{1/4}}}\left(1-{\frac {5}{72\zeta }}+{\frac {385}{10368\zeta ^{2}}}+O(\zeta ^{-3})\right)}
バイ ( z ) 〜 1 π z 1 / 4 経験 ( 2 3 z 3 / 2 ) [ ∑ n = 0 ∞ Γ ( n + 5 6 ) Γ ( n + 1 6 ) ( 3 4 ) n 2 π n ! z 3 n / 2 ] 。 {\displaystyle \operatorname {Bi} (z)\sim {\frac {1}{{\sqrt {\pi }}\,z^{1/4}}}\exp \left({\frac {2}{3}}z^{3/2}\right)\left[\sum _{n=0}^{\infty }{\dfrac {\Gamma \!\left(n+{\frac {5}{6}}\right)\,\Gamma \!\left(n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{n}}{2\pi \,n!\,z^{3n/2}}}\right].} π /3 < | arg( z ) | < π Ai( z ) とBi( z ) の より正確な式、または、 | arg( z ) | < 2 π /3 だがゼロではない場合のAi (− z ) とBi ( − z ) のより正確 な [ 3 ] [ 5 ] Ai ( − z ) ∼ 1 π z 1 / 4 sin ( 2 3 z 3 / 2 + π 4 ) [ ∑ n = 0 ∞ ( − 1 ) n Γ ( 2 n + 5 6 ) Γ ( 2 n + 1 6 ) ( 3 4 ) 2 n 2 π ( 2 n ) ! z 3 n ] − 1 π z 1 / 4 cos ( 2 3 z 3 / 2 + π 4 ) [ ∑ n = 0 ∞ ( − 1 ) n Γ ( 2 n + 11 6 ) Γ ( 2 n + 7 6 ) ( 3 4 ) 2 n + 1 2 π ( 2 n + 1 ) ! z 3 n + 3 / 2 ] Bi ( − z ) ∼ 1 π z 1 / 4 cos ( 2 3 z 3 / 2 + π 4 ) [ ∑ n = 0 ∞ ( − 1 ) n Γ ( 2 n + 5 6 ) Γ ( 2 n + 1 6 ) ( 3 4 ) 2 n 2 π ( 2 n ) ! z 3 n ] + 1 π z 1 4 sin ( 2 3 z 3 / 2 + π 4 ) [ ∑ n = 0 ∞ ( − 1 ) n Γ ( 2 n + 11 6 ) Γ ( 2 n + 7 6 ) ( 3 4 ) 2 n + 1 2 π ( 2 n + 1 ) ! z 3 n + 3 / 2 ] . {\displaystyle {\begin{aligned}\operatorname {Ai} (-z)\sim &{}\ {\frac {1}{{\sqrt {\pi }}\,z^{1/4}}}\sin \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {5}{6}}\right)\,\Gamma \!\left(2n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{2n}}{2\pi \,(2n)!\,z^{3n}}}\right]\\[6pt]&{}-{\frac {1}{{\sqrt {\pi }}\,z^{1/4}}}\cos \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {11}{6}}\right)\,\Gamma \!\left(2n+{\frac {7}{6}}\right)\left({\frac {3}{4}}\right)^{2n+1}}{2\pi \,(2n+1)!\,z^{3n\,+\,3/2}}}\right]\\[6pt]\operatorname {Bi} (-z)\sim &{}{\frac {1}{{\sqrt {\pi }}\,z^{1/4}}}\cos \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {5}{6}}\right)\,\Gamma \!\left(2n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{2n}}{2\pi \,(2n)!\,z^{3n}}}\right]\\[6pt]&{}+{\frac {1}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\sin \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {11}{6}}\right)\,\Gamma \!\left(2n+{\frac {7}{6}}\right)\left({\frac {3}{4}}\right)^{2n+1}}{2\pi \,(2n+1)!\,z^{3n\,+\,3/2}}}\right].\end{aligned}}}
| arg( z ) | = 0 のとき、これらは良好な近似値であるが、漸近的ではない。なぜなら、正弦または余弦がゼロになるたびに、 Ai(− z ) またはBi(− z ) と上記の近似値の比は無限大になるからである。これらの極限に対する漸近展開も利用可能である。これらは Abramowitz and Stegun (1983) [ 6 ] [ 7 ]
導関数Ai'(z) とBi'(z) の漸近的な表現も得ることができる。前述と同様に、| arg( z ) | < πの とき:[ 5 ]
Ai ′ ( z ) ∼ − z 1 / 4 2 π exp ( − 2 3 z 3 / 2 ) [ ∑ n = 0 ∞ 1 + 6 n 1 − 6 n ( − 1 ) n Γ ( n + 5 6 ) Γ ( n + 1 6 ) ( 3 4 ) n 2 π n ! z 3 n / 2 ] . {\displaystyle \operatorname {Ai} '(z)\sim -{\dfrac {z^{1/4}}{2{\sqrt {\pi }}\,}}\exp \left(-{\frac {2}{3}}z^{3/2}\right)\left[\sum _{n=0}^{\infty }{\frac {1+6n}{1-6n}}{\dfrac {(-1)^{n}\,\Gamma \!\left(n+{\frac {5}{6}}\right)\,\Gamma \!\left(n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{n}}{2\pi \,n!\,z^{3n/2}}}\right].}
| arg( z ) | < π /3 のとき、次式が得られる: [ 5 ]
Bi ′ ( z ) ∼ z 1 / 4 π exp ( 2 3 z 3 / 2 ) [ ∑ n = 0 ∞ 1 + 6 n 1 − 6 n Γ ( n + 5 6 ) Γ ( n + 1 6 ) ( 3 4 ) n 2 π n ! z 3 n / 2 ] . {\displaystyle \operatorname {Bi} '(z)\sim {\frac {z^{1/4}}{{\sqrt {\pi }}\,}}\exp \left({\frac {2}{3}}z^{3/2}\right)\left[\sum _{n=0}^{\infty }{\frac {1+6n}{1-6n}}{\dfrac {\Gamma \!\left(n+{\frac {5}{6}}\right)\,\Gamma \!\left(n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{n}}{2\pi \,n!\,z^{3n/2}}}\right].}
同様に、 | arg( z ) | < 2 π /3 かつ 0 ではない場合のAi'(− z ) とBi'(− z ) の式は[ 5 ]である。
Ai ′ ( − z ) ∼ − z 1 / 4 π cos ( 2 3 z 3 / 2 + π 4 ) [ ∑ n = 0 ∞ 1 + 12 n 1 − 12 n ( − 1 ) n Γ ( 2 n + 5 6 ) Γ ( 2 n + 1 6 ) ( 3 4 ) 2 n 2 π ( 2 n ) ! z 3 n ] − z 1 / 4 π sin ( 2 3 z 3 / 2 + π 4 ) [ ∑ n = 0 ∞ 7 + 12 n − 5 − 12 n ( − 1 ) n Γ ( 2 n + 11 6 ) Γ ( 2 n + 7 6 ) ( 3 4 ) 2 n + 1 2 π ( 2 n + 1 ) ! z 3 n + 3 / 2 ] Bi ′ ( − z ) ∼ z 1 / 4 π sin ( 2 3 z 3 / 2 + π 4 ) [ ∑ n = 0 ∞ 1 + 12 n 1 − 12 n ( − 1 ) n Γ ( 2 n + 5 6 ) Γ ( 2 n + 1 6 ) ( 3 4 ) 2 n 2 π ( 2 n ) ! z 3 n ] − z 1 / 4 π cos ( 2 3 z 3 / 2 + π 4 ) [ ∑ n = 0 ∞ 7 + 12 n − 5 − 12 n ( − 1 ) n Γ ( 2 n + 11 6 ) Γ ( 2 n + 7 6 ) ( 3 4 ) 2 n + 1 2 π ( 2 n + 1 ) ! z 3 n + 3 / 2 ] {\displaystyle {\begin{aligned}\operatorname {Ai} '(-z)\sim &{}-{\frac {z^{1/4}}{{\sqrt {\pi }}\,}}\cos \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\frac {1+12n}{1-12n}}{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {5}{6}}\right)\,\Gamma \!\left(2n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{2n}}{2\pi \,(2n)!\,z^{3n}}}\right]\\[6pt]&{}-{\frac {z^{1/4}}{{\sqrt {\pi }}\,}}\sin \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\frac {7+12n}{-5-12n}}{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {11}{6}}\right)\,\Gamma \!\left(2n+{\frac {7}{6}}\right)\left({\frac {3}{4}}\right)^{2n+1}}{2\pi \,(2n+1)!\,z^{3n\,+\,3/2}}}\right]\\[6pt]\operatorname {Bi} '(-z)\sim &{}\ {\frac {z^{1/4}}{{\sqrt {\pi }}\,}}\sin \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\frac {1+12n}{1-12n}}{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {5}{6}}\right)\,\Gamma \!\left(2n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{2n}}{2\pi \,(2n)!\,z^{3n}}}\right]\\[6pt]&{}-{\frac {z^{1/4}}{{\sqrt {\pi }}\,}}\cos \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\frac {7+12n}{-5-12n}}{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {11}{6}}\right)\,\Gamma \!\left(2n+{\frac {7}{6}}\right)\left({\frac {3}{4}}\right)^{2n+1}}{2\pi \,(2n+1)!\,z^{3n\,+\,3/2}}}\right]\\\end{aligned}}}
複雑な議論 エアリー関数の定義を複素平面に拡張すると、 積分は無限遠点から偏 角 π /3 で始まり、無限遠点から偏角π/3で終わる経路Cに沿って行われます。あるいは、微分方程式 y " − xy = 0を用いて、 Ai( x ) とBi( x )を複素平面上の 関数全体 に拡張することもできます。 Ai ( z ) = 1 2 π i ∫ C exp ( t 3 3 − z t ) d t , {\displaystyle \operatorname {Ai} (z)={\frac {1}{2\pi i}}\int _{C}\exp \left({\tfrac {t^{3}}{3}}-zt\right)\,dt,}
Ai( x ) の漸近公式は、x 2/3 x が 負の実軸から離れて有界である場合でも、複素平面上で有効です。Bi ( x )の公式は、 x が 正の δ に対してセクター内にある場合に有効です。最後に、 Ai(− x ) とBi(− x ) の公式は、x が x ∈ C : | arg ( x ) | < π 3 − δ {\displaystyle x\in \mathbb {C} :\left|\arg(x)\right|<{\tfrac {\pi }{3}}-\delta } x ∈ C : | arg ( x ) | < 2 π 3 − δ . {\displaystyle x\in \mathbb {C} :\left|\arg(x)\right|<{\tfrac {2\pi }{3}}-\delta .}
エアリー関数の漸近的挙動から、Ai( x ) とBi( x ) はともに負の実軸上に無限個の零点を持つことがわかる。関数Ai( x ) は複素平面上に他の零点を持たないが、関数Bi( x ) はセクター上にも無限個の零点を持つ。z ∈ C : π 3 < | arg ( z ) | < π 2 . {\displaystyle z\in \mathbb {C} :{\tfrac {\pi }{3}}<\left|\arg(z)\right|<{\tfrac {\pi }{2}}.}
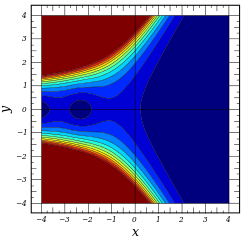
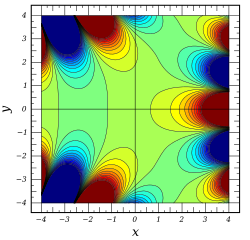
プロット ℜ [ Ai ( x + i y ) ] {\displaystyle \Re \left[\operatorname {Ai} (x+iy)\right]} ℑ [ Ai ( x + i y ) ] {\displaystyle \Im \left[\operatorname {Ai} (x+iy)\right]} | Ai ( x + i y ) | {\displaystyle \left|\operatorname {Ai} (x+iy)\right|\,} arg [ Ai ( x + i y ) ] {\displaystyle \operatorname {arg} \left[\operatorname {Ai} (x+iy)\right]\,}
ℜ [ Bi ( x + i y ) ] {\displaystyle \Re \left[\operatorname {Bi} (x+iy)\right]} ℑ [ Bi ( x + i y ) ] {\displaystyle \Im \left[\operatorname {Bi} (x+iy)\right]} | Bi ( x + i y ) | {\displaystyle \left|\operatorname {Bi} (x+iy)\right|\,} arg [ Bi ( x + i y ) ] {\displaystyle \operatorname {arg} \left[\operatorname {Bi} (x+iy)\right]\,}
他の特殊関数との関係 正の引数に対して、エアリー関数は修正ベッセル関数 と関連している。 ここで、I ±1/3 K 1/3 Ai ( x ) = 1 π x 3 K 1 / 3 ( 2 3 x 3 / 2 ) , Bi ( x ) = x 3 [ I 1 / 3 ( 2 3 x 3 / 2 ) + I − 1 / 3 ( 2 3 x 3 / 2 ) ] . {\displaystyle {\begin{aligned}\operatorname {Ai} (x)&{}={\frac {1}{\pi }}{\sqrt {\frac {x}{3}}}\,K_{1/3}\!\left({\frac {2}{3}}x^{3/2}\right),\\\operatorname {Bi} (x)&{}={\sqrt {\frac {x}{3}}}\left[I_{1/3}\!\left({\frac {2}{3}}x^{3/2}\right)+I_{-1/3}\!\left({\frac {2}{3}}x^{3/2}\right)\right].\end{aligned}}} x 2 y ″ + x y ′ − ( x 2 + 1 9 ) y = 0. {\displaystyle x^{2}y''+xy'-\left(x^{2}+{\tfrac {1}{9}}\right)y=0.}
エアリー関数の1階微分は A i ′ ( x ) = − x π 3 K 2 / 3 ( 2 3 x 3 / 2 ) . {\displaystyle \operatorname {Ai'} (x)=-{\frac {x}{\pi {\sqrt {3}}}}\,K_{2/3}\!\left({\frac {2}{3}}x^{3/2}\right).}
関数K 1/3 K 2/3 [ 8 ] (修正ベッセル関数 も参照)
負の引数の場合、エアリー関数はベッセル関数 と関連している。 ここで、J ±1/3 Ai ( − x ) = x 9 [ J 1 / 3 ( 2 3 x 3 / 2 ) + J − 1 / 3 ( 2 3 x 3 / 2 ) ] , Bi ( − x ) = x 3 [ J − 1 / 3 ( 2 3 x 3 / 2 ) − J 1 / 3 ( 2 3 x 3 / 2 ) ] . {\displaystyle {\begin{aligned}\operatorname {Ai} (-x)&{}={\sqrt {\frac {x}{9}}}\left[J_{1/3}\!\left({\frac {2}{3}}x^{3/2}\right)+J_{-1/3}\!\left({\frac {2}{3}}x^{3/2}\right)\right],\\\operatorname {Bi} (-x)&{}={\sqrt {\frac {x}{3}}}\left[J_{-1/3}\!\left({\frac {2}{3}}x^{3/2}\right)-J_{1/3}\!\left({\frac {2}{3}}x^{3/2}\right)\right].\end{aligned}}} x 2 y ″ + x y ′ + ( x 2 − 1 9 ) y = 0. {\displaystyle x^{2}y''+xy'+\left(x^{2}-{\frac {1}{9}}\right)y=0.}
スコアラー関数 Hi( x ) と-Gi( x ) は方程式y " − xy = 1/πGi ( x ) = Bi ( x ) ∫ x ∞ Ai ( t ) d t + Ai ( x ) ∫ 0 x Bi ( t ) d t , Hi ( x ) = Bi ( x ) ∫ − ∞ x Ai ( t ) d t − Ai ( x ) ∫ − ∞ x Bi ( t ) d t . {\displaystyle {\begin{aligned}\operatorname {Gi} (x)&{}=\operatorname {Bi} (x)\int _{x}^{\infty }\operatorname {Ai} (t)\,dt+\operatorname {Ai} (x)\int _{0}^{x}\operatorname {Bi} (t)\,dt,\\\operatorname {Hi} (x)&{}=\operatorname {Bi} (x)\int _{-\infty }^{x}\operatorname {Ai} (t)\,dt-\operatorname {Ai} (x)\int _{-\infty }^{x}\operatorname {Bi} (t)\,dt.\end{aligned}}}
エアリー関数 Ai( x )の定義を用いると、そのフーリエ変換は 次のように表せることが容易に分かる。これは、エアリー方程式のフーリエ変換を行うことで得られる。とおくと、 となり、解が存在する。フーリエ変換ではy が 十分速くゼロに減衰する必要があるため、解は1次元しかない。Biは 指数関数的に速く無限大に増加するため、フーリエ変換では得ることができない。 F ( Ai ) ( k ) := ∫ − ∞ ∞ Ai ( x ) e − 2 π i k x d x = e i 3 ( 2 π k ) 3 . {\displaystyle {\mathcal {F}}(\operatorname {Ai} )(k):=\int _{-\infty }^{\infty }\operatorname {Ai} (x)\ e^{-2\pi ikx}\,dx=e^{{\frac {i}{3}}(2\pi k)^{3}}.} y ^ = 1 2 π i ∫ y e − i k x d x {\textstyle {\hat {y}}={\frac {1}{2\pi i}}\int ye^{-ikx}dx} i y ^ ′ + k 2 y ^ = 0 {\displaystyle i{\hat {y}}'+k^{2}{\hat {y}}=0} y ^ = C e i k 3 / 3 . {\displaystyle {\hat {y}}=Ce^{ik^{3}/3}.}
アプリケーション
量子力学 エアリー関数は、三角形のポテンシャル井戸 内に閉じ込められた粒子、および一次元定数力場内の粒子に対する、時間に依存しないシュレーディンガー方程式の解である。同じ理由から、エアリー関数は、 WKB近似 の転換点付近において、ポテンシャルが局所的に位置の線形関数で近似できる場合に、一様な半古典的近似を与えるのにも役立つ。三角形のポテンシャル井戸解は、半導体 ヘテロ接合 に閉じ込められた電子の理解に直接関連している。
光学 横方向に非対称な光ビーム(電場 プロファイルがエアリー関数で与えられる)は、その最大強度が対称ビームの場合のように直線的に伝播するのではなく、片側に向かって加速する という興味深い特性を持つ。これは、低強度の裾野が反対方向に広がることを犠牲にしているため、ビーム全体の運動量は当然ながら保存される。
コースティクス エアリー関数は、虹 (いわゆる過剰虹)のような、光の方向性を持つ火面近傍の強度分布の形状を規定する。歴史的に、この数学的問題がエアリーにこの特殊な関数の開発を促した。1841年、 ウィリアム・ハロウズ・ミラーは、 薄い水筒に光を当て、望遠鏡で観測することで、過剰虹に類似した現象を実験的に測定した。彼は最大30本の帯状の虹を観測した。[ 9 ]
確率 1980年代半ばに、エアリー関数はチェルノフ分布 と密接に関係していることが判明しました。[ 10 ]
エアリー関数は、ランダム行列 における最大固有値の法則を記述するトレーシー・ウィドム分布 の定義にも現れる。ランダム行列理論とカルダー・パリシ・チャン方程式 は密接に関連しているため、KPZではエアリー過程 などの中心過程が構築されている。[ 11 ]
歴史 エアリー関数は、イギリスの天文学者で物理学者のジョージ・ビデル・エアリー (1801–1892)にちなんで名付けられました。彼は物理学における光学 の研究初期にこの関数に出会いました。[ 12 ] Ai( x )という表記法はハロルド・ジェフリーズ によって導入されました。エアリーは1835年に英国王立天文官 に就任し、1881年に引退するまでその職を務めました。
参照
注記 ^ Aspnes, David E. (1966). 「固体の閾値近傍における光吸収に対する電場効果」. Physical Review . 147 (2): 554– 566. doi : 10.1103/PhysRev.147.554 . ISSN 0031-899X . ^ 「エアリー関数と関連関数」 dlmf.nist.gov . 2022年 10月9日 閲覧 。 ^ a b Abramowitz & Stegun (1983 , p. 448)、式 10.4.59、10.4.61^ 「DLMF: §9.7 漸近展開 ‣ エアリー関数 ‣ 第9章 エアリー関数と関連関数」 dlmf.nist.gov . 2023年5月11日 閲覧 。 ^ a b c d Abramowitz & Stegun (1983 , p. 448)、式 10.4.60 および 10.4.64^ アブラモウィッツ、ミルトン 、 ステガン 、アイリーン・アン編 (1983) [1964年6月]。 「第10章」 。 『数式、グラフ、数表付き数学関数ハンドブック』 。応用数学シリーズ。第55巻(1972年12月発行の第10刷に訂正を加えた第9刷、初版)。ワシントンD.C.、ニューヨーク:米国商務省、国立標準局、ドーバー出版。448ページ 。ISBN 978-0-486-61272-0 LCCN 64-60036 . MR 0167642 . LCCN 65-12253 .^ Frank_William_John_Olver (1974).漸近論と特殊関数、 第11章. アカデミックプレス、ニューヨーク。^ M.Kh.Khokonov. ハード光子の放出によるエネルギー損失のカスケードプロセス // JETP, V.99, No.4, pp. 690-707 \ (2004). ^ ウィリアム・ハロウズ・ミラー「偽りの虹について」ケンブリッジ哲学協会紀要 7(1848年):277。 ^ Groeneboom, Piet; Lalley, Steven; Temme, Nico (2015). 「チェルノフ分布と放物型およびエアリー型の微分方程式」 . Journal of Mathematical Analysis and Applications . 423 (2): 1804– 1824. arXiv : 1305.6053 . doi : 10.1016/j.jmaa.2014.10.051 . S2CID 119173815 . ^ クアステル, ジェレミー; レメニック, ダニエル (2014). 「エアリー過程と変分問題」 . 浸透系と無秩序系の話題 . シュプリンガー数学・統計学会誌. 第69巻. pp. 121– 171. arXiv : 1301.0750 . doi : 10.1007/978-1-4939-0339-9_5 . ISBN 978-1-4939-0338-2 S2CID 118241762 .^ Airy (1838)、 「腐食性物質近傍における光の強度について」 、 ケンブリッジ哲学協会紀要 、 6 、大学出版局: 379–402 、 Bibcode : 1838TCaPS...6..379A
参考文献
外部リンク 



























![{\displaystyle \operatorname {Bi} (x)={\frac {1}{\pi }}\int _{0}^{\infty }\left[\exp \left(-{\tfrac {t^{3}}{3}}+xt\right)+\sin \left({\tfrac {t^{3}}{3}}+xt\right)\,\right]dt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3bcd1d018bad9c90fe2a8575dbb9038f2371ad4)


![{\displaystyle \operatorname {Ai} (z)\sim {\dfrac {1}{2{\sqrt {\pi }}\,z^{1/4}}}\exp \left(-{\frac {2}{3}}z^{3/2}\right)\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\,\Gamma \!\left(n+{\frac {5}{6}}\right)\,\Gamma \!\left(n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{n}}{2\pi \,n!\,z^{3n/2}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f5126841f2fbb258f59ecbe9253278655d74125)
![{\displaystyle \operatorname {Ai} (z)\sim {\dfrac {e^{-\zeta }}{4\pi ^{3/2}\,z^{1/4}}}\left[\sum _{n=0}^{\infty }{\dfrac {\Gamma \!\left(n+{\frac {5}{6}}\right)\,\Gamma \!\left(n+{\frac {1}{6}}\right)}{n!(-2\zeta )^{n}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6e3b873174de875bd4cbfc6622690a758c89585)


![{\displaystyle \operatorname {Bi} (z)\sim {\frac {1}{{\sqrt {\pi }}\,z^{1/4}}}\exp \left({\frac {2}{3}}z^{3/2}\right)\left[\sum _{n=0}^{\infty }{\dfrac {\Gamma \!\left(n+{\frac {5}{6}}\right)\,\Gamma \!\left(n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{n}}{2\pi \,n!\,z^{3n/2}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f26147bd014818b2de921af74ce2cb12329ebf4)
![{\displaystyle {\begin{aligned}\operatorname {Ai} (-z)\sim &{}\ {\frac {1}{{\sqrt {\pi }}\,z^{1/4}}}\sin \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {5}{6}}\right)\,\Gamma \!\left(2n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{2n}}{2\pi \,(2n)!\,z^{3n}}}\right]\\[6pt]&{}-{\frac {1}{{\sqrt {\pi }}\,z^{1/4}}}\cos \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {11}{6}}\right)\,\Gamma \!\left(2n+{\frac {7}{6}}\right)\left({\frac {3}{4}}\right)^{2n+1}}{2\pi \,(2n+1)!\,z^{3n\,+\,3/2}}}\right]\\[6pt]\operatorname {Bi} (-z)\sim &{}{\frac {1}{{\sqrt {\pi }}\,z^{1/4}}}\cos \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {5}{6}}\right)\,\Gamma \!\left(2n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{2n}}{2\pi \,(2n)!\,z^{3n}}}\right]\\[6pt]&{}+{\frac {1}{{\sqrt {\pi }}\,z^{\frac {1}{4}}}}\sin \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {11}{6}}\right)\,\Gamma \!\left(2n+{\frac {7}{6}}\right)\left({\frac {3}{4}}\right)^{2n+1}}{2\pi \,(2n+1)!\,z^{3n\,+\,3/2}}}\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e196759543503a1086e6fc8d6171705f1d358896)
![{\displaystyle \operatorname {Ai} '(z)\sim -{\dfrac {z^{1/4}}{2{\sqrt {\pi }}\,}}\exp \left(-{\frac {2}{3}}z^{3/2}\right)\left[\sum _{n=0}^{\infty }{\frac {1+6n}{1-6n}}{\dfrac {(-1)^{n}\,\Gamma \!\left(n+{\frac {5}{6}}\right)\,\Gamma \!\left(n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{n}}{2\pi \,n!\,z^{3n/2}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caed579ee27f7b2c095a7af0851c5c87c2034125)
![{\displaystyle \operatorname {Bi} '(z)\sim {\frac {z^{1/4}}{{\sqrt {\pi }}\,}}\exp \left({\frac {2}{3}}z^{3/2}\right)\left[\sum _{n=0}^{\infty }{\frac {1+6n}{1-6n}}{\dfrac {\Gamma \!\left(n+{\frac {5}{6}}\right)\,\Gamma \!\left(n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{n}}{2\pi \,n!\,z^{3n/2}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3794afa5aebc6c8b40f248ad361a1f931ad48d56)
![{\displaystyle {\begin{aligned}\operatorname {Ai} '(-z)\sim &{}-{\frac {z^{1/4}}{{\sqrt {\pi }}\,}}\cos \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\frac {1+12n}{1-12n}}{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {5}{6}}\right)\,\Gamma \!\left(2n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{2n}}{2\pi \,(2n)!\,z^{3n}}}\right]\\[6pt]&{}-{\frac {z^{1/4}}{{\sqrt {\pi }}\,}}\sin \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\frac {7+12n}{-5-12n}}{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {11}{6}}\right)\,\Gamma \!\left(2n+{\frac {7}{6}}\right)\left({\frac {3}{4}}\right)^{2n+1}}{2\pi \,(2n+1)!\,z^{3n\,+\,3/2}}}\right]\\[6pt]\operatorname {Bi} '(-z)\sim &{}\ {\frac {z^{1/4}}{{\sqrt {\pi }}\,}}\sin \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\frac {1+12n}{1-12n}}{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {5}{6}}\right)\,\Gamma \!\left(2n+{\frac {1}{6}}\right)\left({\frac {3}{4}}\right)^{2n}}{2\pi \,(2n)!\,z^{3n}}}\right]\\[6pt]&{}-{\frac {z^{1/4}}{{\sqrt {\pi }}\,}}\cos \left({\frac {2}{3}}z^{3/2}+{\frac {\pi }{4}}\right)\left[\sum _{n=0}^{\infty }{\frac {7+12n}{-5-12n}}{\dfrac {(-1)^{n}\,\Gamma \!\left(2n+{\frac {11}{6}}\right)\,\Gamma \!\left(2n+{\frac {7}{6}}\right)\left({\frac {3}{4}}\right)^{2n+1}}{2\pi \,(2n+1)!\,z^{3n\,+\,3/2}}}\right]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d79b5e8a69688ba7dce12b0eceec1c92fc1407c1)




![{\displaystyle \Re \left[\operatorname {Ai} (x+iy)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92d14f4ea89c98289bdd7724aa97a65bc37be26c)
![{\displaystyle \Im \left[\operatorname {Ai} (x+iy)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f188455d8f10f38330bed9927837e68fdbc9df46)

![{\displaystyle \operatorname {arg} \left[\operatorname {Ai} (x+iy)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2722a1be5b008fee5231676bfbecc9a6a15f6da)
![{\displaystyle \Re \left[\operatorname {Bi} (x+iy)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a2dd29c05abcff762111d663f165d7c1055d3de)
![{\displaystyle \Im \left[\operatorname {Bi} (x+iy)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/456ed57b8b06b7da31229c0cb6989b24c2d9b3d8)

![{\displaystyle \operatorname {arg} \left[\operatorname {Bi} (x+iy)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef422f3f85b66c485cf5b87ffa8b57b1b3e254a1)
![{\displaystyle {\begin{aligned}\operatorname {Ai} (x)&{}={\frac {1}{\pi }}{\sqrt {\frac {x}{3}}}\,K_{1/3}\!\left({\frac {2}{3}}x^{3/2}\right),\\\operatorname {Bi} (x)&{}={\sqrt {\frac {x}{3}}}\left[I_{1/3}\!\left({\frac {2}{3}}x^{3/2}\right)+I_{-1/3}\!\left({\frac {2}{3}}x^{3/2}\right)\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e861d86904629a2d1d12a7ce85411999080f2eb)


![{\displaystyle {\begin{aligned}\operatorname {Ai} (-x)&{}={\sqrt {\frac {x}{9}}}\left[J_{1/3}\!\left({\frac {2}{3}}x^{3/2}\right)+J_{-1/3}\!\left({\frac {2}{3}}x^{3/2}\right)\right],\\\operatorname {Bi} (-x)&{}={\sqrt {\frac {x}{3}}}\left[J_{-1/3}\!\left({\frac {2}{3}}x^{3/2}\right)-J_{1/3}\!\left({\frac {2}{3}}x^{3/2}\right)\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ecb62168bcf5ece20eaff8fe6f769991c1a63e4)





