ビット演算

コンピュータプログラミング において、ビット演算はビット列、ビット配列、または2進数値（ビット列とみなされる）を個々のビット単位で演算します。これは高速かつ単純な動作であり、高水準算術演算の基本であり、プロセッサによって直接サポートされています。ほとんどのアーキテクチャでは、2つのオペランドを持つ命令として提供される高価値ビット演算がいくつか提供されており、その結果は入力オペランドの1つを置き換えます。

シンプルで低コストなプロセッサでは、通常、ビット演算は除算よりも大幅に高速で、乗算よりも数倍高速であり、場合によっては加算よりも大幅に高速です。現代のプロセッサは、命令パイプラインの長さやその他のアーキテクチャ設計上の選択により、加算と乗算をビット演算と同程度の速度で実行することが一般的ですが、ビット演算はリソースの使用量が減少するため、一般的に消費電力が少なくなります。^{[ 1 ]}

ビット演算子

以下の説明では、ビットの位置を示す場合は、右（最下位）側から左へ進んで数えます。例えば、2進値0001（10進数では1）は、最初の位置（つまり右端）を除くすべての位置に0が存在します。

ない

ビット否定（またはビット補数）は、各ビットの論理否定を行い、与えられた2進値の1の補数を生成する単項演算です。0のビットは1になり、1のビットは0になります。例：

0 111ではない(10進数の 7) = 1 000（10進数8） 

10101011ではない（10進数171） = 01010100 (10進数では84) 

結果は、値から1を引いた値の2の補数に等しくなります。2の補数演算を使用する場合は、次のようになりますNOT x = -x − 1。

符号なし整数の場合、数値のビットごとの補数は、符号なし整数の範囲の中間点を挟んで数値を「鏡映反転」したものです。例えば、8ビットの符号なし整数 の場合、NOT x = 255 - xこれはグラフ上で下向きの線として視覚化でき、0から255までの増加範囲を、255から0まで減少する範囲に実質的に「反転」します。単純ですが分かりやすい使用例として、各ピクセルが符号なし整数として保存されている グレースケール画像を反転することが挙げられます。

そして

4ビット整数のビット単位のAND

ビットANDは、2つの等長バイナリ表現を受け取り、対応するビットの各ペアに対して論理積演算を実行するバイナリ演算です。したがって、比較位置のビットが両方とも1の場合、結果のバイナリ表現のビットは1（1 × 1 = 1）になります。それ以外の場合、結果は0（1 × 0 = 0、0 × 0 = 0）になります。例えば、次のようになります。

 010 1（10進数5） AND 001 1 (10進数3) = 000 1 (10進数の1) 

この演算は、特定のビットがセット（1）されているかクリア（0）されているかを判断するために使用できます。例えば、ビットパターン0011（10進数で3）が与えられた場合、2番目のビットがセットされているかどうかを判断するには、2番目のビットのみに1を含むビットパターンとのビット単位のAND演算を使用します。

 00 1 1（10進数3） AND 00 1 0 (10進数2) = 00 1 0 (10進数2) 

結果の0010は非ゼロなので、元のパターンの2番目のビットがセットされていることがわかります。これはしばしばビットマスキングと呼ばれます。（例え話で言えば、マスキングテープは変更すべきでない部分、あるいは重要でない部分を覆い隠す、つまりマスクするものです。この場合、0の値は重要でないビットをマスクします。）

ビットAND演算は、各ビットが個別のブール値を表すレジスタの選択されたビット（またはフラグ）をクリアするために使用できます。この手法は、可能な限り少ないメモリを使用して、多数のブール値を格納する効率的な方法です。

例えば、0110（10進数で6）は、右から左に番号が付けられた4つのフラグのセットと考えることができます。1番目と4番目のフラグはクリア（0）、2番目と3番目のフラグはセット（1）です。3番目のフラグは、3番目のビットのみに0が含まれるパターンとのビット単位のAND演算によってクリアできます。

 0 1 10（10進数6） AND 1 0 11（10進数の11） = 0 0 10 (10進数2) 

この特性により、最下位ビットの値をチェックすることで、2進数の パリティチェックが容易になります。上記の例を用いると、

 011 0（10進数6） AND 000 1（10進数の1） = 000 0 (10進数の0) 

6 AND 1 は 0 なので、6 は 2 で割り切れ、したがって偶数です。

または

4ビット整数のビットごとのOR

ビット論理和は、同じ長さの2つのビットパターンを取り、対応するビットのペアごとに論理和をとる二項演算です。両方のビットが0の場合、各位置の結果は0になり、それ以外の場合は1になります。例えば、

 0 101（10進数5） または 0 011 (10進数3) = 0 111 (10進数の7) 

ビット単位のOR演算は、上記のレジスタの選択されたビットを1に設定するために使用できます。例えば、0010（10進数で2）の4番目のビットは、4番目のビットのみをセットしたパターンとビット単位のOR演算を行うことで設定できます。

0 0 1 0 （10進数の2） または1 0 0 0 (10進数8) = 1 0 1 0 （10進数の10） 

排他的論理和

4ビット整数のビット単位のXOR

ビット単位のXOR演算は、同じ長さの2つのビットパターンを受け取り、対応するビットのペアごとに排他的論理和演算を実行する二項演算です。各位置の結果は、片方のビットだけが1の場合は1、両方が0または両方が1の場合は0になります。この演算では、2つのビットを比較し、2つのビットが異なる場合は1、同じ場合は0になります。例えば、

 0 10 1（10進数の5） XOR 0 01 1 (10進数3) = 0 11 0 (10進数6) 

ビット単位のXOR演算は、レジスタ内の選択されたビットを反転（トグルまたはフリップとも呼ばれます）するために使用できます。任意のビットを1とXOR演算することでトグルできます。例えば、ビットパターン0010（10進数で2）の場合、2番目と4番目のビットは、2番目と4番目の位置に1を含むビットパターンとのビット単位のXOR演算によってトグルできます。

0 0 1 0 （10進数の2） XOR 1 0 1 0 (10進数10) = 1 0 0 0 (10進数の8) 

この技術は、ブール状態のセットを表すビット パターンを操作するために使用できます。

アセンブリ言語プログラマや最適化コンパイラは、レジスタの値をゼロに設定するためのショートカットとして、XOR演算を使用することがあります。ある値とそれ自身とのXOR演算は常にゼロになり、多くのアーキテクチャでは、この演算はゼロ値をロードしてレジスタに保存するよりもクロックサイクルとメモリ消費量が少なくて済みます。

固定長nのビット文字列の集合(つまりマシンワード) を体 上のn次元ベクトル空間 と考えると、ベクトルの加算はビット単位の XOR に対応します。 ${\displaystyle {\bf {F}}_{2}^{n}}$ ${\displaystyle {\bf {F}}_{2}}$

数学的等価性

⁠ ⁠${\displaystyle x\geq y}$ と仮定すると、非負の整数の場合、ビット演算は次のように記述できます。

${\displaystyle {\begin{aligned}\operatorname {NOT} (x)&=\sum _{n=0}^{\lfloor \log _{2}x\rfloor }2^{n}\left(\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}+1\right){\bmod {2}}\right)\\&=\left(2^{\lfloor \log _{2}x\rfloor +1}-1\right)-x\\[10pt]x\operatorname {AND} y&=\sum _{n=0}^{\lfloor \log _{2}x\rfloor }2^{n}\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right)\\[10pt]x\operatorname {OR} y&=\sum _{n=0}^{\lfloor \log _{2}x\rfloor }2^{n}{\Bigg (}\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}+\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\\&\qquad \qquad -\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right){\Bigg )}\\[10pt]x\operatorname {XOR} y&=\sum _{n=0}^{\lfloor \log _{2}x\rfloor }2^{n}\left(\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor +\left\lfloor {\frac {y}{2^{n}}}\right\rfloor \right){\bmod {2}}\right)\end{aligned}}}$

すべての二項論理演算子の真理値表

2つの2値変数には16通りの真理値関数があり、これはLUT2ルックアップテーブルと呼ばれる真理値表、つまりブール関数の順序k=2（2入力）を定義します。ベンダーによっては、特定の2値連結子を識別する4ビットフィールドを持つ命令を「連結子」^{[ 2 ]}と呼び、16通りの異なるオペコードを「ブール演算」^{[ 3 ]}と呼ぶ場合もあります。

以下は 2 つのビット P と Q のビット単位の等価演算です。

p	q		F ^0	NOR ^1	Xq ^2	^3ページ	↛ ^4	¬q^5	排他的論理和^6	NAND ^7		そして^8	XNOR ^9	問^10	もし/ならば^11	^12ページ	^13の場合	または^14	T ^15
1	1		0	0	0	0	0	0	0	0		1	1	1	1	1	1	1	1
1	0		0	0	0	0	1	1	1	1		0	0	0	0	1	1	1	1
0	1		0	0	1	1	0	0	1	1		0	0	1	1	0	0	1	1
0	0		0	1	0	1	0	1	0	1		0	1	0	1	0	1	0	1
ビット単位の等価性			0	NOT (p または q)	(pではない)かつ q	pではない	p かつ(q ではない)	いいえ​	p 排他的論理和 q	(p かつ q)ではない		p と q	NOT (p XOR q)	q	(pではない)または q	p	p または(q ではない)	p または q	1

3 進法で同等のものは、順序 k = 3 (3 つの入力) の LUT3ブール関数であり、結果として 256 の演算のテーブルが生成され、コンピューティングではビット単位の 3 進法論理命令と呼ばれます。

ビットシフト

ビットシフトは、値を数値ではなくビット列として扱うため、ビット単位の演算と見なされることがあります。これらの演算では、桁が左または右に移動（シフト）されます。コンピュータプロセッサのレジスタは固定幅であるため、レジスタの一方の端では一部のビットが「シフトアウト」され、もう一方の端では同じ数のビットが「シフトイン」されます。ビットシフト演算子間の違いは、シフトインされるビットの値をどのように決定するかにあります。

ビットアドレス指定

レジスタの幅（多くの場合32ビット、あるいは64ビット）が、アドレス指定可能な最小単位（バイトと呼ばれることが多い）のビット数（通常は8ビット）よりも大きい場合、シフト演算はバイトからビットへのアドレス指定方式を誘導します。この場合、「左」と「右」の方向は、位取り記法における数値の標準的な表記法から採用されます。つまり、左シフトは数値の値を増加させ、右シフトは数値を減少させます。つまり、左の桁を先に読み取る場合、ビッグエンディアン方式となります。レジスタの両端における境界効果を無視すると、算術シフト演算と論理シフト演算は同じ動作をし、8ビットシフトはビットパターンを1バイト分、次のように転送します。

リトルエンディアン順序:	8桁左シフトするとバイトアドレスが1増加します。
	8 位置右シフトすると、バイト アドレスが 1 減少します。
ビッグエンディアン順序:	8桁左シフトするとバイトアドレスは1減少します。
	8 位置右シフトすると、バイト アドレスが 1 増加します。

算術シフト

左算術シフト

右算術シフト

算術シフト（スティッキーシフト）では、両端からシフトアウトされたビットは破棄されます。左算術シフトでは、右側にゼロがシフトインされます。右算術シフトでは、符号ビット（2の補数におけるMSB）が左側にシフトインされるため、オペランドの符号は保持されます。

この例では、2 の補数として解釈される 8 ビット レジスタを使用します。

 00010111 (10進数 +23) 左シフト = 0010111 0 (10進数 +46) 

 10010111 (10進数 -105) 右シフト = 1 1001011 (10進数 -53) 

最初のケースでは、左端の桁がレジスタの末尾を超えてシフトされ、右端に新たな0がシフトされました。2番目のケースでは、右端の1がシフトアウトされ（おそらくキャリーフラグに）、符号を保持したまま左端に新たな1がコピーされました。複数のシフトは、ある桁数分の1回のシフトに短縮されることがあります。例えば、

 00010111 (10進数 +23) 左シフト2 = 010111 00 (10進数 +92) 

nの左算術シフトは2 ⁿを掛けることと等価です（ただし、値がオーバーフローしない場合）。一方、2の補数値のnの右算術シフトは、 2 ⁿによる除算の切り捨て値を取ることと等価です。2進数を1の補数として扱う場合、同じ右シフト演算は 2 ⁿによる除算となり、ゼロに向かって丸められます。

論理的変化

左論理シフト

右論理シフト

論理シフト（ゼロフィルシフト）では、破棄されたビットをゼロで置き換えます。したがって、論理シフトと算術シフトの左シフトはまったく同じです。

ただし、論理右シフトは、符号ビットをコピーする代わりに、最上位ビットに値 0 ビットを挿入するため、符号なしの 2 進数には最適ですが、算術右シフトは、符号付きの2 の補数 2進数には最適です。

循環シフト

シフトの別の形式は、循環シフト、ビット回転、またはビット回転です。

回転

左に円形シフトまたは回転

右回転またはシフト

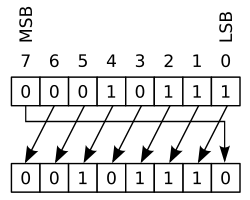この操作は「ローテート・ノー・キャリー」とも呼ばれ、レジスタの左端と右端が結合されたかのようにビットが「回転」します。左シフト操作で右にシフトされる値は、左シフトでシフトアウトされた値と同じであり、右シフト操作ではその逆になります。これは、既存のビットをすべて保持する必要がある場合に便利であり、デジタル暗号化で頻繁に使用されます。

キャリーを通して回転する

左回転でキャリー

右回転でキャリー

キャリーによる回転は回転操作の変形であり、シフトインされるビット (どちらかの端) はキャリー フラグの古い値になり、シフトアウトされるビット (もう一方の端) はキャリー フラグの新しい値になります。

キャリーフラグを事前に設定することで、単一の回転（キャリー経由）命令は、x RIGHT-ROTATE-THROUGH-CARRY-BY-ONE 1桁の論理シフトまたは算術シフトをシミュレートできます。例えば、キャリーフラグに0が格納されている場合、は論理右シフト、キャリーフラグに符号ビットのコピーが格納されている場合、はx RIGHT-ROTATE-THROUGH-CARRY-BY-ONE算術右シフトです。このため、ローエンドのPICなどの一部のマイクロコントローラでは、回転命令と回転（キャリー経由）命令のみを備え、算術シフト命令や論理シフト命令は使用しません。

回転キャリーは、プロセッサのネイティブワードサイズよりも大きな数値のシフトを実行する場合に特に便利です。これは、大きな数値が2つのレジスタに格納されている場合、最初のレジスタの一方の端からシフトされたビットは、2番目のレジスタのもう一方の端から入力される必要があるためです。回転キャリーでは、そのビットは最初のシフト中にキャリーフラグに「保存」され、追加の準備なしに2番目のシフトでシフトインする準備が整います。

高級言語では

C言語ファミリー

C言語およびC++言語では、論理シフト演算子は<<左シフトの場合は「 」、>>右シフトの場合は「 」です。シフトする桁数は、演算子の2番目の引数で指定します。例えば、

x = y << 2 ;

2 ビット左に xシフトした結果を割り当てます。これは 4 倍の乗算に相当します。y

シフトは実装定義の動作または未定義の動作を引き起こす可能性があるため、使用時には注意が必要です。ワードサイズ以上のビット数でシフトした結果は、CおよびC++では未定義の動作となります。^{[ 4 ] [ 5 ]}負の値を右シフトすることは実装定義であり、良いコーディングプラクティスでは推奨されません。^{[ 6 ]}符号付き値を左シフトした結果が結果型で表現できない場合、結果は未定義となります。^{[ 4 ]}

C#では、最初のオペランドがint型またはlong型の場合、右シフトは算術シフトです。最初のオペランドがuint型またはulong型の場合、右シフトは論理シフトです。^{[ 7 ]}

循環シフト

C言語ファミリーには回転演算子がない（C++20では と が提供されているがstd::rotl）が、シフト演算子から合成することができる。セキュリティ要件のあるソフトウェアでは、未定義の動作やタイミング攻撃をstd::rotr回避するために、文が適切に構成されていることを確認する必要がある。^{[ 8 ]}例えば、32ビットの符号なし値を位置で左回転させる単純な実装は、単に xn

uint32_t x = ..., n = ...; uint32_t y = ( x << n ) | ( x >> ( 32 - n ));

しかし、0ビットシフトを行うと、右辺の式は未定義の動作になります。(x >> (32 - n))なぜなら、32 - 0は であり、は0～31の範囲外だからです。2回目の試行では、 3232

uint32_t x = ..., n = ...; uint32_t y = n ? ( x << n ) | ( x >> ( 32 - n )) : x ;

シフト量が未定義の動作を招かないことを確認するためにテストされます。しかし、この分岐によってコードパスが追加され、タイミング解析や攻撃の機会が生じます。これは、高信頼性ソフトウェアでは許容されないことがよくあります。^{[ 8 ]}さらに、コードは複数の機械語命令にコンパイルされるため、プロセッサのネイティブ命令よりも効率が悪くなることがよくあります。

GCCおよびClangにおける未定義動作と分岐を回避するには、以下の方法が推奨されます。このパターンは多くのコンパイラで認識され、コンパイラは単一の回転命令を生成します。^{[ 9 ] [ 10 ] [ 11 ]}

uint32_t x = ..., n = ...; uint32_t y = ( x << n ) | ( x >> ( - n & 31 ));

Microsoft Visual C++の_rotl8、_rotl16、_rotr8、_rotr16のように、循環シフトを実装するコンパイラ固有の組み込み関数も存在します。ClangはMicrosoftとの互換性のために回転組み込み関数を提供していますが、上記の問題を抱えています。^{[ 11 ]} GCCは回転組み込み関数を提供していません。Intelもx86組み込み関数を提供しています。

ジャワ

Java では、すべての整数型は符号付きであるため、「<<」演算子と「>>」演算子は算術シフトを実行します。Javaでは論理右シフトを実行するために「 」演算子が追加されていますが、符号付き整数の場合、論理左シフトと算術左シフトの演算は同じであるため、 Javaには「 」演算子は >>>ありません。<<<

Javaシフト演算子の詳細: ^{[ 12 ]}

• 演算子<<(左シフト)、>>(符号付き右シフト)、 (符号なし右シフト) はシフト演算子>>>と呼ばれます。
• シフト式の型は、左辺のオペランドの型を昇格したものになります。例えば、aByte >>> 2は と同等です。((int)aByte)>>>2
• 左辺オペランドの昇格型がint型の場合、右辺オペランドの下位5ビットのみがシフト量として使用されます。これは、右辺オペランドにマスク値0x1f（0b11111）を持つビット単位の論理積演算子「&」を適用した場合と同等です。^{[ 13 ]}したがって、実際に使用されるシフト量は常に0から31までの範囲となります。
• 左辺オペランドの昇格型がlong型の場合、右辺オペランドの下位6ビットのみがシフト量として使用されます。これは、右辺オペランドにマスク値0x3f（0b111111）を持つビット単位の論理積演算子「&」を適用した場合と同等です。^{[ 13 ]}したがって、実際に使用されるシフト量は常に0から63までの範囲となります。
• の値は、ゼロ拡張を使用してn右シフトされたsn >>> sビット位置です。
• ビット演算およびシフト演算では、型はbyte暗黙的に に変換されますint。バイト値が負の場合、最上位ビットは 1 となり、int の余分なバイトを埋めるために 1 が使用されます。したがって、結果は になります。byteb1=-5;inti=b1|0x0200;i == -5

JavaScript

JavaScriptはビット演算を使用して、2つ以上の単位のそれぞれを1または0に評価します。 ^{[ 14 ]}

パスカル

Pascal およびそのすべての方言（Object PascalやStandard Pascalなど）では、論理左シフト演算子と論理右シフト演算子はそれぞれ " shl" と " shr" です。符号付き整数の場合でも、shr論理シフトのように動作し、符号ビットはコピーされません。シフトする桁数は2番目の引数で指定します。例えば、次のコードはy を2ビット左に シフトした結果をx に代入します。

x := y shl 2 ;

他の

• 暗号で使用されるポップカウント
• 先頭のゼロを数える
• 2進化10進数

アプリケーション

ビット演算は、デバイス ドライバー、低レベル グラフィックス、通信プロトコル パケットのアセンブリ、デコード などの低レベル プログラミングでは特に必要です。

マシンには算術演算や論理演算を実行するための効率的な組み込み命令が備わっていることが多いが、これらの演算はすべて、ビット演算子とゼロテストをさまざまな方法で組み合わせることで実行できる。^{[ 15 ]} たとえば、次の図は、ビットシフトと加算のみを使用して、任意の2つの整数と（より大きい） を乗算する方法を示す古代エジプトの乗算の擬似コード実装である。abab

c ← 0 while b ≠ 0 if ( b and 1 ) ≠ 0 c ← c + a aを1左シフトbを1右シフトcを返す

もう 1 つの例は、ビット演算子とゼロ テストを使用して 2 つの整数の合計を計算する方法を示す、加算の擬似コード実装ですa。b

a ≠ 0の場合c ← bかつa b ← b xor aを左シフトcを1 だけシフトa ← c bを返す

ブール代数

ビット演算で構成される複雑な式を簡略化すると便利な場合があります。例えば、コンパイラを作成する場合などです。コンパイラの目的は、高水準プログラミング言語を可能な限り効率的な機械語に変換することです。ブール代数は、複雑なビット演算式を簡略化するために使用されます。

そして

• x & y = y & x
• x & (y & z) = (x & y) & z
• x & 0xFFFF = x^{[ 16 ]}
• x & 0 = 0

• x & x = x

または

• x | y = y | x
• x | (y | z) = (x | y) | z
• x | 0 = x
• x | 0xFFFF = 0xFFFF
• x | x = x

ない

• ~(~x) = x

排他的論理和

• x ^ y = y ^ x
• x ^ (y ^ z) = (x ^ y) ^ z
• x ^ 0 = x
• x ^ y ^ y = x
• x ^ x = 0
• x ^ 0xFFFF = ~x

さらに、XORは3つの基本演算（AND、OR、NOT）を使用して構成できます。

• a ^ b = (a | b) & (~a | ~b)
• a ^ b = (a & ~b) | (~a & b)

その他

• x | (x & y) = x
• x & (x | y) = x
• ~(x | y) = ~x & ~y
• ~(x & y) = ~x | ~y
• x | (y & z) = (x | y) & (x | z)
• x & (y | z) = (x & y) | (x & z)
• x & (y ^ z) = (x & y) ^ (x & z)
• x + y = (x ^ y) + ((x & y) << 1)
• x - y = ~(~x + y)

逆関数と方程式の解法

ブール代数では、通常の代数とは異なり、いくつかの演算に逆元がないため、変数の解を求めるのが難しい場合があります。逆元がない演算は、実行時に元のデータビットの一部が失われ、この失われた情報を回復することはできません。

• 逆数を持つ
  • ない
  • 排他的論理和
  • 左に回転
  • 右に回転
• 逆はない
  • そして
  • または
  • 左にシフト
  • 右にシフト

演算順序

このリストの先頭にある操作が最初に実行されます。より完全なリストについては、メインの記事をご覧ください。

• ( )
• ~ -^{[ 17 ]}
• * / %
• + -^{[ 18 ]}
• << >>
• &
• ^
• |

参照

• 算術論理ユニット
• ビット操作
• ビットボード
• C言語におけるビット演算
• ダブルダブル
• 最初のセットを見つける
• カルノー図
• 論理ゲート
• 論理演算子
• プリミティブデータ型

参考文献

1. 「CMicrotek低消費電力設計ブログ」 . CMicrotek . 2015年8月12日閲覧。
2. 「Connective Operations」（PDF） .リファレンス・マニュアル - IBM 7030 データ処理システム（PDF） . IBM . 1961年8月 . pp.  74– 77. A22-6530-2 . 2015年5月5日閲覧– bitsavers.org経由。
3. 「算術および論理演算」（PDF） .プログラム型データプロセッサ6 - ハンドブック（PDF） . Digital Equipment Corporation . 1964年8月. p.  32. F-65 . 2015年5月5日閲覧– bitsavers.org経由.
4. JTC1/SC22/WG14 N843「Cプログラミング言語」、セクション6.5.7
5. 「算術演算子 - cppreference.com」 . en.cppreference.com . 2016年7月6日閲覧。
6. 「INT13-C. ビット演算子は符号なしオペランドにのみ使用する」 CERT : セキュアコーディング標準。カーネギーメロン大学ソフトウェア工学研究所。 2015年9月7日閲覧。
7. 「Operator (C# リファレンス)」 . Microsoft . 2013年7月14日閲覧。
8. 「標準に違反しないほぼ一定時間の回転？」 Stack Exchange Network . 2015年8月12日閲覧。
9. 「ポータブル回転イディオムの最適化が不十分」 GNU GCCプロジェクト。2015年8月11日閲覧。
10. 「C/C++標準に違反しない円形回転？」 Intel Developer Forums 。 2015年8月12日閲覧。
11. 「定数がインラインアセンブリに伝播されず、「制約 'I' には整数定数式が必要です」という結果になる」 LLVM プロジェクト. 2015年8月11日閲覧。
12. Java言語仕様、セクション15.19。シフト演算子
13. 「第15章 式」 . oracle.com .
14. 「JavaScript ビットワイズ」 W3Schools.com。
15. 「ビットシフトトリックを用いた算術演算の合成」 . Bisqwit.iki.fi. 2014年2月15日. 2014年3月8日閲覧。
16. この記事全体を通して、0xFFFF はデータ型のすべてのビットを 1 に設定する必要があることを意味します。正確なビット数はデータ型の幅によって異なります。
17. - はここでは減算ではなく否定です
18. - はここでは減算であり、否定ではない

外部リンク

• オンラインビット演算計算機はビットAND、OR、XORをサポートします
• XORcat、ビット単位の XOR ファイル/ストリーム用のツール
• ビットシフトを使った除算
• 「Bitwise Operations Mod N」、Enrique Zeleny、Wolfram Demonstrations Project 著。
• 「ビット演算の構成のプロット」、Enrique Zeleny、Wolfram デモンストレーション プロジェクト。