遠心圧縮機
遠心インペラ単体
ターボチャージャーの一部として示されている遠心圧縮機（青色）
遠心圧縮機（青色）は軸遠心ジェットエンジンの第2段として示されている。

遠心圧縮機は、インペラ圧縮機やラジアル圧縮機とも呼ばれ、動的な軸対称の仕事吸収型ターボ機械のサブクラスです。[ 1 ]

これらの装置は、ローター／インペラを通る流体の連続的な流れにエネルギーを加えることで圧力上昇を実現します。次のセクションの式は、このエネルギー入力の比を示しています。このエネルギーの大部分は運動エネルギーであり、ディフューザーを通る流れを減速させることで、位置エネルギー／静圧の増加に変換されます。インペラにおける静圧上昇は、ディフューザーにおける静圧上昇とほぼ等しくなります。

単純な遠心圧縮機のコンポーネント

図1.1 – 2段ターボシャフト、第1段流路、環状入口、ガイドベーン、オープンインペラ、ベーン付きディフューザ、ベーンレスリターンベンド

単純な遠心圧縮機段は、4つの部品（通過流の順に記載）から構成されています。入口、インペラ／ローター、ディフューザー、コレクターです。[ 1 ]図1.1は、流路の各部品を示しています。作動ガス（作動ガス）は、左から右へ軸方向に遠心インペラに流入します。このターボシャフト（またはターボプロップ）インペラは、圧縮機の下流側から見ると反時計回りに回転しています。流れは圧縮機を左から右へ通過します。

入口

遠心圧縮機への最もシンプルな入口は、通常、単純なパイプです。用途によっては、入口は非常に複雑になる場合があります。入口には、入口絞り弁、シュラウド付きポート、環状ダクト（図1.1参照）、分岐ダクト、流れを整流または旋回させるために使用される固定ガイドベーン/翼（図1.1参照）、可動ガイドベーン（プレスワールを調整するために使用）などのコンポーネントが含まれる場合があります。圧縮機の入口には、圧縮機の性能を制御するために、圧力と温度を測定するための計器が組み込まれていることがよくあります。

ベルヌーイの定理は、入口のような羽根のない固定部品を理解する上で重要な役割を果たします。工学的な状況では、断熱流れを仮定すると、この式は次のようになります。

どこ：

  • 下付き文字0はコンプレッサーの入口、ステーション0です
  • 下付き文字1はインペラの入口、ステーション1です
  • pは圧力
  • ρは密度であり、圧力の関数であることを示す。ρ（p〜）{\displaystyle \rho ({\tilde {p}})}
  • v{\displaystyle v}流速は
  • γは流体の比熱の比である

遠心羽根車

図1.2.1 – ターボチャージャーインペラに似たインペラのグラフィカルモデリング

遠心圧縮機段の識別部品は、遠心インペラローターです。インペラは、「オープン」（ブレードが見える）、「カバー付きまたはシュラウド付き」、「スプリッター付き」（インデューサを1枚おきに除去）、および「スプリッターなし」（すべてのブレードがフルブレード）など、様々な構成で設計されています。図1.1、1.2.1、および1.3は、フルブレード/ベーンと短いスプリッタブレード/ベーンを交互に配置した、3種類のオープン型フルインデューサローターを示しています。一般的に、数学的な命名法では、インペラの前縁を下付き文字1で表します。同様に、インペラの後縁を下付き文字2で表します。

作動ガス（流体）がインペラをステーション1からステーション2へと通過するにつれて、運動エネルギーと位置エネルギーが増加します。これは軸流圧縮機と全く同じですが、インペラの半径が大きくなるにつれてガスがより高いエネルギーレベルに達するという点が異なります。多くの現代の高効率遠心圧縮機では、インペラから排出されるガスは音速に近い速度で移動します。

現代の高効率インペラのほとんどは、ブレード形状に「バックスイープ」を採用しています。[ 2 ] [ 3 ] [ 4 ]

一般的なオイラー方程式から導出されるオイラーのポンプとタービンの方程式は、インペラの性能を理解する上で重要な役割を果たします。この方程式は次のように表すことができます。

  • 下付き文字1はインペラの前縁（入口）、ステーション1
  • 下付き文字2はインペラ後縁（排出口）、ステーション2
  • Eは流体に加えられるエネルギーである
  • gは重力加速度である
  • uはインペラの周速、単位は速度
  • wはインペラに対する流れの速度であり、単位は速度である。
  • cは静止状態に対する流れの絶対速度、単位速度
  • 図1.2.2 – 遠心圧縮機インペラの入口速度三角形
    図1.2.2 – 遠心圧縮機インペラの入口速度三角形
  • 図1.2.3 – 遠心圧縮機インペラの出口速度三角形
    図1.2.3 – 遠心圧縮機インペラの出口速度三角形

ディフューザー

図1.3 – NASA CC3インペラとウェッジディフューザー

単純な遠心圧縮機において、インペラの下流に位置する次の部品はディフューザーである。[ 5 ] [ 4 ]ディフューザーは、気体の速度を徐々に遅くする（拡散させる）ことで、流れの運動エネルギー（高速度）を位置エネルギー（静圧）の増加に変換する。ディフューザーには、羽根なし、羽根付き、またはそれらの組み合わせがある。高効率の羽根付きディフューザーは、1未満から4を超える広いソリディティ範囲で設計されている。羽根付きディフューザーのハイブリッド型には、ウェッジ型（図1.3を参照）、チャネル型、パイプ型がある。一部のターボチャージャーにはディフューザーがない。一般に受け入れられている命名法では、ディフューザーの前縁をステーション3、後縁をステーション4と呼ぶことがある。

ベルヌーイの定理は、ディフューザーの性能を理解する上で重要な役割を果たします。工学的な状況では、断熱流を仮定すると、この式は次のようになります。

どこ：

  • 添え字2はディフューザーの入口、ステーション2です
  • 下付き文字4はディフューザーの排出口、ステーション4です。
  • (上記の入口を参照してください。)

コレクタ

図1.4 – 遠心圧縮機の主要構成部品を示すモデル

遠心圧縮機のコレクターは様々な形状や形態をとることができます。[ 5 ] [ 4 ]ディフューザーが円周方向に一定面積を持つ大きな空洞のチャンバーに排気する場合、コレクターはプレナムと呼ばれることがあります。ディフューザーがカタツムリの殻、牛の角、またはフレンチホルンのような形状の装置に排気する場合、コレクターは渦巻き状またはスクロール状と呼ばれることが多いです。

ディフューザーが環状のベンドに排出する場合、コレクターは燃焼器入口（ジェットエンジンやガスタービンで使用）または戻り通路（オンライン多段圧縮機で使用）と呼ばれることがあります。その名前が示すように、コレクターの目的は、ディフューザーの排出環状部からの流れを集め、この流れを下流のアプリケーションに必要なコンポーネントに送り込むことです。コレクターまたは排出管には、圧縮機を制御するためのバルブや計器が組み込まれている場合もあります。アプリケーションによっては、コレクターはディフューザーよりもはるかに効率よく流れを拡散（運動エネルギーを静圧に変換）します。[ 6 ]

ベルヌーイの定理は、ディフューザーの性能を理解する上で重要です。工学的な状況では、断熱流を仮定すると、この式は次のようになります。

どこ：

  • 下付き文字4はディフューザーの入口、ステーション4です。
  • 下付き文字5はディフューザーの排出口、ステーション5です。
  • (上記の入口を参照してください。)

歴史的貢献、先駆者たち

過去100年間にわたり、Stodola (1903, 1927–1945)、[ 7 ] Pfleiderer (1952)、[ 8 ] Hawthorne (1964)、[ 9 ] Shepherd (1956) 、 [ 1 ] Lakshminarayana ( 1996 )、[ 10 ] Japikse (引用文献を含む多数の文献)、[ 2 ] [ 11 ] [ 12 ]といった応用科学者たちが、若い技術者にターボ機械の基礎を教えてきました。これらの知識は、軸流、斜流、遠心／遠心といった構成のあらゆる動的、連続流、軸対称ポンプ、ファン、ブロワー、コンプレッサーに当てはまります。

この関係こそが、タービンや軸流圧縮機の進歩が、遠心圧縮機を含む他のターボ機械にもしばしば応用される理由です。図2.1と2.2は、遠心圧縮機のラベルを付けてターボ機械の領域を示しています。[ 13 ] [ 14 ]遠心圧縮機の改良は、大規模な発見によって達成されたわけではありません。むしろ、多くの人々によって発見された漸進的な知識を理解し、応用することで達成されてきました。

空気力学・熱力学領域

図2.1 – ターボ機械の空力熱伝達領域

図2.1（右図）はターボ機械の空力熱領域を表している。横軸は熱力学第一法則から導かれるエネルギー方程式を表している。[ 1 ] [ 14 ]縦軸はマッハ数で特徴づけられ、流体の圧縮性（または弾性）の範囲を表している。[ 1 ] [ 14 ] Z軸はレイノルズ数で特徴づけられ、流体の粘性（または粘着性）の範囲を表している。[ 14 ]この気熱領域の基礎を確立した数学者と物理学者には、[ 15 ] [ 16 ]アイザック・ニュートン、ダニエル・ベルヌーイ、レオンハルト・オイラー、クロード＝ルイ・ナビエ、ジョージ・ストークス、エルンスト・マッハ、ニコライ・エゴロヴィチ・ジュコフスキー、マルティン・クッタ、ルートヴィヒ・プラントル、セオドア・フォン・カルマン、パウル・リヒャルト・ハインリヒ・ブラシウス、アンリ・コアンダなどがいます。

物理機械領域

図2.2 – ターボ機械の物理領域

図2.2（右図）は、ターボ機械の物理的、あるいは機械的な領域を表しています。ここでも、横軸はエネルギー方程式を表し、左側ではタービンが動力を発生し、右側ではコンプレッサーが動力を吸収します。[ 1 ] [ 14 ]物理的領域において、縦軸はターボ機械の用途に応じて高速と低速を区別します。[ 1 ] [ 14 ] Z軸は、ターボ機械の物理的領域において、軸流形状と放射状流形状を区別します。[ 1 ] [ 14 ]斜流ターボ機械は、軸流と放射状流の中間に位置すると考えられます。[ 1 ] [ 14 ]ターボ機械の実用化を推進した技術的成果の主な貢献者としては、[ 15 ] [ 16 ]デニス・パパン、[ 17 ]ケルネリエン・ル・デモール、ダニエル・ガブリエル・ファーレンハイト、ジョン・スミートン、ACE・ラトー博士、[ 18 ]ジョン・バーバー、アレクサンダー・サブルコフ、サー・チャールズ・アルジャーノン・パーソンズ、エギディウス・エリング、サンフォード・アレクサンダー・モス、ウィリス・キャリアー、アドルフ・ビューゼマン、ヘルマン・シュリヒティング、フランク・ホイットル、ハンス・フォン・オハインなどがいます。

歴史的貢献の部分的なタイムライン

表2.1
<1689 初期のターボマシン ポンプ、ブロワー、ファン
1689 デニス・パパン 遠心圧縮機の起源
1754 レオンハルト・オイラー オイラーのポンプ・タービン方程式
1791 ジョン・バーバー 最初のガスタービンの特許
1899 ACE ラトー 最初の実用的な遠心圧縮機
1927 オーレル・ボレスラフ・ストドラ 形式化された「スリップ係数」
1928 アドルフ・ブーゼマン 導出された「スリップ係数」
1937 フランク・ホイットルとハンス・フォン・オハインは独立して 遠心圧縮機を使用した最初のガスタービン
>1970 現代のターボマシン 3D-CFD、ロケットターボポンプ、心臓補助ポンプ、ターボチャージ燃料電池

ターボ機械の類似点

遠心圧縮機は多くの点で他のターボ機械と類似しており、次のように比較されます。

軸流圧縮機との類似点

軸遠心圧縮機ガスタービンの断面図

遠心圧縮機は、回転翼ベースの圧縮機であるという点で軸流圧縮機に似ています。両方とも、5段の軸流圧縮機と1段の遠心圧縮機を備えたエンジンの隣の写真に示されています。 [ 10 ]遠心インペラの最初の部分は、軸流圧縮機と非常によく似ています。遠心インペラのこの最初の部分はインデューサとも呼ばれます。遠心圧縮機は、インペラの入口から出口までの半径の大きな変化を利用して、軸流段よりもはるかに大きな圧力上昇を1段で生み出す点（たとえば、プラット・アンド・ホイットニー・カナダのヘリコプターエンジンシリーズのPW200では8 [ 19 ]）が軸流段とは異なります。 1940年代に開発されたドイツのハインケルHeS 011実験エンジンは、軸流式（無回転）と遠心式（90度）の中間の半径方向流れの方向転換角を持つ圧縮段を備えた最初の航空用ターボジェットエンジンでした。これは混流式／斜流式圧縮機として知られています。斜流式圧縮機は、プラット・アンド・ホイットニー・カナダ社の小型ターボファンエンジンPW600シリーズに採用されています。

遠心ファン

低速、低圧の遠心圧縮機または遠心ファン。上向きの排出コーンを使用して空気の速度を拡散する。

遠心圧縮機は、隣の図に示すタイプの遠心ファンとも類似しており、どちらも半径が大きくなるにつれて流れのエネルギーを増加させます。 [ 1 ]遠心ファンとは対照的に、圧縮機はより大きな圧力上昇を生み出すために高速で動作します。多くの場合、遠心ファンの設計に使用される工学的手法は遠心圧縮機の設計手法と同じであるため、非常によく似ていることがあります。

一般化と定義のために、遠心圧縮機は密度増加が5%を超えることが多いと言える。また、作動流体が空気または窒素の場合、相対流速はマッハ数0.3を超えることが多い[ 20 ]。一方、ファンやブロワーでは、密度増加は5%未満で、相対流速のピークはマッハ数0.3未満であることが多い。

リスかご型ファン

HVAC換気に使用される低速、低圧送風機

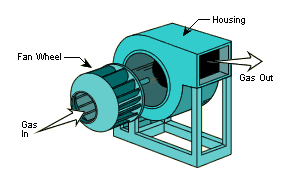
かご型ファンは主に換気に使用されます。このタイプのファン内の流れ場は内部循環を伴います。一方、遠心ファンは円周方向に均一な流れとなります。

遠心ポンプ

ある種の遠心ポンプの3Dソリッドモデル
遠心ポンプの断面図

遠心圧縮機は、隣の図に示すタイプの遠心ポンプ[ 1 ]にも似ています。これらの圧縮機とポンプの主な違いは、圧縮機の作動流体が気体（圧縮性）であるのに対し、ポンプの作動流体は液体（非圧縮性）である点です。繰り返しますが、遠心ポンプの設計に使用される工学的手法は、遠心圧縮機の設計手法と同じです。しかし、重要な違いが1つあります。それは、ポンプにおけるキャビテーションに対処する必要があることです。

遠心圧縮機と遠心ポンプは機械的なレイアウトは似ていますが、作動流体の圧縮性により設計目標が異なります。遠心圧縮機では、圧縮中のガス密度と温度の変化が、インペラの設計、ディフューザーの形状、そして全体的なステージ性能に大きな影響を与えます。一方、遠心ポンプは主に非圧縮性の液体を取り扱うため、運転中の密度は一定とみなすことができます。そのため、圧縮機では、サージ制御、チョーク限界、熱影響といった、ポンプ設計において一般的には重要ではない追加の考慮事項が必要になります。

遠心圧縮機では、エネルギーは主に回転するインペラを介してガスに伝達され、速度と圧力の両方が増加します。その後、高速のガスはディフューザーを通過し、そこで運動エネルギーの一部が静圧に変換されます。このプロセスは原理的には遠心ポンプと似ていますが、圧縮率の影響は圧縮機においてのみ顕著です。

気体は圧縮性であるため、遠心圧縮機では流路全体にわたって密度が変化し、圧力上昇と効率に影響を及ぼします。非圧縮性液体を用いたポンプ運転ではこのような密度変化が起こらないため、性能予測と制御が容易になります。

ラジアルタービン

図に示すように、遠心圧縮機はターボ機械のラジアルタービンと非常によく似ています。圧縮機がエネルギーを流れに伝達して圧力を上げるのに対し、タービンは逆に流れからエネルギーを抽出して圧力を下げます。つまり、動力は圧縮機に入力され、タービンから出力されます。

遠心圧縮機を用いたターボ機械

標準

ターボ機械の普及に伴い、メーカーがエンドユーザーに対し、自社製品が最低限の安全性と性能要件を満たしていることを保証するための規格が策定されてきました。これらの規格を制定するために設立された協会は、メーカー、エンドユーザー、そして関連する技術専門家の協力を得ています。これらの協会とその規格の一部を以下に示します。

アプリケーション

以下は、遠心圧縮機の用途の一部であり、それぞれの用途について、その一般的な特性を簡潔に説明しています。まず、最もよく知られている2つの遠心圧縮機の用途、すなわちガスタービンとターボチャージャーを挙げます。[ 10 ]

図4.1 –ジェットエンジンの断面図（遠心圧縮機とその他の部品）
図4.2 –遠心圧縮機とその他の部品を示すジェットエンジンの断面図

  • ガスタービンおよび補助動力装置において。[ 29 ]図4.1～4.2を参照
    現代のガスタービンは、その単純な形式では、ブレイトンサイクルで動作します。（図 5.1 を参照）軸流圧縮機と遠心圧縮機のいずれかまたは両方を使用して圧縮を行います。遠心圧縮機が最もよく使用されるガスタービンの種類には、小型航空機エンジン（ターボシャフト、ターボプロップ、ターボファン）、補助動力装置、マイクロタービンなどがあります。航空機用途のあらゆる遠心圧縮機に適用される業界標準は、運用に必要な安全性と耐久性を実現するために、関係する民間および軍事認証機関によって設定されています。ガスタービンで使用される遠心インペラは、一般的にチタン合金の鍛造品から作られています。その流路ブレードは、一般的に 5 軸フライス盤でフランクミルド加工またはポイントミルド加工されます。インペラがシュラウドに擦れることなく、ランニングクリアランスをできるだけ小さくする必要がある場合、インペラは最初に高温高速たわみ形状で引抜かれ、次に製造用に同等の冷間静的形状で引抜かれます。これが必要なのは、最も厳しい運転条件でのインペラのたわみが、インペラとシュラウド間の必要な高温運転クリアランスの 100 倍になる可能性があるためです。

  • パイプラインでは天然ガスを生産地から消費者まで輸送するためにコンプレッサーが使われます。 [ 31 ]
    このような用途の遠心圧縮機は、単段式または多段式で、大型ガスタービンによって駆動されます。業界標準（ANSI/API、ASME）では、必要な安全性を確保するためにケーシングが厚くなっています。インペラは、必ずしもそうとは限りませんが、多くの場合、カバー付きタイプで、ポンプのインペラによく似ています。このタイプの圧縮機は、APIタイプとも呼ばれます。これらの圧縮機の駆動に必要な電力は、ほとんどの場合、数千馬力です。ガスパイプライン用遠心圧縮機の性能を適切に設計、試験、分析するには、実在気体の特性を利用する必要があります。

  • 石油精製所、天然ガス処理工場、石油化学工場、化学工場など。[ 31 ]
    このような用途の遠心圧縮機は、多くの場合、1 軸多段式で、大型の蒸気タービンまたはガスタービンで駆動されます。 ケーシングは、組み立て時にローターが下半分に降ろされる場合は水平分割型、ローターをスライドさせて挿入する際に縦方向の分割線がない場合はバレル型と呼ばれます。 業界で定められたこれらの圧縮機の規格 (ANSI/API、ASME) では、必要な安全性レベルを達成するためにケーシングが厚くなっています。 インペラーはカバー付きスタイルであることが多く、ポンプのインペラーによく似ています。 このタイプの圧縮機は、しばしばAPI スタイルとも呼ばれます。 これらの圧縮機の駆動に必要な電力は通常、数千馬力になります。 性能を適切に設計、テスト、分析するには、実在気体の特性を利用する必要があります。

  • 産業および製造業では、あらゆる種類の空気圧工具に圧縮空気を供給する。[ 33 ]
    このような用途の遠心圧縮機は、多くの場合多段式で、電動モーターで駆動されます。各段の間には、空気の温度を制御するために中間冷却が必要になることがよくあります。道路修理作業員や自動車修理工場では、スクリュー圧縮機の方がニーズに合っていると感じています。これらの圧縮機に対して業界が定めた規格には、安全性を重視したASME規格や政府規制などがあります。これらの機械の性能を適切に設計、試験、解析するために、理想気体関係がよく用いられます。湿度を扱う際には、キャリアの式がよく用いられます。

  • 精製された最終製品ガスを製造する空気分離プラントにおいて。[ 33 ]
    このような用途の遠心圧縮機は、多くの場合多段式で、中間冷却によって空気の温度を制御します。これらの圧縮機に対して業界で定められた規格には、安全性を重視するASME規格や政府規制などがあります。作動ガスが空気または窒素の場合、これらの機械の性能を適切に設計、試験、解析するために、理想気体関係がよく用いられます。その他の気体の場合は、実在気体の特性が必要です。

  • 油田では高圧天然ガスを再注入することで石油回収率を向上させる。[ 31 ]
    このような用途の遠心圧縮機は、多くの場合、一軸多段式で、ガスタービンで駆動されます。吐出圧力が700barに近づくため、ケーシングはバレル型です。業界規格（API、ASME）では、これらの圧縮機に対して安全性を最大限に高めるために、ケーシングは大型で厚くなっています。インペラは、必ずしもそうとは限らないものの、多くの場合カバー型で、ポンプのインペラによく似ています。このタイプの圧縮機は、しばしばAPI型とも呼ばれます。これらの圧縮機の性能を適切に設計、試験、分析するには、実在気体の特性を利用する必要があります。

動作原理

流れが直管を通過して遠心圧縮機に入る場合、流れは軸方向に均一で、渦度、すなわち旋回運動を伴わない。流れが遠心インペラを通過すると、インペラは回転軸から離れるにつれて流れを速く回転させる。オイラーのポンプ・タービン方程式によれば、流体に入力されるエネルギーは、流れの局所的な回転速度とインペラの局所的な接線速度の積に比例する。

多くの場合、遠心羽根車を出た流れは音速に近い速度で流れます。その後、固定式圧縮機を通過して減速します。固定式圧縮機は、エネルギー変換が行われる流路面積が増加するように配管されています。機械の次の部分、例えば別の羽根車や燃焼器に流入するために流れを後方に曲げる必要がある場合は、固定式の転向羽根や個別の転向管（パイプディフューザー）を用いて流れを方向転換することで、流量損失を低減できます。ベルヌーイの定理によれば、速度の低下は圧力上昇を引き起こします。[ 1 ]

パフォーマンス

図5.1 –ガスタービンに適用されたブレイトンサイクルの図解
図5.2 – 遠心圧縮機の性能マップの例

ガスタービンのブレイトンサイクルを図解しながら、[ 15 ]図 5.1 には、圧力-比容積および温度-エントロピーのグラフ例が含まれています。これらのタイプのグラフは、1 つの動作点での遠心圧縮機の性能を理解する上で基本となります。2 つのグラフは、圧縮機の入口 (ステーション 1) と出口 (ステーション 2) の間で圧力が上昇することを示しています。同時に、比容積は減少し、密度が増加します。温度-エントロピーのグラフは、エントロピー (損失) が増加すると温度が上昇することを示しています。乾燥空気、理想気体の状態方程式、等エントロピー過程を仮定すると、この 1 つの点の圧力比と効率を定義するのに十分な情報が得られます。圧縮機マップは、その全動作範囲にわたる圧縮機の性能を理解するために必要です。

図5.2は、遠心圧縮機の性能マップ（試験結果または推定結果）であり、4つの速度線（合計23のデータポイント）ごとに流量と圧力比を示しています。また、定効率等高線も含まれています。この形式で示される遠心圧縮機の性能は、マップに示されたハードウェアをエンドユーザーの要件に適合させるのに十分な情報を提供します。

性能の推定は非常に費用対効果が高く（したがって設計に有用である）、それに比べ試験は費用はかかるものの、依然として最も正確な方法である。[ 12 ]さらに、遠心圧縮機の性能試験は非常に複雑である。ASME（すなわちPTC–10、流体計量器ハンドブック、PTC-19.x）[34] ASHRAE（ASHRAEハンドブック）およびAPI（ANSI/API 617–2002、672–2007）[31] [33] などの専門団体は、詳細な実験方法と試験結果の分析に関する標準規格を制定している。このような複雑さにもかかわらず、試験性能マップの例を調べることで、性能に関するいくつかの基本概念を示すことができる。

パフォーマンスマップ

圧力比と流量は、図5.2の性能マップを単純な圧縮機アプリケーションに適合させるために必要な主要なパラメータ[ 15 ] [ 31 ] [ 33 ] [ 34 ]である。この場合、入口温度は海面基準であると仮定できる。しかし、入口温度の変動は圧縮機性能に大きな変動をもたらすため、この仮定は実際には受け入れられない。図5.2は以下のことを示している。

  • 補正質量流量: 0.04～0.34 kg/s
  • 全圧比、入口対出口（PR t-t = P t,discharge /P t,inlet）：1.0～2.6

図5.2では、標準的な方法に従い、横軸に流量パラメータが示されています。流量測定には様々な単位が用いられますが、いずれも単位時間当たりの質量流量または単位時間当たりの体積流量の2つのカテゴリのいずれかに該当します。

単位時間あたりの質量流量

kg/sなどの質量流量単位は、混乱の余地がほとんどないため、実用上最も使いやすい単位です。残る疑問としては、入口か出口か（圧縮機からの漏れや結露が関係する可能性がある）が挙げられます。大気の場合、質量流量は湿潤状態か乾燥状態か（湿度を含む場合と含まない場合）のどちらかです。質量流量の仕様は、多くの場合、等価マッハ数に基づいて示されます。[ 35 ]このような場合、等価温度、等価圧力、およびガスが標準状態において明示的または暗黙的に指定されるのが一般的です。 メートルθ/δ{\displaystyle m{\sqrt {\theta}}/{\delta}}

単位時間あたりの体積流量

対照的に、体積流量の仕様はすべて、密度という追加の仕様を必要とします。ベルヌーイの定理は、この問題を理解する上で非常に役立ちます。混乱は、圧力、温度、および気体定数の不正確さや誤用によって生じます。

また、図5.2では標準的な方法に従い、縦軸に圧力パラメータが示されています。圧力測定単位には様々な種類があり、いずれも以下の2つのカテゴリのいずれかに該当します。

  • 圧力の変化、つまり入口から出口への圧力の増加（圧力計で測定）
  • 排出圧力

圧力上昇は、単位のない比率として指定することもできます。

  • 圧力比（出口/入口）

パフォーマンス マップに共通するその他の機能としては、定速ライン、定効率アイランド、設計ポイントまたは保証ポイントなどがあります。

定速線

遠心圧縮機のマップを作成する最も一般的な方法は、シャフト速度一定とスロットル設定一定という2つです。速度が一定に保たれる場合、スロットル位置を変更することで定速ラインに沿ってテストポイントが設定されます。一方、スロットルバルブが一定に保たれる場合、速度を変更することでテストポイントが設定され、異なるスロットル位置で繰り返し実行されます（一般的なガスタービンの手法）。図5.2に示すマップは、最も一般的な方法である定速ラインを示しています。この例では、50%、71%、87%、100% RPMの速度でデータポイントが直線で結ばれています。最初の3つの速度ラインにはそれぞれ6つのポイントがあり、最も高い速度ラインには5つのポイントがあります。

一定効率の島々

次に説明する特徴は、等効率の島を表す楕円形の曲線です。この図には、56%効率（小数点0.56）から76%効率（小数点0.76）までの11本の等高線があります。一般的な標準的な解釈では、これらの効率はポリトロープではなく等エントロピーとして解釈されます。効率の島を含めることで、この2次元マップは実質的に3次元トポロジーを生成します。入口密度を指定することで、空力出力をさらに計算できるようになります。等効率線で置き換えることも同様に可能です。

設計または保証ポイント

ガスタービンの運転と性能に関しては、ガスタービンの遠心圧縮機に一連の保証点が設定されている場合があります。これらの要件は、ガスタービン全体の性能に比べると二次的な重要性しかありません。したがって、理想的なケースでは、遠心圧縮機のピーク効率曲線がガスタービンの要求運転ラインと一致するときに、燃料消費率が最も低くなるとだけ述べておく必要があります。

ガスタービンとは対照的に、他のほとんどの用途（産業用途を含む）では、それほど厳しくない性能要件を満たす必要があります。歴史的に、産業用途に適用される遠心圧縮機は、特定の流量と圧力で性能を達成する必要がありました。現代の産業用圧縮機は、多くの場合、幅広い流量と圧力にわたって特定の性能目標を達成することが求められており、ガスタービン用途に見られるような高度化に向けて大きく前進しています。

図5.2に示すコンプレッサを単純なアプリケーションで使用する場合、効率76%以内のどのポイント（圧力と流量）でも非常に良好な性能が得られます。エンドユーザーは、0.21 kg/sで圧力比2.0という性能要件を満たせば非常に満足できるでしょう。

うねり

サージは低流量現象であり、インペラがシステム抵抗または背圧を克服するのに十分なエネルギーを加えることができない。[ 36 ]低流量動作では、インペラ上の圧力比が高く、背圧も高い。危機的な状況では、流れはローターブレードの先端を越えてインペラの目（入口）に向かって逆戻りする。[ 37 ]この失速する流れの逆転は、質量流量またはエネルギーの割合が低すぎると気付かない可能性がある。十分に大きい場合、急速な流れの逆転が発生する（すなわち、サージ）。インペラ入口から出る逆流は強い回転成分を示し、ブレードの前縁での半径の小さい流れ角度（インペラハブに近い方）に影響を与える。流れ角度の悪化は、イ​​ンペラの効率を低下させる。完全な流れの逆転が発生する可能性がある。 （そのため、サージは軸対称失速と呼ばれることもあります。）逆流が十分に低いレベルまで減少すると、インペラは回復して短時間安定状態に戻りますが、その時点でステージが再びサージする可能性があります。これらの周期的なイベントは大きな振動を引き起こし、温度を上昇させ、軸方向の推力を急激に変化させます。これらの発生は、ローターシール、ローターベアリング、コンプレッサードライバー、およびサイクル動作に損傷を与える可能性があります。ほとんどのターボ機械は、偶発的なサージに容易に耐えられるように設計されています。しかし、機械が長期間にわたって繰り返しサージを強いられる場合、または設計が不十分な場合は、繰り返されるサージが壊滅的な故障につながる可能性があります。特に興味深いのは、ターボ機械は非常に耐久性が高いかもしれませんが、その物理的システムの堅牢性ははるかに低い場合があるということです。

サージライン

図6.2.1: 失速形成

図5.2に示すサージラインは、4つの速度線それぞれの最低流量点を通る曲線です。試験マップとして、これらの点は試験施設／試験装置内で安定した測定値を記録できる最低流量点となります。多くの産業用途では、システムの背圧のために失速ラインを上昇させる必要がある場合があります。例えば、100% RPMでは、圧力比曲線の正の傾きにより、失速流量が約0.170 kg/sから0.215 kg/sに増加する可能性があります。

前述の通り、これは図5.2の高速ラインがその流量範囲において失速特性、つまり正の勾配を示すためです。別のシステムに設置した場合、そのシステムとの相互作用により、これらの低流量を達成できない可能性があります。システム抵抗または逆圧は、コンプレッサーサージの重要な要因であることが数学的に証明されています。

最大流量ラインとチョーク

チョークは2つの条件のいずれかで発生します。一般的に高速機器では、流量が増加すると、圧縮機段内のどこかで流速が音速に近づくことがあります。この場所は、インペラの入口「スロート」またはベーン付きディフューザーの入口「スロート」で発生する可能性があります。一方、低速機器では、流量が増加すると損失が増加し、最終的に圧力比が1:1に低下します。この場合、チョークが発生する可能性は低くなります。

ガスタービン遠心圧縮機の速度線は、典型的にはチョーク現象を示します。これは、流量にほとんど変化がない、あるいは全く変化がない状態で、速度線上の圧力比が急激に（垂直方向に）低下する状態です。ほとんどの場合、この原因は、インペラまたはディフューザー内のどこかでマッハ1に近い速度に達し、損失が急激に増加することです。高圧力比ターボチャージャー遠心圧縮機でも同じ現象が見られます。実際のチョーク現象は、遠心圧力段内の制限された領域内の局所マッハ数で測定される圧縮率の関数です。

図5.2に示す最大流量線は、各速度線における最高流量点を通る曲線です。よく見ると、これらの点はいずれも効率56%付近で取得されていることがわかります。高流量域での圧縮機性能マップの終点として、低い効率（60%未満）を選択するのが最も一般的な方法です。最大流量線を確立するために用いられるもう一つの要素は、圧力比が1に近いか等しいことです。50%速度線はその一例と言えるでしょう。

図5.2の速度線の形状は、すべての遠心圧縮機の速度線において、最大流量と関連して「チョーク」という用語を使用することが不適切である理由を示す良い例です。要約すると、ほとんどの産業用および商業用の遠心圧縮機は、最高効率またはその近傍で動作するように選択または設計されており、低効率での運転は避けられています。このため、60%未満の効率で遠心圧縮機の性能を示す必要性はほとんどありません。

多くの産業用および商用の多段式コンプレッサーの性能マップは、ステージスタッキングと呼ばれるものに関連する別の理由により、この同じ垂直特性を示します。

その他の動作制限

最小動作速度
許容可能な動作の最小速度。この値を下回ると、コンプレッサーは停止するかアイドル状態になるように制御される場合があります。
最大許容速度
コンプレッサーの最大運転速度。この値を超えると、応力が規定の限界を超え、ローターの振動が急激に増加する可能性があります。この速度を超えると、機器は非常に危険な状態になり、低速運転に制御される可能性があります。

次元解析

遠心圧縮機の利点を比較検討するには、ターボ機械に典型的な8つのパラメータ、すなわち圧力上昇（p）、流量（Q）、角速度（N）、出力（P）、密度（ρ）、直径（D）、粘度（μ）、弾性率（e）を比較することが重要です。これらのパラメータのいずれか1つだけを独立して変化させることはほぼ不可能であるため、実験的にその影響を決定しようとすると、実際的な問題が生じます。

バッキンガムのπ定理は、これらのパラメータの5つの無次元形式を生成することで、この問題の解決に役立ちます。[ 1 ] [ 16 ]これらのパラメータは、ターボ機械における「相似則」と「親和性則」の基礎となります。これらは、性能特性評価において有用な、（無次元である）追加の関係式の構築を可能にします。

以下の例では、圧力の代わりにヘッドが使用され、弾性の代わりに音速が使用されます。

バッキンガムのΠ定理

ターボ機械のこの手順で使用される 3 つの独立した寸法は次のとおりです。

  • M{\displaystyle M}質量（力は代替手段）
  • L{\displaystyle L}長さ
  • T{\displaystyle T}時間

定理によれば、8 つの主なパラメータはそれぞれ、次のように独立した次元に等しくなります。

流れ 質問＝{\displaystyle Q=}L3T{\displaystyle {\frac {L^{3}}{T}}}例 = m 3 /s
頭 H＝{\displaystyle H=}MLT2{\displaystyle {\frac {ML}{T^{2}}}}例 = kg·m/s 2
スピード あなた＝{\displaystyle U=}LT{\displaystyle {\frac {L}{T}}}例 = m/s
力 P＝{\displaystyle P=}ML2T3{\displaystyle {\frac {ML^{2}}{T^{3}}}}例 = kg·m 2 /s 3
密度 ρ＝{\displaystyle \rho =}ML3{\displaystyle {\frac {M}{L^{3}}}}例 = kg/m 3
粘度 μ＝{\displaystyle \mu =}MLT{\displaystyle {\frac {M}{LT}}}例 = kg/m·s
直径 D＝{\displaystyle D=}L{\displaystyle L}例 = m
音速 1つの＝{\displaystyle a=}LT{\displaystyle {\frac {L}{T}}}例 = m/s

古典的なターボ機械の相似

正式な手順に従う作業を完了すると、ターボ機械の5つの無次元パラメータからなる典型的なセットが生成されます。[ 1 ] 2つの異なるケースを比較した際に、5つのπパラメータのそれぞれが等しい場合、完全な相似性が達成されます。これは、比較対象となる2つのターボ機械が、幾何学的にも性能的にも類似していることを意味します。

古典的な無次元相似パラメータの表
1 流量係数 Π1＝{\displaystyle \Pi _{1}=}質問北D3{\displaystyle {\frac {Q}{ND^{3}}}}
2 ヘッド係数 Π2＝{\displaystyle \Pi _{2}=}グラムH北2D2{\displaystyle {\frac {gH}{N^{2}D^{2}}}}
3 速度係数 Π4＝{\displaystyle \Pi _{4}=}北D1つの{\displaystyle {\frac {ND}{a}}}
4 べき乗係数 Π3＝{\displaystyle \Pi _{3}=}Pρ北3D5{\displaystyle {\frac {P}{\rho N^{3}D^{5}}}}
5 レイノルズ係数 Π5＝{\displaystyle \Pi _{5}=}ρ北D2μ{\displaystyle {\frac {\rho ND^{2}}{\mu }}}

ターボ機械の解析者は、上記の表に示す5つのパラメータ、特に効率や損失係数といった無次元パラメータを比較することで、性能に関する洞察を得ます。一般的な用途では、流量係数と揚程係数が最も重要と考えられています。一般的に、遠心圧縮機では速度係数が2番目に重要であり、レイノルズ係数が3番目に重要です。一方、ポンプの場合、レイノルズ係数は2番目に重要であり、速度係数が3番目に重要となります。図1.1のy軸を定義するために速度係数を選択し、同時にレイノルズ係数をz軸として選択できることは興味深いことです。

その他の無次元の組み合わせ

下の表は次元解析のもう一つの価値を示しています。指数と乗算によって、任意の数の新しい無次元パラメータを計算することができます。例えば、下に示す最初のパラメータのバリエーションは、航空機エンジンシステムの解析で広く用いられています。3番目のパラメータは、1番目と2番目のパラメータを簡略化した次元バリエーションです。この3番目の定義は、厳しい制限付きで適用可能です。4番目のパラメータである比速度は、直径を除外できるという点で非常によく知られており、有用です。5番目のパラメータである比直径は、あまり議論されていない無次元パラメータですが、Baljeによって有用であることが発見されました。[ 38 ]

1 補正質量流量係数 Π1Π4＝{\displaystyle \Pi _{1}\Pi _{4}=}メートルpD2（Rtけ）0.5{\displaystyle {\frac {m}{pD^{2}}}\left({\frac {Rt}{k}}\right)^{0.5}}
2 代替#1相当のマッハ形式 メートル1ρ11つの1D12コス⁡（α1）＝{\displaystyle {\frac {m_{1}}{\rho _{1}a_{1}{D_{1}}^{2}\cos(\alpha _{1})}}=}}メートル2ρ21つの2D22コス⁡（α2）{\displaystyle {\frac {m_{2}}{\rho _{2}a_{2}{D_{2}}^{2}\cos(\alpha _{2})}}}
3 代替案#2 簡略化された次元形式 メートル1t10.5p1＝{\displaystyle {\frac {m_{1}{t_{1}}^{0.5}}{p_{1}}}=}メートル2t20.5p2{\displaystyle {\frac {m_{2}{t_{2}}^{0.5}}{p_{2}}}}
4 比速度係数 Π10.5Π20.75＝{\displaystyle {\frac {{\Pi _{1}}^{0.5}}{{\Pi _{2}}^{0.75}}}=}北質問0.5（グラムH）0.75{\displaystyle {\frac {NQ^{0.5}}{(gH)^{0.75}}}}
5 比直径係数 Π20.25Π10.5＝{\displaystyle {\frac {{\Pi _{2}}^{0.25}}{{\Pi _{1}}^{0.5}}}=}D（グラムH）0.25質問0.5{\displaystyle {\frac {D(gH)^{0.25}}{Q^{0.5}}}}

図 1.2 の y 軸を定義するために速度の代わりに特定の速度係数が使用される一方で、z 軸を定義するために直径の代わりに特定の直径係数が使用される可能性があることは興味深いことです。

親和性の法則

以下の親和力則は、上記に示した5つのΠパラメータから導かれます。これらは、ターボ機械をある用途から次の用途へとスケーリングするためのシンプルな基礎を提供します。

流量係数から 質問1質問2＝{\displaystyle {\frac {Q_{1}}{Q_{2}}}=}北1北2＝{\displaystyle {\frac {N_{1}}{N_{2}}}=}（D1D2）3{\displaystyle \left({\frac {D_{1}}{D_{2}}}\right)^{3}}
頭部係数から H1H2＝{\displaystyle {\frac {H_{1}}{H_{2}}}=}（北1北2）2＝{\displaystyle \left({\frac {N_{1}}{N_{2}}}\right)^{2}=}（D1D2）2{\displaystyle \left({\frac {D_{1}}{D_{2}}}\right)^{2}}
べき乗係数から P1P2＝{\displaystyle {\frac {P_{1}}{P_{2}}}=}（北1北2）3＝{\displaystyle \left({\frac {N_{1}}{N_{2}}}\right)^{3}=}（D1D2）5{\displaystyle \left({\frac {D_{1}}{D_{2}}}\right)^{5}}

空気熱力学の基礎

以下の方程式は、仮定を単純化しても解くのが非常に難しい完全な3次元数学の問題を概説しています。[ 10 ] [ 39 ]最近まで、計算能力の限界により、これらの方程式は擬似損失を伴う非粘性2次元問題に簡略化せざるを得ませんでした。コンピュータの登場以前は、これらの方程式はほぼ常に1次元問題に簡略化されていました。この1次元問題を解くことは今日でも価値があり、しばしば平均線解析と呼ばれます。このように単純化されたとしても、その概要を説明するには依然として大判の教科書が必要であり、実際に解くには大規模なコンピュータプログラムが必要です。

質量保存則

連続性とも呼ばれるこの基本方程式を一般的な形で書くと次のようになります。

∂ρ∂t+∇⋅（ρv）＝0{\displaystyle {\frac {\partial \rho }{\partial t}}+\nabla \cdot (\rho \mathbf {v} )=0}

運動量保存則

ナビエ・ストークス方程式とも呼ばれるこの基本方程式は、ニュートン力学の第二法則を流体の運動に適用することで導出されます。ニュートン流体の圧縮性形式で記述すると、この方程式は次のように表されます。

ρ（∂v∂t+v⋅∇v）＝−∇p+μ∇2v+（13μ+μv）∇（∇⋅v）+f{\displaystyle \rho \left({\frac {\partial \mathbf {v} }{\partial t}}+\mathbf {v} \cdot \nabla \mathbf {v} \right)=-\nabla p+\mu \nabla ^{2}\mathbf {v} +\left({\frac {1}{3}}\mu +\mu ^{v}\right)\nabla \left(\nabla \cdot \mathbf {v} \right)+\mathbf {f} }

エネルギー保存則

熱力学第一法則はエネルギー保存則を規定するものです。特定の条件下では、遠心圧縮機の運転は可逆過程とみなされます。可逆過程において、系に加えられる熱の総量は と表されます。ここでは温度、はエントロピーです。したがって、可逆過程の場合： δQ=TdS{\displaystyle \delta Q=TdS}T{\displaystyle T}S{\displaystyle S}

dU=TdS−pdV.{\displaystyle dU=TdS-pdV.\,}

U、S、Vは熱力学的な状態関数であるため、上記の関係は不可逆な変化にも当てはまります。上記の式は、基本的な熱力学関係として知られています。

状態方程式

古典的な理想気体の法則は次のように記述されます。

 pV=nRT.{\displaystyle {\ pV=nRT}.}

理想気体の法則は次のようにも表される。

 p=ρ(γ−1)U,{\displaystyle {\ p=\rho (\gamma -1)U},}

ここで、 は密度、は断熱指数（比熱比）、は単位質量あたりの内部エネルギー（「特定の内部エネルギー」）、は定積比熱、 は定圧比熱です。 ρ{\displaystyle \rho }γ=Cp/Cv{\displaystyle \gamma =C_{p}/C_{v}}U=CvT{\displaystyle U=C_{v}T}Cv{\displaystyle C_{v}}Cp{\displaystyle C_{p}}

状態方程式に関して、空気と窒素の特性（標準大気圧に近い状態）はこの単純な関係式によって容易かつ正確に推定できるものの、多くの遠心圧縮機の用途ではこの理想的な関係式が適切ではないことを覚えておくことが重要です。例えば、大型空調システム（水冷却装置）に使用される遠心圧縮機は、理想気体としてモデル化できない冷媒を作動ガスとして使用します。別の例としては、石油産業向けに設計・製造された遠心圧縮機があります。メタンやエチレンなどの炭化水素ガスのほとんどは、理想気体の法則ではなく、実在気体の状態方程式によって最もよくモデル化されます。

長所と短所

長所
  • 遠心圧縮機は、製造が簡単で比較的低コストという利点があります。これは、同じ圧力上昇を達成するために必要な段数が少ないためです。
  • 遠心圧縮機は、同サイズの往復圧縮機やその他の容積式ポンプに比べて、摩擦部品が少なく、比較的エネルギー効率が高く、振動のない一定の空気流を生み出すため、産業界全体で使用されています。
  • 遠心圧縮機は、主にターボチャージャー、補助動力装置などの小型ガスタービンエンジン、そしてヘリコプターなどの小型航空機の主エンジンとして使用されています。その主な理由は、現在の技術では、等価空気流量の軸流圧縮機は、主にローターと可変ステーターのチップクリアランス損失の組み合わせにより、効率が低下するためです。
短所
  • 主な欠点は、多段式でないと往復動型圧縮機のような高い圧縮比を実現できないことです。1段遠心型圧縮機で10:1を超える圧力比を実現できるものはほとんどありません。これは、圧縮機の安全性、耐久性、寿命を著しく制限する応力を考慮する必要があるためです。
  • 遠心圧縮機は、結果として生じる重量と応力、およびラジアルディフューザーの大きな直径によって生じる前面面積のために、軸流圧縮機と比較して、大型の航空機を推進する大型ガスタービンやターボジェットエンジンで使用するには実用的ではありません。

構造力学、製造、設計の妥協

理想的には、遠心圧縮機のインペラは、薄くて強度の高い翼型ブレードを軽量のローターに取り付けた構造です。この材料は機械加工や鋳造が容易で安価です。さらに、運転音も発生せず、あらゆる環境で長寿命を実現します。

空力熱力学設計プロセスの最初から、空力的な考慮と最適化[29,30]は設計の成功に不可欠です。設計段階では、遠心インペラの材質と製造方法を考慮する必要があります。掃除機用送風機の場合はプラスチック、ターボチャージャーの場合はアルミニウム合金、空気圧縮機の場合は鋼合金、ガスタービンの場合はチタン合金などです。遠心圧縮機インペラの構造的完全性は、遠心圧縮機インペラの形状、動作環境、材質、製造方法の組み合わせによって決まります。[ 40 ] [ 41 ]

参照

参考文献

  1. ^ a b c d e f g h i j k l m n Shepherd, Dennis G. (1956). Principles of turbomachinery (6th ed.). New York: Macmillan . LCCN  56002849 . OCLC  5899719 .
  2. ^ a b Japikse, David (1996).遠心圧縮機の設計と性能. Concepts ETI. ISBN 978-0-933283-03-9。
  3. ^ Whitfield, A.; Baines, NC (1990).ラジアルターボ機械の設計. Longman Scientific and Technical. ISBN 978-0-470-21667-5。
  4. ^ a b c Aungier, Ronald H. (2000).遠心圧縮機：空力設計と解析のための戦略. ASME Press. ISBN 978-0-7918-0093-5。
  5. ^ a bジャピクセ、デイビッド;ノースカロライナ州ベインズ (1998)。ディフューザー設計技術。概念 ETI 。ISBN 978-0-933283-01-5。
  6. ^ Heinrich, Martin ; Schwarze, Rüdiger (2016年1月). 「遠心圧縮機の渦形形状の遺伝的アルゴリズムによる最適化」 . International Journal of Rotating Machinery . 2016 : 1–13 . doi : 10.1155/2016/4849025 .
  7. ^ Aurel Stodola (1945).蒸気タービンとガスタービン. ニューヨーク: P. Smith. OL 18625767M . 
  8. ^プフライデラー、C. (1952)。ターボマシン。ニューヨーク: Springer-Verlag。
  9. ^ WR Hawthorne (1964). 『タービンとコンプレッサーの空気力学』プリンストン大学出版局, ニュージャージー州, LCCN 58-5029 . 
  10. ^ a b c d Lakshminarayana, B. (1996).流体力学とターボ機械の熱伝達. ニューヨーク: John Wiley & Sons Inc. ISBN 978-0-471-85546-0。
  11. ^ Japikse, David; Baines, Nicholas C. (1997). 『ターボ機械入門』オックスフォード: オックスフォード大学出版局. ISBN 978-0-933283-10-7。
  12. ^ a b Japikse, David (1986年12月).ターボ機械における高度な実験技術. Concepts ETI. ISBN 978-0-933283-01-5。
  13. ^ Peng, WW (2007). 『ターボ機械の基礎』ニューヨーク: John Wiley & Sons Inc. ISBN 978-0-470-12422-2。
  14. ^ a b c d e f g h Wislicenus, George Friedrich (1965). Fluid Mechanics of Turbomachinery in two volumes . New York: Dover. ISBN 978-0-486-61345-1。
  15. ^ a b c d Wood, Bernard D. (1969). 『熱力学の応用』 マサチューセッツ州レディング: Addison-Wesley Publishing Company. LCCN 75-79598 . 
  16. ^ a b cストリーター、ビクター・L.（1971年）『流体力学 第5版』ニューヨーク：マグロウヒル・ブック・カンパニー。ISBN 978-0-07-062191-6。
  17. ^エンゲダ、エイブラハム (1999). 「水晶宮からポンプ室へ」 .機械工学. ASME. 2009年1月15日時点のオリジナルよりアーカイブ。
  18. ^エリオット社. 「過去、現在、未来、1910-2010」(PDF) . エリオット. 2011年5月1日閲覧。
  19. ^ =ジェットおよびタービン航空エンジンの開発第4版、ビル・ガンストン2006年、 ISBN 0 7509 4477 3、217ページ
  20. ^ API (2002年7月). Std 673-2002 石油、化学、ガス産業向け遠心ファン. ニューヨーク: API.
  21. ^アメリカ機械学会. 「ASME BPVC」 . www.asme.org . ASME . 2021年12月13日閲覧。
  22. ^アメリカ機械学会. 「ASME PTC」 . www.asme.org . ASME . 2021年12月13日閲覧。
  23. ^アメリカ石油協会. 「API STD 617 第8版 (E1)」 . www.api.org . アメリカ石油協会. 2021年12月13日閲覧。
  24. ^アメリカ石油協会. 「API STD 672 第5版 (2019)」 . www.api.org . アメリカ石油協会. 2021年12月13日閲覧。
  25. ^ 「2021 ASHRAEハンドブック—基礎」の説明。www.ashrae.org。2022年2月20日閲覧。
  26. ^ a b「SAE規格」 SAE /standards/power and propulsion/enginesSAE International . 2011年4月23日閲覧。
  27. ^圧縮空気・ガス協会. 「CAGI」 . www.cagi.org . 圧縮空気・ガス協会. 2021年12月13日閲覧。
  28. ^ ISO. 「ISO - 検索」 .国際標準化機構. 2021年12月13日閲覧。
  29. ^サラヴァナムトゥー, HIH; ロジャース, GFC; コーエン, H. (2001).ガスタービン理論. プレンティス・ホール. ISBN 978-0-13-015847-5。
  30. ^ベインズ、ニコラス・C. (2005). 『ターボチャージングの基礎』 . Concepts ETI. ISBN 978-0-933283-14-5。
  31. ^ a b c d e API (2002年7月). Std 617-2002 石油、化学、ガス産業向け軸流・遠心圧縮機および膨張圧縮機. ニューヨーク: API.
  32. ^ ASHRAE（アメリカ暖房冷凍空調学会）「規格とガイドライン」 ASHRAE . 2011年4月23日閲覧。{{cite web}}: CS1 maint: multiple names: authors list (link)
  33. ^ a b c d API (2007年10月). Std 672-2007 石油、化学、ガス産業向けパッケージ型一体型ギア付き遠心空気圧縮機. ニューヨーク: API.
  34. ^ a b ASME PTC 10-1997 圧縮機および排気装置の試験規格ニューヨーク: ASME. 1997. ISBN 978-0-7918-2450-4。
  35. ^遠心圧縮機基本ガイド、ボイス 2003、 ISBN 0 87814 801 9図2-11 典型的な遠心圧縮機の性能マップ
  36. ^パンプリーン、ロナルド・C. (1993).コンプレッサーのサージと失速. Concepts ETI. ISBN 978-0-933283-05-3。
  37. ^ Semlitsch, Bernhard; Mihăescu, Mihai (2016年5月). 「遠心圧縮機におけるサージにつながる流動現象」 . Energy . 103 : 572–587 . Bibcode : 2016Ene...103..572S . doi : 10.1016/j.energy.2016.03.032 .
  38. ^ Balje, OE (1961). 『ターボマシン：設計、選定、理論ガイド』ニューヨーク：John Wiley & Sons. ISBN 978-0-471-06036-9。{{cite book}}: ISBN / Date incompatibility (help)
  39. ^ Cumpsty, NA (2004).コンプレッサーの空気力学. Krieger Publishing. ISBN 978-1-57524-247-7。
  40. ^ Xu, C. および RS Amano、「遠心圧縮機インペラの開発」、International Journal for Computational Methods in Engineering Science and Mechanics、第 10 巻第 4 号 2009 年、290 ～ 301 ページ。
  41. ^ Xu, C., 遠心圧縮機開発における設計経験と考慮事項、J. of Aerospace Eng. 2007
ウィキメディア コモンズには、遠心圧縮機に関連するメディアがあります。
「 https://en.wikipedia.org/w/index.php?title=遠心圧縮機&oldid =1334329941」より取得