パチパチという音

木を燃やすとランダムにパチパチという音が出る

パチパチというノイズは、システムが外力を受け、多くの異なるスケールで非常によく似ているように見えるイベントを介して応答するときに発生します。古典的なシステムでは通常、オンとオフの 2 つの状態があります。ただし、その中間の状態が存在することもあります。このノイズは主に 3 つのカテゴリに分類できます。1 つ目はポッピングで、非常に同じ大きさのイベントが継続的かつランダムに発生します (ポップコーンなど)。2 つ目はスナップで、臨界しきい値を超えるまでシステムにほとんど変化がなく、その時点でシステム全体がある状態から別の状態に切り替わります (鉛筆を折る音など)。3 つ目はパチパチで、ポッピングとスナップが組み合わさったもので、いくつかの小さなイベントといくつかの大きなイベントがあり、その発生を予測する関係法則 (普遍性)があります。^{[ 1 ]}パチパチ音は多くの自然現象で観察できます。例えば、紙をくしゃくしゃにしたとき、^{[ 2 ]}キャンディーの包み紙（またはその他の弾性シート）、^{[ 3 ] [ 4 ]}火事、地震の発生、強磁性体の磁化などです。

クラッキングノイズは、スナップノイズやポッピングノイズとは対照的です。スナップノイズは1つの大きな降伏現象ですが、ポッピングノイズは同程度のサイズの小さな降伏現象が一定レベルで発生するものです。クラッキングノイズはこれらの中間に位置します。クラッキングノイズは、システムのコンポーネント間の接続強度が臨界レベルに達し、数桁にわたるサイズの降伏現象が多数発生する場合に発生します。^{[ 5 ]}

これらのシステムの中には、消磁（磁石をキュリー温度まで加熱することによる）のように可逆的なものもあれば、^{[ 6 ]}雪崩（雪は山を滑り落ちることしかできない）のように不可逆的なものもあるが、多くのシステムには、重力や他の外力のように、最終的にある状態から別の状態に移行する正のバイアスがある。

理論

バルクハウゼンノイズ

強磁性材料における磁化（J）または磁束密度（B）曲線と磁場強度（H）の関係。挿入図はバルクハウゼンノイズの原因となるジャンプを示している。

大きな磁区内の小さな摂動に関する研究は、1910年代後半にハインリヒ・バルクハウゼンが強磁性体内の磁区、すなわち双極子が外部磁場の影響下でどのように変化するかを研究したことに始まります。磁化が解除されると、磁石の双極子はランダムな方向を向くため、すべての双極子から生じる正味の磁力はゼロになります。鉄棒を電線で巻き、その電線に電流を流すと、コイルに垂直な磁場が生成されます（コイルにおけるフレミングの右手の法則）。これにより、磁石内の双極子は外部磁場と一直線になります。

当時、これらの磁区は一つずつ連続的に反転すると考えられていたのとは対照的に、バルクハウゼンは磁区のクラスターが小さな離散的なステップで反転することを発見した。^{[ 7 ]}スピーカーまたは検出器に接続されたバーの周りに二次コイルを巻き付けると、磁区のクラスターの配列が変化すると磁束の変化が発生し、二次コイルの電流が乱されて信号が出力される。これを大音量で再生すると、これはバルクハウゼンノイズと呼ばれ、磁石の磁化は磁束密度の関数として離散的なステップで増加する。^{[ 8 ]}

米国の地震記録（1930年～1987年）で発生したパチパチという音。データセットはNOAA、米国地震強度データベース（1638～1985年）より。

グーテンベルク・リヒターの法則

パチパチ音に関するさらなる研究は、1940年代後半に地震を分析的に調べたチャールズ・フランシス・リヒターとベノ・グーテンベルクによって行われました。よく知られているリヒタースケールが発明される前は、メルカリの震度スケールが使用されていました。これは、地震が建物にどれだけの損害を与えたかを主観的に測定するもので、IIは小さな振動と物体の移動、XIIはすべての建物の広範囲にわたる破壊を表します。リヒタースケールは、地震の震源から拡散した振動のエネルギーと振幅を測定する対数スケールで、たとえばマグニチュード7.0の地震は、6.0の地震の10倍の強さです。グーテンベルクとともに、彼らは地震のマグニチュードと発生確率の確率分布関係であるグーテンベルク・リヒターの法則を発見しました。これは、小さな地震ははるかに頻繁に発生し、大きな地震は非常にまれにしか発生しないことを示しています。^{[ 9 ]}

${\displaystyle N=10^{a-bM}}$

グーテンベルク・リヒターの法則^{[ 10 ]}は、発生する地震の数NとそのマグニチュードMの間に比例定数bと切片 aを伴う逆べき乗関係があることを示している。

シミュレーション

2次元セルオートマトンシミュレーションの経時的な変化。最初はシステムがポップ音を立て、次にいくつかの小さなクラスターといくつかの大きなクラスターが白くなり、白のままになるというパチパチという音が鳴り、最終的にシステムは全体的に正の状態（+1）に戻ります。

このような環境を真にシミュレートするには、連続した無限の3次元システムが必要ですが、計算上の制約により、2次元セルオートマトンを用いて近似値を得ることができます。1000×1000の行列に100万個のセルを置けば、ほとんどのシナリオをテストするのに十分です。各セルには2つの情報が保存されます。1つはセルに加えられた力（連続値）であり、もう1つはセルの状態（+1（オン）または-1（オフ）の整数値）です。

パラメータ化

ネットフォースは、あらゆるクラックルノイズシステムの物理的特性に対応する3つの要素から構成されます。1つ目は、時間(t)とともに増加する外部力場(K)です。2つ目は、隣接するセルの状態(S)の合計に依存する力です。3つ目は、(X)によってスケールされるランダムな要素(r)です^{[ 11 ]。}

${\displaystyle F_{i}=Kt+\Sigma JS_{i}+Xr_{i}}$

外力 K には時間 ( t ) が掛けられます。ここでKは正のスカラー定数ですが、変化したり負になったりすることもあります。S はセルの状態 (+1 または -1) を表し、2 番目の要素は 4 つの隣接セルの状態 (上、下、左、右) の合計を取り、それを別のスカラー量で掛けます。これは結合定数 ( J ) に似ています。乱数ジェネレーター ( r ) は、平均がゼロで標準偏差が固定の正規分布の値の範囲 ( r _σ ) で、これもスカラー定数 ( X ) で掛けられます。ネットの力 ( F ) の 3 つの要素のうち、隣接要素とランダム要素は正と負の値を生成できますが、外力は正のみで、時間の経過とともに支配的な力になるシステムには順方向バイアスが適用されます。

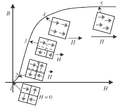
セルにかかるネットの力が正の場合、セルはオン (+1) になり、セルにかかる力が負の場合、セルはオフ (-1) になります。2D システムでは、さまざまな状態の組み合わせと配置が可能ですが、これは 3 つの領域、つまりすべて +1 またはすべて -1 の 2 つのグローバル安定状態と、両方の状態が混在する中間の不安定状態に分類できます。伝統的に、システムが不安定な場合はすぐにグローバル状態の 1 つに切り替わりますが、完全な条件、つまり臨界点では、ネットの力のパラメーターがバランスしている場合にのみ維持できる 2 つのグローバル状態の間に準安定状態が形成されることがあります。マトリックスの境界条件は上から下、左から右に循環するため、コーナー セルの問題は大きなマトリックスを使用して否定できます。

パチパチ、パチパチ、ポンポン

システムが刺激に対していつ、どのように反応するかを記述する3つの記述があります。外部磁場と他の成分の差によって、システムがポップ音を発するかクラックル音を発するかが決まりますが、ランダム成分と隣接成分の弾性率が外部磁場よりもはるかに大きい場合、システムは密度ゼロに急激に変化し、その後、変換速度が低下します。

${\displaystyle {\begin{aligned}Kt<{}&|X2r_{\sigma }-\Sigma JS|\Rightarrow {\text{ポッピング}}\\Kt>{}&|X2r_{\sigma }-\Sigma JS|\Rightarrow {\text{パチパチ}}\Rightarrow {\text{スナップ}}\\Kt\ll {}&|X2r_{\sigma }-\Sigma JS|\Rightarrow {\text{平衡状態へのスナップ}}\end{aligned}}}$

ポッピングとは、システムに対して可逆的で、システム全体の状態にほとんど影響を与えない小さな摂動が生じた状態です。

スナップとは、大規模なセルクラスターまたはシステム全体が別の状態、つまりすべて+1またはすべて-1に反転することです。システム全体が反転するのは、臨界点または転換点に達したときのみです。

パチパチという音は、システム内で可逆的な大小のクラスターが弾けたりパチパチと音を立てたりするときに観測されます。システムは常に不均衡な状態にあり、平衡状態に到達しようとしますが、内的または外的な力によって不可能になります。

コンポーネントの物理的な意味

ランダム成分（r）

地震をシミュレーションすることで、グーテンベルク・リヒターの法則を観察することが可能です。このシステムでは、ランダム成分は地面と空気のランダムな擾乱を表し、激しい気象システム、川の流れ、海岸に打ち寄せる波などの自然の連続的な刺激、掘削などの人間活動など、あらゆるものが対象となります。これはバタフライ効果によく似ており、ある事象の将来の結果を予測することも、シミュレーション中の特定の時点から元の状態を遡ることもできません。マクロレベルでは取るに足らないように見えますが、ミクロレベルでは連鎖反応を引き起こした可能性があります。つまり、1つの細胞のスイッチがオンになったことで、システム全体がオンになった可能性があります。

近傍成分（Σ S）

岩石やプレートなどの物理的な物体の隣接要素は、単にニュートンの運動の法則を説明したもので、プレートが移動して別のプレートと衝突すると、もう一方のプレートは反作用の力を提供します。同様に、大量の遊離粒子（岩、断層）が隣接する粒子に押し付けられると、隣接する粒子/物体も移動します。

外力（K）

外力とは、プレートの長期的な動き、あるいは上部マントル内の液体の岩石流であり、これらは継続的に作用する力です。最終的にはプレートが跳ね返ったり、破壊したりして、システムにかかる応力が軽減され、安定状態（すなわち地震）へと転じます。火山も同様で、地下のマグマの圧力が高まり、最終的には上部の乾燥した岩石層を圧倒して噴火を引き起こします。このようなモデルは、活動地域における地震や火山の発生を予測し、大規模な地震の後によく見られる余震を予測するために使用できます。

実用的な応用

磁石の磁化中、外部場は印加電界、隣接成分は双極子の局所的磁場の影響、ランダム成分は外部または内部刺激によるその他の摂動を表します。これには多くの実用的な用途があり、メーカーはこのタイプのシミュレーションを使用して磁石を非破壊的にテストし、特定の条件下でどのように反応するかを確認できます。ハンマーで叩いたり、床に落としたりなど、大きな力がかかった後の磁化をテストするには、外力 ( H ) または結合定数 ( J ) を突然増加させる可能性があります。熱条件をテストするには、熱変動の増加 ( X の増加) とともに 1 つのエッジに境界条件を適用できますが、これには 3 次元モデルが必要になります。

ビジネス界

株価の動向は普遍性を示している。ある企業の株価の過去のデータ^{[ 12 ]}を用いて日次リターンを計算し、それをヒストグラムにプロットすると、非ガウス分布のファットテール分布が得られる。株価は常に小さな変動を伴って変動し、大きな変動ははるかに稀である。証券取引所は、需給バランスに合わせて株価を調整することで、株価を均衡させる力として解釈できる。

小規模な企業、特に不安定な新興企業が定期的に設立される企業合併は、一定期間存続すれば成長を続ける可能性が高く、十分な規模に達すると他の小規模企業を買収して自社の規模を拡大することができます。これは、大企業が自社の市場シェア拡大のために競合他社を買収し、市場が飽和状態になるまでこれを繰り返すのとよく似ています。

自然界における例

現実世界では、システムの状態に影響を与える外的要因が多すぎるため、システムが永続的な平衡状態を維持することは不可能です。システムは一時的な平衡状態にあり、その後何らかの刺激によって突然機能不全に陥るか、あるいはシステムのバランスを取ろうとする外的要因によって常に位相が変化し続けるかのいずれかです。これらのシステムでは、ポンポンという音、パチパチという音、そしてパチパチという音が観察されます。

太陽黒点数の時系列データ。NOAAのデータセット。1945年1月1日から2017年6月30日まで。各日の黒点数は、その振幅を持つ0.01秒の音声パルスに変換されます。

• 
  紙をくしゃくしゃにするとパチパチという音がする。^{[ 2 ]}
• 
  地震のマグニチュードの関数としての地震の頻度（グーテンベルク・リヒターの法則）。
• 
  強磁性棒のドメインが外部磁場に整列する速度により、バルクハウゼン効果が生じます。
• 
  トウモロコシが弾ける音はパチパチという音ではなく、ポップ音の一種である。^{[ 5 ]}
• 
  過剰な積雪による雪崩の大きさの分布は数桁にわたります。^{[ 13 ]}
• 
  木材の非弾性的な機械的性質により鉛筆が折れる現象は、パチパチ音ではなく、折れる音の一例である。^{[ 5 ]}
• 
  土砂崩れの分布は、モグラ塚の崩壊から山腹の崩壊まで、パチパチという音を立てます。
• 
  火山は、内部のマグマ流の圧力が封印を超えると、最終的に噴火します。
• 
  ファンデルワールス力は、水面に形成される脂肪球が互いに引き寄せ合って自由エネルギーを減らし、より大きなクラスターになることを意味する。
• 
  牛乳を加えると、パフライスはパチパチと音を立てます。

参照

• インパルスノイズ
• ざわめき音
• クリック（音響）

参考文献

1. 「神秘的なパターンで数学と自然が融合 | Quanta Magazine」 www.quantamagazine.org 2013年2月5日。 2015年9月6日時点のオリジナルよりアーカイブ。 2016年11月27日閲覧。
2. Houle, Paul A.; Sethna, James P. (1996-07-01). 「紙をくしゃくしゃにしたときの音響放射」. Physical Review E. 54 ( 1): 278– 283. arXiv : cond-mat/9512055v1 . Bibcode : 1996PhRvE..54..278H . doi : 10.1103 /physreve.54.278 . ISSN 1063-651X . PMID 9965070. S2CID 14661751 .   
3. 「オペラ座の幽霊クリンクラーを沈黙させる望みはない」archive.nytimes.com . 2023年7月19日閲覧。
4. Kramer, Eric M.; Witten, Thomas A. (1997-02-17). 「圧縮弾性多様体における応力凝縮」 . Physical Review Letters . 78 (7): 1303– 1306. arXiv : cond-mat/9609037 . Bibcode : 1997PhRvL..78.1303K . doi : 10.1103/PhysRevLett.78.1303 . ISSN 0031-9007 . 
5. Sethna, James P.; Dahmen, Karin A.; Myers, Christopher R. (2001年3月). 「パチパチという音」 . Nature . 410 (6825): 242– 250. arXiv : cond-mat/0102091 . Bibcode : 2001Natur.410..242S . doi : 10.1038/35065675 . ISSN 1476-4687 . 
6. 「キュリー点 | 物理学」ブリタニカ百科事典. 2016年11月27日閲覧。
7. Schroder, Malte (2013). 「分数パーコレーションにおけるパチパチ音 – 爆発的パーコレーションにおけるランダムに分布する不連続ジャンプ」 . マックス・プランク動力学・自己組織化研究所.
8. 「強磁性のドメイン理論」 www.gitam.edu工学物理学科. 2016年11月20日時点のオリジナルよりアーカイブ。 2016年11月27日閲覧。
9. 「世界の地震情報」米国地質調査所、国立地震情報センター。 2008年3月28日時点のオリジナルよりアーカイブ。
10. Gutenberg, B. (1954). 『地球の地震活動と関連現象』 プリンストン：プリンストン大学出版局.
11. セスナ、ジェームズ.パチパチ音. 原子・固体物理学研究所、クラークホール、コーネル大学、イサカ、米国: マクミラン・マガジンズ社.
12. 「Yahoo Finance UK」 . Yahoo Finance UK . 2016年11月27日閲覧。
13. Birkeland, KW (2002). 「べき乗則と雪崩」 .地球物理学研究レターズ. 29 (11): 1554. Bibcode : 2002GeoRL..29.1554B . doi : 10.1029/2001GL014623 . ISSN 0094-8276 .