ダビドフ・ソリトン
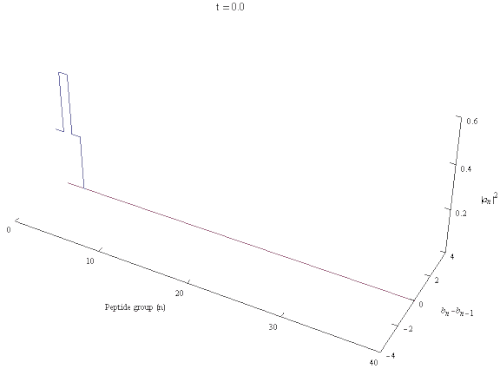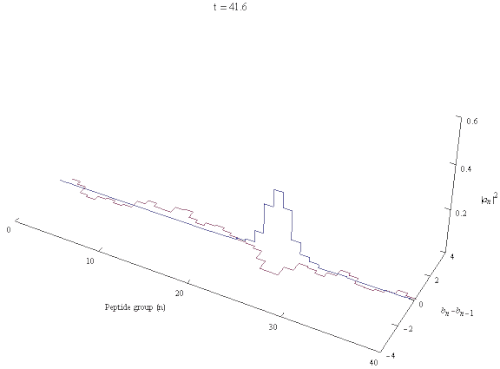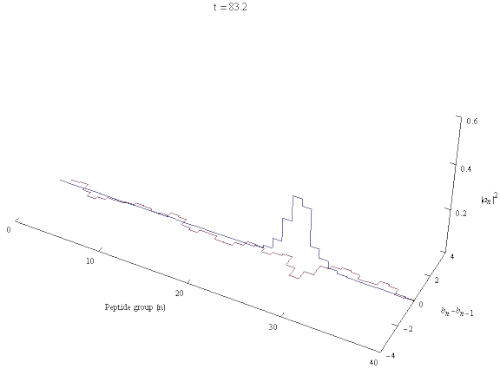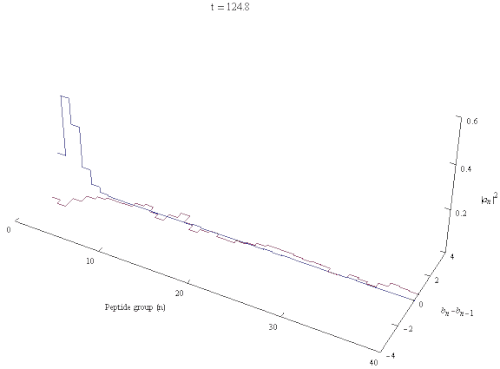
40個のペプチド基からなる単一のαヘリックススパインのN端（x軸に沿って伸びる）にある3つのペプチド基にわたるアミドIエネルギーの初期ガウスステップ分布によって125ピコ秒周期で生成されたpNのダビドフ・ソリトンの量子ダイナミクス。アミドI励起の量子確率はz軸に沿って青でプロットされている。フォノン格子変位差（ピコメートル単位で測定）はy軸に沿って赤でプロットされている。ソリトンは、誘起された格子歪みによるアミドIエネルギーの自己閉じ込めによって形成される。[ 1 ] [ 2 ]χ＝35{\displaystyle \χ =35}|あん|2{\displaystyle |a_{n}|^{2}}ばん−ばん−1{\displaystyle b_{n}-b_{n-1}}

量子生物学において、ダビドフ・ソリトン（ソビエトウクライナの物理学者アレクサンダー・ダビドフにちなんで名付けられた）は、タンパク質のαヘリックス内の自己捕捉アミドI基に沿って伝播する励起を表す準粒子である。これはダビドフ・ハミルトニアンの解である。

ダビドフモデルは、タンパク質のαヘリックスを安定化させる水素結合とアミドI振動との相互作用を記述する。αヘリックス内の基本励起は、格子の変形振動に対応するフォノンと、ペプチド基の内部アミドI励起を記述する励起子によって与えられる。タンパク質のαヘリックス領域の原子構造を参照すると、ダビドフソリトン（ポーラロン、励起子）が生成されるメカニズムは次のように記述できる。αヘリックス上に局在するC=O伸縮振動子（またはアミドI振動子）の振動エネルギーはフォノンカップリング効果を介してαヘリックスの構造を歪ませ、一方でヘリックス歪みはフォノンカップリングを介して再び反応し、アミドI振動エネルギーを捕捉してその分散を防ぐ。この効果は自己局在化または自己トラッピングと呼ばれる。[ 3 ] [ 4 ] [ 5 ]エネルギーが螺旋対称性を保つように分布するソリトンは動的に不安定であり、そのような対称ソリトンは伝播する際に急速に減衰する。一方、局所的な並進対称性と螺旋対称性を自発的に破る非対称ソリトンは、最も低いエネルギーを持ち、頑健な局所的実体である。[ 6 ]

ダヴィドフ・ハミルトニアン

ダヴィドフ・ハミルトニアンは、分極格子と電子の相互作用におけるフレーリッヒ・ホルシュタイン・ハミルトニアンと形式的には類似している。したがって、エネルギー演算子のハミルトニアンは H^{\displaystyle {\hat {H}}}

H^＝H^例+H^ph+H^int{\displaystyle {\hat {H}}={\hat {H}}_{\text{ex}}+{\hat {H}}_{\text{ph}}+{\hat {H}}_{\text{int}}}

ここで、 は励起子ハミルトニアンであり、隣接するサイト間のアミドI励起の運動を記述する。はフォノンハミルトニアンであり、格子の振動を記述する。 は相互作用ハミルトニアンであり、アミドI励起と格子の相互作用を記述する。[ 3 ] [ 4 ] [ 5 ]H^例{\displaystyle {\hat {H}}_{\text{ex}}}H^ph{\displaystyle {\hat {H}}_{\text{ph}}}H^int{\displaystyle {\hat {H}}_{\text{int}}}

励起子ハミルトニアンは ​H^例{\displaystyle {\hat {H}}_{\text{ex}}}

H^例＝∑ん、αE0A^ん、α†A^ん、α−J1∑ん、α（A^ん、α†A^ん+1、α+A^ん、α†A^ん−1、α）+J2∑ん、α（A^ん、α†A^ん、α+1+A^ん、α†A^ん、α−1）{\displaystyle {\begin{aligned}{\hat {H}}_{\text{ex}}=&\sum _{n,\alpha }E_{0}{\hat {A}}_{n,\alpha }^{\dagger }{\hat {A}}_{n,\alpha }\\&-J_{1}\sum _{n,\alpha }\left({\hat {A}}_{n,\alpha }^{\dagger }{\hat {A}}_{n+1,\alpha }+{\hat {A}}_{n,\alpha }^{\dagger }{\hat {A}}_{n-1,\alpha }\right)\\&+J_{2}\sum _{n,\alpha }\left({\hat {A}}_{n,\alpha }^{\dagger }{\hat {A}}_{n,\alpha +1}+{\hat {A}}_{n,\alpha }^{\dagger }{\hat {A}}_{n,\alpha -1}\right)\end{aligned}}}

ここで、添え字はαヘリックススパインに沿ったペプチドグループを数え、添え字は各αヘリックススパインを数え、z Jはアミド I 振動（CO 伸縮）のエネルギー、z Jは特定のアミド I 結合と同じスパインに沿った前後の結合との間の双極子-双極子結合エネルギー、 [ 7 ] z Jは特定のアミド I 結合とタンパク質α ヘリックスの同じ単位胞内の隣接するスパイン上の結合との間の双極子-双極子結合エネルギー、[ 7 ]およびはそれぞれペプチドグループにおけるアミド I 励起子のボソン生成および消滅演算子である。[ 8 ] [ 9 ] [ 10 ]ん＝1、2、⋯、N{\displaystyle n=1,2,\cdots,N}α＝1、2、3{\displaystyle \alpha =1,2,3}E0＝32.8{\displaystyle E_{0}=32.8}J1＝0.155{\displaystyle J_{1}=0.155}J2＝0.246{\displaystyle J_{2}=0.246}A^ん、α†{\displaystyle {\hat {A}}_{n,\alpha }^{\dagger }}A^ん、α{\displaystyle {\hat {A}}_{n,\alpha }}（ん、α）{\displaystyle (n,\alpha)}

フォノンハミルトニアンは[ 11 ] [ 12 ] [ 13 ] [ 14 ]​H^ph{\displaystyle {\hat {H}}_{\text{ph}}}

H^ph＝12∑ん、α[w1（u^ん+1、α−u^ん、α）2+w2（u^ん、α+1−u^ん、α）2+p^ん、α2Mん、α]{\displaystyle {\hat {H}}_{\text{ph}}={\frac {1}{2}}\sum _{n,\alpha }\left[w_{1}({\hat {u}}_{n+1,\alpha }-{\hat {u}}_{n,\alpha })^{2}+w_{2}({\hat {u}}_{n,\alpha +1}-{\hat {u}}_{n,\alpha })^{2}+{\frac {{\hat {p}}_{n,\alpha }^{2}}{M_{n,\alpha }}}\right]}

ここで、はペプチド基の平衡位置からの変位演算子、はペプチド基の運動量演算子、はペプチド基の質量、N / mは格子の有効弾性係数（水素結合のバネ定数）[ 9 ]であり、N / mはスパイン間の横方向結合である。[ 12 ] [ 15 ]u^ん、α{\displaystyle {\hat {u}}_{n,\alpha }}（ん、α）{\displaystyle (n,\alpha)}p^ん、α{\displaystyle {\hat {p}}_{n,\alpha }}（ん、α）{\displaystyle (n,\alpha)}Mん、α{\displaystyle M_{n,\alpha}}（ん、α）{\displaystyle (n,\alpha)}w1＝13−19.5{\displaystyle w_{1}=13-19.5}w2＝30.5{\displaystyle w_{2}=30.5}

最後に、相互作用ハミルトニアン は H^int{\displaystyle {\hat {H}}_{\text{int}}}

H^int＝χ∑ん、α[（u^ん+1、α−u^ん、α）A^ん、α†A^ん、α]{\displaystyle {\hat {H}}_{\text{int}}=\chi \sum _{n,\alpha }\left[({\hat {u}}_{n+1,\alpha }-{\hat {u}}_{n,\alpha }){\hat {A}}_{n,\alpha }^{\dagger }{\hat {A}}_{n,\alpha }\right]}

ここでpNは励起子と格子変位（フォノン）との結合から生じる非調和パラメータであり、励起子-フォノン相互作用の強さをパラメータ化する。[ 9 ] αヘリックスに対するこのパラメータの値は、理論的に計算された吸収線の形状と実験的に測定されたものとの比較によって決定された。 χ＝35−62{\displaystyle \chi =35-62}

ダビドフ・ソリトンの性質

ダビドフ・ハミルトニアンから運動方程式を導くための基本的なアプローチは3つあります

ダヴィドフソリトンを解析するために使用される数学的手法は、ポーラロン理論で開発されたものと類似している。[ 18 ]この文脈では、ダヴィドフソリトンは次の ポーラロンに対応する。

  • 大きいので連続体極限近似が正当化される、[ 9 ]
  • 音響的自己局在は格子の音響モードとの相互作用から生じるため、[ 9 ]
  • 非調和エネルギーはフォノン帯域幅に比べて小さいため、弱結合している。 [ 9 ]

ダヴィドフ・ソリトンは量子準粒子であり、ハイゼンベルクの不確定性原理に従う。したがって、並進不変性を課さないモデルは、その構成に欠陥がある。[ 9 ]ダヴィドフ・ソリトンがαヘリックスの5回転に局在すると仮定すると、ソリトンの速度（m/s）に大きな不確定性が生じるが、ダヴィドフ・ソリトンを古典的な物体としてモデル化すると、この事実は不明瞭になる。 Δv＝133{\displaystyle \Delta v=133}

参考文献

  1. ^ Georgiev, Danko D.; Glazebrook, James F. (2019). 「タンパク質αヘリックスにおけるダビドフ・ソリトンの量子ダイナミクスについて」. Physica A: 統計力学とその応用. 517 : 257–269 . arXiv : 1811.05886 . Bibcode : 2019PhyA..517..257G . doi : 10.1016/ j.physa.2018.11.026 . MR  3880179. S2CID 53688720 
  2. ^ Georgiev, Danko D.; Glazebrook, James F. (2019). 「質量障壁を通過するダヴィドフソリトンの量子トンネル効果」.カオス、ソリトン、フラクタル. 123 : 275–293 . arXiv : 1904.09822 . Bibcode : 2019CSF...123..275G . doi : 10.1016/ j.chaos.2019.04.013 . MR 3941070. S2CID 128306516 .  
  3. ^ a b Davydov, Alexander S. (1973). 「励起下におけるタンパク質の収縮理論」. Journal of Theoretical Biology . 38 (3): 559– 569. Bibcode : 1973JThBi..38..559D . doi : 10.1016/0022-5193(73)90256-7 . PMID 4266326 . 
  4. ^ a b Davydov, Alexander S. (1977). 「ソリトンとタンパク質分子に沿ったエネルギー移動」. Journal of Theoretical Biology . 66 (2): 379– 387. Bibcode : 1977JThBi..66..379D . doi : 10.1016/0022-5193(77)90178-3 . PMID 886872 . 
  5. ^ a b Davydov, Alexander S. (1979). 「ソリトン、生体エネルギー、そして筋収縮のメカニズム」. International Journal of Quantum Chemistry . 16 (1): 5– 17. doi : 10.1002/qua.560160104 .
  6. ^ Brizhik, Larissa; Eremko, Alexander; Piette, Bernard; Zakrzewski, Wojtek (2004). 「αヘリカルタンパク質におけるソリトン」. Physical Review E. 70 ( 3 Pt 1): 031914. arXiv : cond-mat/0402644 . Bibcode : 2004PhRvE..70a1914K . doi : 10.1103/PhysRevE.70.011914 . PMID 15524556 . 
  7. ^ a b Nevskaya, NA; Chirgadze, Yuriy Nikolaevich (1976). 「α-ヘリックスのアミドIおよびII振動の赤外線スペクトルと共鳴相互作用」. Biopolymers . 15 ( 4): 637– 648. doi : 10.1002/bip.1976.360150404 . PMID 1252599. S2CID 98650911 .  
  8. ^ Hyman, James M.; McLaughlin, David W.; Scott, Alwyn C. (1981). 「ダヴィドフのαヘリックスソリトンについて」. Physica D: 非線形現象. 3 (1): 23– 44. Bibcode : 1981PhyD....3...23H . doi : 10.1016/0167-2789(81)90117-2 .
  9. ^ a b c d e f g Scott, Alwyn C. (1992). 「ダヴィドフのソリトン」. Physics Reports . 217 (1): 1– 67. Bibcode : 1992PhR...217....1S . doi : 10.1016/0370-1573(92)90093-F .
  10. ^ a b Cruzeiro-Hansson, Leonor; Takeno, Shozo (1997). 「ダヴィドフ模型：量子系、量子古典混合系、完全古典系」. Physical Review E. 56 ( 1): 894– 906. Bibcode : 1997PhRvE..56..894C . doi : 10.1103/PhysRevE.56.894 .
  11. ^ Davydov, Alexander S. (1982). 「準1次元分子構造におけるソリトン」.ソビエト物理学誌25 ( 12): 898– 918. doi : 10.1070/pu1982v025n12abeh005012 .
  12. ^ a b Georgiev, Danko D.; Glazebrook, James F. (2022). 「タンパク質αヘリックスにおけるソリトンの熱安定性」.カオス、ソリトン、フラクタル. 155 111644. arXiv : 2202.00525 . Bibcode : 2022CSF...15511644G . doi : 10.1016/ j.chaos.2021.111644 . MR 4372713. S2CID 244693789 .  
  13. ^ Zolotaryuk, Alexander V.; Christiansen, PL; Norden, B.; Savin, Alexander V. (1999). 「螺旋におけるソリトンとラチェット運動」 .凝縮系物理学. 2 (2): 293– 302. Bibcode : 1999CMPh....2..293Z . doi : 10.5488/cmp.2.2.293 .
  14. ^ Brizhik, Larissa S.; Luo, Jingxi; Piette, Bernard MAG; Zakrzewski, Wojtek J. (2019). 「αヘリックスを介した長距離ドナー-アクセプター電子輸送」. Physical Review E. 100 ( 6) 062205. arXiv : 1909.08266 . Bibcode : 2019PhRvE.100f2205B . doi : 10.1103/ PhysRevE.100.062205 . PMID 31962511. S2CID 202660869 .  
  15. ^ Savin, Alexander V.; Zolotaryuk, Alexander V. (1993). 「分子鎖におけるアミドI励起の熱音響・光モードによるダイナミクス」. Physica D: Nonlinear Phenomena . 68 (1): 59– 64. Bibcode : 1993PhyD...68...59S . doi : 10.1016/0167-2789(93)90029-Z .
  16. ^ Kerr, William C.; Lomdahl, Peter S. (1987). 「ダヴィドフ・ソリトンの運動方程式の量子力学的導出」. Physical Review B. 35 ( 7): 3629– 3632. Bibcode : 1987PhRvB..35.3629K . doi : 10.1103/PhysRevB.35.3629 . hdl : 10339/15922 . PMID 9941870 . 
  17. ^ Škrinjar, MJ; Kapor, DV; Stojanović, SD (1988). 「ダヴィドフのソリトン理論への古典的および量子的アプローチ」. Physical Review A. 38 ( 12): 6402– 6408. Bibcode : 1988PhRvA..38.6402S . doi : 10.1103/PhysRevA.38.6402 . PMID 9900400 . 
  18. ^ Sun, Jin; Luo, Bin; Zhao, Yang (2010). 「Davydov ansätze による1次元ホルスタイン・ポーラロンのダイナミクス」. Physical Review B. 82 ( 1) 014305. arXiv : 1001.3198 . Bibcode : 2010PhRvB..82a4305S . doi : 10.1103/PhysRevB.82.014305 . S2CID 118564115 . 
「 https://en.wikipedia.org/w/index.php?title=Davydov_soliton&oldid=1330826804」より取得