折れ線グラフ
数学の分野であるグラフ理論では、無向グラフGの線グラフは、 Gの辺間の隣接関係を表す別のグラフ L( G )です。 L( G )は次のように構築されます。Gの各辺に対して、 L( G )に頂点を作成します 。 Gで共通の頂点を持つ 2 つの辺ごとに、 L( G )の対応する頂点間に辺を作成します 。
線グラフという名称は、Harary & Norman (1960)の論文に由来するが、 Whitney (1932)とKrausz (1943)の両者は、これ以前にもこの構成を使用していた。[ 1 ]線グラフに使用される他の用語には、被覆グラフ、導関数、辺頂点双対、共役、代表グラフ、θ-オブラゾム[ 1 ]、およびエッジグラフ、交換グラフ、随伴グラフ、導出グラフなどがある。[ 2 ]
ハスラー・ホイットニー (1932 )は、例外的なケースを1つ除き、連結グラフGの構造をその線グラフから完全に復元できることを証明した。[ 3 ]線グラフの他の多くの特性は、基礎となるグラフの特性を頂点から辺へ変換することによって得られ、ホイットニーの定理により、同じ変換を逆方向にも行うことができる。線グラフはクローフリーであり、二部グラフの線グラフはパーフェクトである。線グラフは9つの禁制部分グラフによって特徴付けられ、線形時間で認識することができる。
線グラフの概念のさまざまな拡張が研究されており、線グラフの線グラフ、マルチグラフの線グラフ、ハイパーグラフの線グラフ、重み付きグラフの線グラフなどがあります。
正式な定義
グラフGが与えられたとき、その線グラフL ( G )は次のようなグラフである。
つまり、これはGの辺の交差グラフであり、各辺はその2つの端点の集合によって表される。[ 2 ]
例
以下の図は、グラフ(左、青い頂点)とその折れ線グラフ(右、緑の頂点)を示しています。折れ線グラフの各頂点には、元のグラフの対応する辺の端点のペアがラベル付けされています。例えば、右側の緑の頂点「1,3」は、左側の青い頂点「1」と「3」の間の辺に対応しています。緑の頂点「1,3」は、他の3つの緑の頂点「1,4」と「1,2」(青いグラフの端点「1」を共有する辺に対応)と「4,3」(青いグラフの端点「3」を共有する辺に対応)に隣接しています。
- グラフG
- Gの辺から構成されるL( G )の頂点
- L( G )に追加されたエッジ
- 折れ線グラフL( G )
プロパティ
基礎となるグラフの翻訳されたプロパティ
グラフGにおいて辺の隣接性のみに依存する性質は、グラフ L ( G )において頂点の隣接性に依存する性質に翻訳できる。例えば、Gにおけるマッチングとは、どの辺も隣接していない辺の集合であり、これはL ( G )におけるどの頂点も隣接していない頂点の集合、すなわち独立集合に対応する。[ 4 ]
したがって、
- 連結グラフの線グラフは連結である。Gが連結である場合、Gの任意の2辺を結ぶパスが存在し、これはL ( G )の任意の2頂点を含むL ( G )のパスとなる。しかし、グラフGに孤立した頂点がいくつかあり、したがって連結されていない場合でも、連結線グラフが存在することがある。[ 5 ]
- 線グラフが連結点を持つのは、そのグラフの両端の線分が1次でない橋を持つ場合に限られます。[ 2 ]
- n個の頂点とm個の辺を持つグラフGの場合、線グラフL ( G )の頂点の数はmであり、 L ( G )の辺の数はGの頂点の次数の二乗の和の半分からmを引いた値である。[ 6 ]
- L ( G ) の独立集合はGのマッチングに対応する。特に、L ( G )の最大独立集合はGの最大マッチングに対応する。最大マッチングは多項式時間で見つけることができるため、線グラフの最大独立集合も、より一般的なグラフ族の最大独立集合問題が困難であるにもかかわらず、多項式時間で見つけることができる。[ 4 ]同様に、L ( G )のレインボー独立集合はGのレインボーマッチングに対応する。
- グラフGの辺彩色数は、その線グラフL ( G )の頂点彩色数に等しい。[ 7 ]
- 辺推移グラフの線グラフは頂点推移的である。この性質は、(ピーターセングラフのように)頂点推移的だがケイリーグラフではないグラフの族を生成するために使用できる。例えば、Gが少なくとも5つの頂点を持ち、二部グラフではなく、頂点次数が奇数である辺推移グラフである場合、L ( G )は頂点推移的な非ケイリーグラフである。[ 8 ]
- グラフGがオイラー閉路を持つ場合、つまりGが連結で各頂点に偶数個の辺を持つ場合、Gの線グラフはハミルトン閉路である。しかし、線グラフのハミルトン閉路のすべてがこのようにオイラー閉路から生じるわけではない。例えば、ハミルトングラフGの線グラフは、 Gがオイラーグラフであるかどうかに関わらず、それ自体がハミルトン閉路である。[ 9 ]
- 2つの単純グラフが同型であれば、それらの線グラフも同型である。ホイットニーグラフ同型定理は、連結グラフの1組を除くすべての組に対して、この逆定理を与える。
- 複雑ネットワーク理論の文脈では、ランダムネットワークの線グラフは、スモールワールド特性(すべての頂点ペアの間に短いパスが存在する)や次数分布の形状など、ネットワークの多くの特性を保持します。[ 10 ] EvansとLambiotte(2009)は、複雑ネットワークで頂点クラスターを見つけるための任意の方法を線グラフに適用して、代わりにそのエッジをクラスター化するために使用できることを指摘しています。
ホイットニー同型定理

二つの連結グラフの線グラフが同型であれば、その基となるグラフも同型である。ただし、三角形グラフK 3とクローグラフK 1,3は線グラフは同型だが、それ自体は同型ではない。[ 3 ]
K 3やK 1,3の他にも、線グラフの対称性がグラフ自体よりも高いという特性を持つ例外的な小グラフがいくつかあります。例えば、ダイヤモンドグラフK 1,1,2(2つの三角形が1つの辺を共有)には4つのグラフ自己同型がありますが、その線グラフK 1,2,2には8つの自己同型があります。示されているダイヤモンドグラフの図では、グラフを90度回転することはグラフの対称性ではなく、線グラフの対称性です。ただし、このような例外的なケースはすべて、最大で4つの頂点を持ちます。ホイットニー同型定理の強化版は、4つ以上の頂点を持つ連結グラフの場合、グラフの同型性と線グラフの同型性の間には1対1の対応があると述べています。[ 11 ]
ホイットニー同型定理の類似物は多重グラフの線グラフに対しても証明されているが、この場合はより複雑である。[ 12 ]
強規則性と完全性を持つ折れ線グラフ

完全グラフK nの線グラフは、三角グラフ、ジョンソングラフJ ( n , 2)、またはクネザーグラフKG n ,2の補グラフとしても知られています。三角グラフは、 n = 8を除いて、スペクトルによって特徴付けられます。[ 13 ]これらはまた、パラメータsrg( n ( n − 1 )/2, 2( n − 2 ), n − 2, 4)を持つ強力に正則なグラフとして特徴付けられることもあります (これもK 8 を除きます) 。[ 14 ] L ( K 8 )と同じパラメータとスペクトルを持つ 3 つの強力に正則なグラフは、 L ( K 8 )からのグラフ切り替えによって得られるチャングラフです。
二部グラフの折れ線グラフは完全グラフである(ケーニヒの定理を参照) が、クローグラフの例が示すように二部グラフである必要はない。二部グラフの折れ線グラフは、完全グラフの重要な構成要素の 1 つであり、強い完全グラフ定理の証明に使用されている。[ 15 ]これらのグラフの特殊なケースは、ルークのグラフ、つまり完全二部グラフの折れ線グラフである。完全グラフの折れ線グラフと同様に、これらは 1 つの例外を除いて、頂点の数、辺の数、隣接点と非隣接点の共有近傍の数によって特徴付けることができる。唯一の例外ケースはL ( K 4,4 )であり、これはシュリカンデ グラフとパラメータを共有する。二分割の両側に同じ数の頂点がある場合、これらのグラフも強正則である。[ 16 ] C 3、 C 4、 C 5を除いて、すべての連結された強正則グラフは、2つの線グラフ変換内で非強正則にできることが示されている 。 [ 17 ]連結されていないグラフへの拡張では、グラフがC 3の互いに素な和集合ではないことが必要となる 。
より一般的には、グラフGはL ( G )が完全グラフであるとき、線完全グラフであると言われる。線完全グラフとは、3より大きい奇数長さの単純閉路を含まないグラフのことである。 [ 18 ]同様に、グラフが線完全であるためには、その2連結成分のそれぞれが2部グラフであるか、 K 4(正四面体)またはK 1,1, n(共通の辺を共有する1つ以上の三角形の組)のいずれかの形をとる必要がある。 [ 19 ]すべての線完全グラフはそれ自体が完全である。[ 20 ]
その他の関連グラフファミリー
すべての線グラフはクローフリーグラフであり、3葉木の形の誘導サブグラフを持たないグラフです。 [ 21 ]より一般的なクローフリーグラフと同様に、偶数個のエッジを持つすべての接続された線グラフL ( G )は完全マッチングを持ちます。[ 22 ]同様に、これは、基礎となるグラフGに偶数個のエッジがある場合、そのエッジを2エッジパスに分割できることを意味します。
木の線グラフはまさに爪のないブロックグラフである。[ 23 ]これらのグラフは極値グラフ理論における問題を解決するために使われてきた。その問題は、与えられた数の辺と頂点を持つグラフを構築し、その部分グラフとして誘導される最大の木が可能な限り小さくなるようにすることである。[ 24 ]
線グラフの隣接行列Aの固有値はすべて少なくとも-2である。これは、Aがと書けるためである。ここで、Jは線グラフ前の符号なし接続行列であり、Iは単位行列である。特に、A + 2 Iはベクトル系のグラミアン行列である。この性質を持つすべてのグラフは、一般化線グラフと呼ばれている。[ 25 ]
特性評価と認識
クリーク分割

任意のグラフGとG内の任意の頂点vに対して、 vに接続する辺の集合は線グラフL ( G )内のクリークに対応する。このようにして形成されたクリークはL ( G )の辺を分割する。 L ( G )の各頂点は、これらのクリークのうちのちょうど2つ( G内の対応する辺の2つの端点に対応する2つのクリーク)に属する。
このようなクリークへの分割の存在は、線グラフを特徴付けるために使用できます。グラフLが他のグラフまたはマルチグラフの線グラフである場合、Lの各頂点がちょうど 2 つのクリークに属するように、 Lの辺を分割するクリークのコレクション (一部のクリークは単一の頂点である可能性がある) を見つけることができる場合のみです。 [ 21 ]このクリークの集合が、 Lの2 つの頂点が両方とも同じ 2 つのクリークに存在しないという追加条件を満たす場合、それはグラフの線グラフ (マルチグラフではなく) です。このようなクリークのファミリーが与えられた場合、各クリークに対してGの1 つの頂点を作成し、 L の各頂点に対してGの辺を作成し、その端点がLの頂点を含む 2 つのクリークになるようにすることで、Lが線グラフである基礎となるグラフGを復元できます。ホイットニーの同型定理の強いバージョンによれば、基礎となるグラフGに 4 つ以上の頂点がある場合、このタイプのパーティションは 1 つしか存在できません。
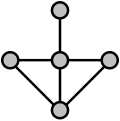
たとえば、この特徴付けは、次のグラフが折れ線グラフではないことを示すために使用できます。
この例では、中央の次数4の頂点から上、左、右に伸びる辺には共通のクリークがありません。したがって、グラフの辺をクリークに分割する場合、これらの3つの辺それぞれに少なくとも1つのクリークが存在する必要があり、これらの3つのクリークはすべて中央の頂点で交差するため、「各頂点は必ず2つのクリークに出現する」という要件に違反します。したがって、このグラフは線グラフではありません。
禁制部分グラフ

線グラフの別の特徴づけはBeineke (1970)で証明された(そしてBeineke (1968)によって証明なしに以前に報告されていた)。彼は、線グラフではない極小グラフが 9 個存在し、線グラフではない任意のグラフはこれら 9 個のグラフのいずれかを誘導部分グラフとして持つことを示した。つまり、グラフが線グラフである場合は、その頂点の部分集合がこれら 9 個のグラフのいずれかを誘導しないときのみである。上の例では、最上位の 4 個の頂点がクロー(つまり、完全二部グラフK 1,3)を誘導し、これは禁制部分グラフの図の左上に表示されている。したがって、Beineke の特徴づけによれば、この例は線グラフではない。最小次数が 5 以上のグラフの場合、図の左列と右列の 6 個の部分グラフのみが特徴づけに必要なものである。[ 26 ]
アルゴリズム
Roussopoulos (1973)とLehot (1974) は、線グラフを認識し、元のグラフを再構築するための線形時間アルゴリズムを説明しました。Sysło (1982) は、これらの手法を有向グラフに一般化しました。Degiorgiと Simon (1995)は、頂点の挿入と削除を前提とした動的グラフを維持し、各ステップで変更されたエッジの数に比例する時間で、入力を線グラフ(存在する場合)として表現するための効率的なデータ構造を説明しました。
Roussopoulos (1973)とLehot (1974)のアルゴリズムは、奇数三角形(奇数個の三角形の頂点に隣接する別の頂点が存在するという性質を持つ折れ線グラフ)を含む折れ線グラフの特徴付けに基づいています。一方、Degiorgi & Simon (1995)のアルゴリズムは、Whitney の同型定理のみを使用しています。このアルゴリズムは、グラフが折れ線グラフになる原因となる削除を認識する必要があるため複雑ですが、静的認識問題に特化すれば挿入のみを実行すればよく、アルゴリズムは以下の手順を実行します。
- 入力グラフL を、頂点を一つずつ追加することで構築する。各ステップでは、追加する頂点として、既に追加した頂点に少なくとも一つ隣接する頂点を選択する。Lに頂点を追加している間、 L = L ( G )となるグラフGを維持する。アルゴリズムが適切なグラフGを見つけられなかった場合、入力は線グラフではないため、アルゴリズムは終了する。
- グラフL ( G )に頂点vを追加する場合、 Gの頂点数が4つ以下であれば、線グラフ表現が一意にならない可能性があります。しかし、この場合、拡張グラフは十分に小さいため、線グラフとしての表現は総当たり探索によって定数時間で見つけることができます。
- より大きなグラフLに頂点vを追加する場合、そのグラフは別のグラフGの線グラフに等しい。Sは、 Lにおけるvの隣接頂点に対応する辺によって形成されるGのサブグラフとする。Sが、1つの頂点または隣接しない2つの頂点からなる頂点カバーを持つことを確認する。カバー内に2つの頂点がある場合、これらの2つの頂点を結ぶ辺(vに対応する)を追加してGを拡張する。カバー内に1つの頂点しかない場合、その頂点に隣接する新しい頂点をGに追加する。
各ステップは定数時間を要するか、グラフS内の一定サイズの頂点被覆(そのサイズはvの近傍数に比例する)を見つける処理を伴う。したがって、アルゴリズム全体の合計時間は、すべての頂点の近傍数の合計に比例し、これは(ハンドシェイクの補題により)入力辺の数に比例する。
折れ線グラフ演算子の反復
van Rooij & Wilf (1965)はグラフの順序を考察
彼らは、G が有限連結グラフである場合、このシーケンスでは 4 つの動作のみが可能であると示しています。
- Gがサイクルグラフである場合、L ( G )およびこのシーケンス内の後続の各グラフはG自身と同型である。これらは、 L ( G )がGと同型となる唯一の連結グラフである。[ 27 ]
- Gが爪K 1,3の場合、L ( G )およびシーケンス内の後続のすべてのグラフは三角形になります。
- Gがパス グラフである場合、シーケンス内の後続の各グラフは、最終的にシーケンスが空のグラフで終了するまで、より短いパスになります。
- 残りのすべてのケースでは、このシーケンス内のグラフのサイズは最終的に無制限に増加します。
Gが接続されていない場合、この分類はGの各コンポーネントに個別に適用されます。
パスではない連結グラフの場合、線グラフ操作の反復回数が十分に多いと、ハミルトングラフが生成される。[ 28 ]
一般化
中位グラフと凸多面体
平面グラフG の最大頂点次数が3のとき、その線グラフは平面グラフであり、Gのすべての平面埋め込みはL ( G )の埋め込みに拡張できる。しかし、より高次の平面グラフであっても線グラフが非平面となるものがある。これには、例えば、5つ星K 1,5、正五角形内に2つの交差しない対角線を追加して形成される宝石グラフ、および次数4以上の頂点を持つすべての凸多面体などが含まれる。[ 29 ]
代替構成である中間グラフは、最大次数3の平面グラフの線グラフと一致するが、常に平面的である。中間グラフは線グラフと同じ頂点を持つが、辺の数は少なくなる可能性がある。中間グラフの2つの頂点が隣接するのは、対応する2つの辺が平面埋め込みの何らかの面上で連続している場合に限る。平面グラフの双対グラフの中間グラフは、元の平面グラフの中間グラフと同じである。[ 30 ]
正多面体や単純多面体の場合、中線グラフ演算は、多面体の各頂点を、そのすべての辺の中点を通る平面で切断する演算によって幾何学的に表現できます。[ 31 ]この演算は、第2切断、[ 32 ]退化切断、[ 33 ]または整流化など、さまざまな呼び方で知られています。[ 34 ]
合計グラフ
グラフGの全体グラフT ( G )は、 Gの要素(頂点または辺)を頂点とし、2つの要素が隣接または接続している場合には必ず辺を持つ。全体グラフは、 Gの各辺を細分化し、細分化したグラフの平方をとることによっても得られる。 [ 35 ]
マルチグラフ
Gの線グラフの概念は、Gが多重グラフの場合にも自然に拡張できる。この場合、これらのグラフの特徴付けは簡略化できる。クリーク分割による特徴付けでは、2つの頂点が同じクリークに属することを防ぐ必要がなくなり、禁制グラフによる特徴付けでは、禁制グラフの数が9個ではなく7個となる。[ 36 ]
しかし、多重グラフの場合、同じ線グラフを持つ非同型グラフのペアはより多く存在します。例えば、完全二部グラフK 1, nは、双極子グラフやシャノン多重グラフと同じ辺数を持つ線グラフを持ちます。それでもなお、この場合にもホイットニーの同型定理との類似性を導くことができます。[ 12 ]
線分有向グラフ

線グラフを有向グラフに一般化することもできる。[ 37 ] Gが有向グラフである場合、その有向線グラフまたは線有向グラフはGの各辺に対して1つの頂点を持つ。Gにおけるuからvおよびwからxへの有向辺を表す2つの頂点は、v = wのとき、線有向グラフにおいてuvからwxへの辺で接続される。つまり、Gの線有向グラフの各辺はG内の長さ2の有向パスを表す。ド・ブリュイン・グラフは、完全な有向グラフから始めて、この有向線グラフの形成プロセスを繰り返すことによって形成することができる。[ 38 ]
加重折れ線グラフ
折れ線グラフL ( G )では、元のグラフGの次数kの各頂点は、折れ線グラフにk ( k − 1)/2本のエッジを作成します。多くの種類の分析では、これはGの高次ノードが折れ線グラフL ( G )で過剰に表現されていることを意味します。たとえば、元のグラフGの頂点でのランダム ウォークを検討してください。これは、ある頻度fで何らかのエッジeに沿って通過します。一方、このエッジeは、折れ線グラフL ( G )内の一意の頂点、たとえばvにマップされます。ここで、折れ線グラフの頂点で同じ種類のランダム ウォークを実行すると、 vが訪問される頻度は、fとはまったく異なる場合があります。Gのエッジeが次数O ( k )のノードに接続されている場合、折れ線グラフL ( G )では、エッジ e はO ( k 2 )より頻繁にトラバースされます。言い換えれば、ホイットニーグラフ同型定理は、線グラフがほぼ常に元のグラフGの位相を忠実にエンコードすることを保証しますが、これら 2 つのグラフ上のダイナミクスが単純な関係を持つことは保証しません。 1 つの解決策は、重み付き線グラフ、つまり重み付きエッジを持つ線グラフを構築することです。これを行うにはいくつかの自然な方法があります。[ 39 ]たとえば、グラフGのエッジdとe が次数kの頂点vに接続されている場合、線グラフL ( G )では、2 つの頂点dとeを接続するエッジに重み1/( k − 1)を与えることができます。このようにして、Gのすべてのエッジ(どちらの端も次数 1 の頂点に接続されていないことを条件とします) は、線グラフL ( G )で、そのエッジがGで持つ 2 つの端に対応する強度 2 を持ちます。重み付き線グラフのこの定義を、元のグラフG有向グラフや重み付けグラフもありました。[ 40 ] 全てのケースにおいて原則となるのは、線グラフL ( G )が元のグラフGのトポロジーだけでなくダイナミクスも反映するようにすることです。
ハイパーグラフの線グラフ
ハイパーグラフのエッジは任意の集合の族を形成することがあるため、ハイパーグラフの線グラフはその族の集合の 交差グラフと同じになります。
分離グラフ
Gの分離グラフD ( G )は次のように構築されます。G の各辺に対して、D ( G )に頂点を作成します。G 内の共通の頂点を持たない2つの辺に対して、 D ( G )内の対応する頂点間に辺を作成します。[ 41 ]言い換えれば、D ( G )はL ( G )の補グラフです。D ( G )内のクリークはL ( G )内の独立集合に対応し、その逆も同様です。
注記
- ^ a bヘミンガー&ベイネケ(1978)、273ページ。
- ^ a b cハラリー (1972)、p. 71.
- ^ a b Whitney (1932) ; Krausz (1943) ; Harary (1972) 、定理8.3、p. 72。HararyはJung (1966)によるこの定理の簡略化された証明を与えている。
- ^ a b Paschos, Vangelis Th. (2010),組合せ最適化と理論計算機科学:インターフェースと展望, John Wiley & Sons, p. 394, ISBN 978-0-470-39367-3明らかに、
グラフのマッチングとその線グラフの独立集合の間には 1 対 1 の対応があります。
- ^線グラフの接続性を考慮する際に孤立した頂点を考慮する必要があることは、 Cvetković、Rowlinson、Simić(2004)、 p.32で指摘されています。
- ^ Harary (1972)、定理 8.1、p. 72.
- ^ Diestel, Reinhard (2006),グラフ理論, Graduate Texts in Mathematics, vol. 173, Springer, p. 112, ISBN 978-3-540-26183-4無料オンライン版では、第5章(「着色」)の118ページにも掲載されています。
- ^ Lauri, Josef; Scapellato, Raffaele (2003), Topics in graph automorphisms and reconstruction , London Mathematical Society Student Texts, vol. 54, Cambridge: Cambridge University Press, p. 44, ISBN 0-521-82151-7、MR 1971819Lauri と Scapellato はこの結果を Mark Watkins の功績だと考えています。
- ^ Harary (1972)、定理 8.8、p. 80.
- ^ラメザンプール、カリミプール、マシャギ (2003)。
- ^ユング (1966) ;デジョルジとサイモン (1995)。
- ^ a bズヴェロヴィッチ(1997)
- ^ van Dam, Edwin R.; Haemers, Willem H. (2003)、「スペクトルによって決定されるグラフはどれか?」線形代数とその応用、373 : 241– 272、doi : 10.1016/S0024-3795(03)00483-X、MR 2022290、S2CID 32070167 特に命題8(262ページ)を参照。
- ^ Harary (1972)、定理8.6、p. 79。Hararyはこの結果を、LC Chang (1959)とAJ Hoffman (1960)による独立した論文によるものとしている。
- ^マリア・チュドノフスキー、ニール・ロバートソン、ポール・シーモア、ロビン・トーマス(2006)、「強完全グラフ定理」、数学年報、164 (1): 51– 229、arXiv : math/0212070、doi : 10.4007/annals.2006.164.51、S2CID 119151552 . Roussel, F.; Rusu, I.; Thuillier, H. (2009)「強いパーフェクトグラフ予想:40年間の試みとその解決」、Discrete Mathematics、309 (20): 6092– 6113、doi : 10.1016/j.disc.2009.05.024、MR 2552645、S2CID 16049392も参照。 。
- ^ Harary (1972) , Theorem 8.7, p. 79. Hararyは、完全二部グラフの線グラフのこの特徴づけをMoonとHoffmanに帰している。両辺の頂点数が等しいケースは、既にShrikhandeによって証明されていた。
- ^ Yang, Fan; Huang, Xingyue (2024). 「グラフ学習における線グラフ変換に関する理論的考察」arXiv : 2410.16138 [ cs.LG ].
- ^トロッター (1977) ;デ・ウェラ (1978 )
- ^マフレー(1992年)。
- ^トロッター (1977) .
- ^ a b Harary (1972)、定理8.4、p. 74では、線グラフの3つの同等な特徴付けが示されています。それは、エッジをクリークに分割すること、クローフリーで奇数のダイヤモンドフリーである性質、およびBeinekeの9つの禁制グラフです。
- ^サムナー、デイビッド・P. (1974)、「1因子グラフ」、アメリカ数学会誌、42 (1)、アメリカ数学会: 8–12、doi : 10.2307/2039666、JSTOR 2039666、MR 0323648 。Las Vergnas, M. (1975)、「グラフのマッチングに関するメモ」、Cahiers du Centre d'Études de Recherche Opérationnelle、17 (2–3–4): 257– 260、MR 0412042 。
- ^ Harary (1972)、定理8.5、p. 78。Hararyはこの結果をGary Chartrandに帰している。
- ^エルデシュ, ポール;サックス, マイケル;ソス, ヴェラ T. (1986)、「グラフにおける最大誘導木」、Journal of Combinatorial Theory、シリーズB、41 (1): 61– 79、doi : 10.1016/0095-8956(86)90028-6。
- ^ツヴェトコビッチ、ローリンソン、シミッチ (2004)。
- ^メテルスキー&ティシュケビッチ(1997)
- ^この結果はHarary(1972)の定理8.2でもある。
- ^ Harary (1972)、定理8.11、p.81。Hararyはこの結果をGary Chartrandに帰した。
- ^セドラチェク (1964) ;グリーンウェルとヘミンジャー (1972)。
- ^アーチディーコン、ダン(1992)、「メディアルグラフと電圧-電流双対性」、離散数学、104(2):111-141、doi:10.1016/0012-365X(92)90328-D、MR 1172842 。
- ^ McKee, TA (1989), 「地理的双対性のグラフ理論的モデル」, Combinatorial Mathematics: Proceedings of the Third International Conference (New York, 1985) , Ann. New York Acad. Sci., vol. 555, New York: New York Acad. Sci., pp. 310– 315, Bibcode : 1989NYASA.555..310M , doi : 10.1111/j.1749-6632.1989.tb22465.x , MR 1018637 , S2CID 86300941 。
- ^ Pugh, Anthony (1976), Polyhedra: A Visual Approach , University of California Press, ISBN 978-0-520-03056-5。
- ^ローブ、アーサー・リー(1991年)、空間構造—その調和と対位法(第5版)、ビルクハウザー、ISBN 978-3-7643-3588-5。
- ^ Weisstein, Eric W.「整流化」。MathWorld 。
- ^ハラリー(1972)、82ページ。
- ^ Ryjáček & Vrána (2011) .
- ^ハラリー&ノーマン(1960)。
- ^張と林 (1987)。
- ^エヴァンス&ランビオット(2009年)。
- ^エヴァンス&ランビオット(2010年)。
- ^ Meshulam, Roy (2001-01-01). 「クリーク複合体とハイパーグラフマッチング」. Combinatorica . 21 (1): 89– 94. doi : 10.1007/s004930170006 . ISSN 1439-6912 . S2CID 207006642 .
参考文献
- Beineke, LW (1968)、「Derived charts of digraphs」、Sachs, H.;ヴォス、H.-J.ウォルター、H.-J. (編)、Beiträge zur Graphentheorie 、ライプツィヒ: Teubner、 17–33ページ 。
- ベイネケ, LW (1970)、「導出グラフの特徴づけ」、組合せ理論ジャーナル、9 (2): 129– 135、doi : 10.1016/S0021-9800(70)80019-9、MR 0262097。
- Cvetković, Dragoš; Rowlinson, Peter; Simić, Slobodan (2004), Spectral generalizations of line graphs , London Mathematical Society Lecture Note Series, vol. 314, Cambridge: Cambridge University Press, doi : 10.1017/CBO9780511751752 , ISBN 0-521-83663-8、MR 2120511。
- デジョルジ, ダニエレ・ジョルジオ; サイモン, クラウス (1995)、「線グラフ認識のための動的アルゴリズム」、グラフ理論概念のコンピュータサイエンス (アーヘン, 1995)、コンピュータサイエンス講義ノート、第1017巻、ベルリン: シュプリンガー、pp. 37– 48、doi : 10.1007/3-540-60618-1_64、ISBN 978-3-540-60618-5、MR 1400011。
- エヴァンス, TS; ランビオッテ, R. (2009)、「線グラフ、リンクパーティション、重複コミュニティ」、Physical Review E、80 (1) 016105、arXiv : 0903.2181、Bibcode : 2009PhRvE..80a6105E、doi : 10.1103/PhysRevE.80.016105、PMID 19658772。
- エヴァンス, TS; ランビオッテ, R. (2010)、「重複コミュニティの重み付きネットワークの線グラフ」、ヨーロッパ物理ジャーナルB、77 (2): 265– 272、arXiv : 0912.4389、Bibcode : 2010EPJB...77..265E、doi : 10.1140/epjb/e2010-00261-8、S2CID 119504507。
- グリーンウェル, DL; ヘミンガー, ロバート L. (1972)、「平面線グラフの禁制部分グラフ」、離散数学、2 : 31– 34、doi : 10.1016/0012-365X(72)90058-1、MR 0297604。
- ハラリー、F. ; Norman、RZ (1960)、「線ダイグラフのいくつかのプロパティ」、Rendiconti del Circolo Matematico di Palermo、9 (2): 161–169、doi : 10.1007/BF02854581、hdl : 10338.dmlcz/128114、S2CID 122473974。
- Harary, F. (1972)、「8. 線グラフ」、グラフ理論(PDF)、マサチューセッツ州: Addison-Wesley、pp. 71– 83、2017年2月7日にオリジナル(PDF)からアーカイブ、 2013年11月8日取得。
- Hemminger, RL; Beineke, LW (1978)、「線グラフと線有向グラフ」、Beineke, LW; Wilson, RJ (編)、『グラフ理論の選集』、Academic Press Inc.、pp. 271– 305。
- Jung、HA (1966)、「Zu einem Isomorphiesatz von H. Whitney für Graphen」、Mathematische Annalen (ドイツ語)、164 (3): 270–271、doi : 10.1007/BF01360250、MR 0197353、S2CID 119898359。
- Krausz, J. (1943)、「ホイットニーの新理論のデモ」、Mat.フィズ。ラポック、50 : 75–85、MR 0018403。
- Lehot, Philippe GH (1974)、「線グラフを検出し、そのルートグラフを出力するための最適アルゴリズム」、Journal of the ACM、21 (4): 569– 575、doi : 10.1145/321850.321853、MR 0347690、S2CID 15036484。
- マフレー、フレデリック(1992)「完全線グラフの核」、組合せ理論ジャーナル、シリーズB、55(1):1-8、doi:10.1016/0095-8956(92)90028-V、MR 1159851。
- Metelsky, Yury; Tyshkevich, Regina (1997)、「線形3-ユニフォームハイパーグラフの線グラフについて」、Journal of Graph Theory、25 (4): 243– 251、doi : 10.1002/(SICI)1097-0118(199708)25:4<243::AID-JGT1>3.0.CO;2-K。
- Ramezanpour, A.; Karimipour, V.; Mashaghi, A. (2003)、「無相関ネットワークから相関ネットワークを生成する」、Phys. Rev. E、67 (4) 046107、arXiv : cond-mat/0212469、Bibcode : 2003PhRvE..67d6107R、doi : 10.1103/physreve.67.046107、PMID 12786436、S2CID 33054818。
- ヴァン・ローイ、ACM。Wilf, HS (1965)、「有限グラフの交換グラフ」、Acta Mathematica Hungarica、16 ( 3–4 ): 263–269、doi : 10.1007/BF01904834、hdl : 10338.dmlcz/140421、S2CID 122866512。
- Roussopoulos, ND (1973)、「線グラフGからグラフHを決定するためのmax{ m , n }アルゴリズム」、Information Processing Letters、2 (4): 108–112、doi : 10.1016/0020-0190(73)90029-X、MR0424435 。
- リャチェク、ズデニェク; Vrána、Petr (2011)、「マルチグラフの折れ線グラフと爪のないグラフのハミルトン接続性」、グラフ理論ジャーナル、66 (2): 152–173、doi : 10.1002/jgt.20498、MR 2778727、S2CID 8880045。
- Sedláček, J. (1964), 「交換グラフのいくつかの性質」,グラフ理論とその応用 (Proc. Sympos. Smolenice, 1963) , Publ. House Czechoslovak Acad. Sci., Prague, pp. 145– 150, MR 0173255。
- Sysło, Maciej M. (1982)、「線分有向グラフを認識し、そのルートグラフを出力するラベル付けアルゴリズム」、Information Processing Letters、15 (1): 28– 30、doi : 10.1016/0020-0190(82)90080-1、MR 0678028。
- Trotter, LE Jr. (1977)、「Line perfect graphs」、Mathematical Programming、12 (2): 255– 259、doi : 10.1007/BF01593791、MR 0457293、S2CID 38906333。
- de Werra, D. (1978)、「オンライン完全グラフ」、数学プログラミング、15 (2): 236– 238、doi : 10.1007/BF01609025、MR 0509968、S2CID 37062237。
- ホイットニー, H. (1932)、「合同グラフとグラフの連結性」、アメリカ数学誌、54 (1): 150– 168、doi : 10.2307/2371086、hdl : 10338.dmlcz/101067、JSTOR 2371086。
- 張、富吉。 Lin、Guo Ning (1987)、「On the de Bruijn–Good charts」、Acta Math。シニカ、30 (2): 195–205、MR 0891925。
- Зверович、И。 Э。 (1997)、 Аналог теоремы Уитни для реберных графов мультиграфов и реберные мультиграфы、Diskretnaya Matematika (ロシア語)、9 (2): 98–105、doi : 10.4213/dm478、MR 1468075英語にZverovich, I. È. (1997)「多重グラフのエッジグラフとエッジ多重グラフに対するホイットニー定理の類似」として翻訳されている。離散数学と応用、7 (3): 287– 294、doi : 10.1515/dma.1997.7.3.287、S2CID 120525090 。
外部リンク
- 折れ線グラフ、グラフクラスの包含に関する情報システム
- Weisstein, Eric W. 「折れ線グラフ」。MathWorld 。