ルークのグラフ

ルークのグラフ
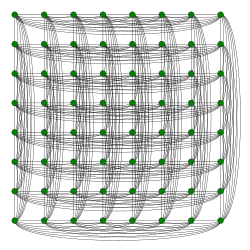8x8 ルークのグラフ
頂点	${\displaystyle nm}$
エッジ	${\displaystyle {\frac {nm(n+m)}{2}}-nm}$
直径	${\displaystyle 2}$
胴回り	${\displaystyle 3}$ （もし）${\displaystyle \max(n,m)\geq 3}$
彩色数	${\displaystyle \max(n,m)}$
スペクトラム	${\displaystyle \{m+n-2,~m-2,~n-2,-2\}}$
プロパティ	積分 完璧 通常 頂点推移 よく覆われた
グラフとパラメータの表

グラフ理論では、ルークのグラフは、チェス盤上のルークの駒のすべての正当な動きを表す無向グラフです。 ルークのグラフの各頂点はチェス盤のマス目を表し、行 (ランク) または列 (ファイル) を共有する 2 つのマス目 (ルークが移動できるマス目) の間には辺が存在します。 これらのグラフは、任意の長方形のチェス盤で作成できます。 ルークのグラフはチェスの伝説ではそれほど重要ではありませんが、グラフの抽象数学では、代替構築を通じてより重要です。 ルークのグラフは、 2 つの完全グラフの直積であり、完全二部グラフの線グラフです。 正方形のルークのグラフは、2 次元のハミンググラフを構成します。

ルークのグラフは対称性が高く、すべての頂点が他のすべての頂点に向かう対称性を持っています。正方形のチェス盤から定義されたルークのグラフでは、より強く、2 つの辺がすべて対称であり、すべての頂点のペアが、同じ移動距離にある他のすべてのペアと対称です (グラフは距離推移的になります)。幅と高さが互いに素である長方形のチェス盤の場合、ルークのグラフは循環グラフになります。1 つの例外を除いて、ルークのグラフは、各辺が属する三角形の数と、隣接していない各頂点のペアを接続する 一意の4閉路の存在という 2 つの特性のみを使用して、他のすべてのグラフと区別できます。

ルークのグラフはパーフェクト グラフです。言い換えると、チェス盤のマス目のすべてのサブセットは、任意の 1 つの行または列に含まれるサブセットのマス目の最大数 (誘導サブグラフのクリーク数)に等しい色数を使用して、1 つの行または列で 2 つのマス目が同じ色にならないように色付けできます。このクラスの誘導サブグラフは、すべてのパーフェクト グラフの特徴となる強いパーフェクト グラフ定理を証明するために使用されるパーフェクト グラフの分解の重要な構成要素です。ルークのグラフの独立数と支配数は、どちらもチェス盤の幅と高さの小さい方に等しくなります。チェスで言えば、独立数とは、互いに攻撃することなく配置できるルークの最大数です。支配数は、ボード上の占有されていないマス目すべてを攻撃するために必要な最小数です。ルークのグラフは十分にカバーされたグラフです。つまり、攻撃していないルークを 1 つずつ配置すると、最大サイズのセットに達するまで行き詰まることはありません。

定義と数学的構成

n × mのルークのグラフは、n × mのチェス盤上のルークの動きを表します。^{[ 1 ]} 頂点はチェス盤のマス目を表し、座標( x , y ) （ 1 ≤ x ≤ n かつ 1 ≤ y ≤ m ）が与えられます。座標( x 1 , y 1 ) と ( x 2 , y 2 ) の 2 つの頂点は、x 1 = x 2またはy ₁ = y ₂の場合にのみ_隣接します_。（x ₁ = x ₂の場合_、頂点は_同じファイルを共有_し、垂直_方向のルークの動きによって接続されます。y ₁ = y ₂の場合、頂点は同じランクを共有し、水平方向のルークの動きによって接続されます。）^{[ 1 ]}

単一の列またはファイルのマス目はすべて互いに直接接続されているため、各列とファイルはクリーク、つまり完全なグラフを形成する頂点のサブセットを形成します。 n × mのチェス盤のルークのグラフ全体は、グラフK _n ◻ K _mの直積として、これらの 2 種類のクリークから形成できます。^{[ 2 ]}正方形のチェス盤のルークのグラフは同じサイズのクリークの直積であるため、ハミンググラフの例です。ハミンググラフとしてのその次元は 2 であり、すべての 2 次元ハミンググラフは正方形のチェス盤のルークのグラフです。^{[ 3 ]}正方形のルークのグラフは「ラテン方陣グラフ」とも呼ばれ、ラテン方陣に適用されると、その辺は同じ値を含むことができないマス目のペアを表します。^{[ 4 ]}数独グラフは、ルークのグラフにいくつかの追加の辺を加えたもので、数独パズルの等しくない値を持つマス目を接続します。^{[ 5 ]}

3-3デュオプリズムは、 3×3のルークグラフを骨格とする4次元凸多面体である。

幾何学的には、ルークのグラフは、隣接する多面体のペアの直積である凸多面体の族の頂点と辺（スケルトン）の集合によって形成されます。^{[ 6 ]}例えば、3-3デュオプリズムは、2つの三角形の直積として形成される4次元形状であり、3×3のルークのグラフをスケルトンとして持っています。^{[ 7 ]}

規則性と対称性

強い規則性

ムーン（1963）とホフマン（1964）は、ルークのグラフ（または、彼らが説明するように、完全な二部グラフの線グラフ）には、次のすべての特性がある ことを指摘しています。${\displaystyle m\times n}$ ${\displaystyle K_{m,n}}$

• チェス盤の各マス目には頂点が1つずつあります。各頂点は辺に隣接しており、同じ段のマス目や同じ列のマス目と繋がっています。${\displaystyle mn}$ ${\displaystyle m\times n}$ ${\displaystyle m+n-2}$ ${\displaystyle m-1}$ ${\displaystyle n-1}$
• ルークのグラフ内の三角形は、同じ段または列にある3つの正方形によって形成されます。 のとき、ちょうど 個の辺（同じ段にある正方形を結ぶ辺）が三角形に属し、残りの 個の辺（同じ列にある正方形を結ぶ辺）が三角形に属します。 のとき、すべての辺が三角形に属します。${\displaystyle m\neq n}$ ${\displaystyle n{\tbinom {m}{2}}}$ ${\displaystyle m-2}$ ${\displaystyle m{\tbinom {n}{2}}}$ ${\displaystyle n-2}$ ${\displaystyle m=n}$ ${\displaystyle m-2=n-2}$
• 隣接しない 2 つの頂点はすべて、一意の-頂点サイクル、つまり 2 つの頂点を角として使用する唯一の長方形に属します。${\displaystyle 4}$

彼らは、 の場合を除いて、これらの性質がルークグラフを一意に特徴づけることを示しています。つまり、ルークグラフは、これらの頂点数、辺数、辺あたりの三角形数を持ち、隣接していない2つの頂点を通る4閉路を一意に持つ唯一のグラフです。^{[ 8 ] [ 9 ]}${\displaystyle m=n=4}$

のとき、これらの条件は、ルークグラフがパラメータ を持つ 強正則グラフであると述べることで簡略化される。これらのパラメータは、それぞれ頂点の数、頂点あたりの辺の数、辺あたりの三角形の数、および隣接しない2つの頂点の共有近傍の数を表す。^{[ 1 ]}逆に、これらのパラメータを持つすべての強正則グラフは、でない限り、ルークグラフでなければならない。^{[ 8 ] [ 9 ]}${\displaystyle m=n}$ ${\displaystyle n\times n}$ ${\displaystyle \operatorname {srg} (n^{2},2n-2,n-2,2)}$ ${\displaystyle n\times n}$ ${\displaystyle n=4}$

トーラス上に埋め込まれたシュリカンデグラフ。これはルークグラフではありませんが、ルークグラフと同じパラメータを持つ強正則グラフです。${\displaystyle 4\times 4}$

のとき、ルークのグラフと同じパラメータを持つ、もう 1 つの強く正則なグラフ、シュリカンデ グラフが存在する。 ^{[ 10 ]} シュリカンデ グラフは、Moon と Moser によって列挙されたのと同じ特性に従う。シュリカンデ グラフは、各頂点の近傍が-サイクルを形成するように接続されている点で、ルークのグラフと区別できる。対照的に、ルークのグラフでは、各頂点の近傍が 2 つの三角形を形成し、1 つはそのランク用、もう 1 つはそのファイル用であり、近傍の 1 つの部分から他の部分への辺はない。^{[ 11 ]}ルークのグラフとシュリカンデ グラフを区別する別の方法は、クリーク カバー数を使用する。ルークのグラフは 4 つのクリーク (チェス盤の 4 つのランクまたは 4 つのファイル) でカバーできるが、シュリカンデ グラフをカバーするには 6 つのクリークが必要である。^{[ 10 ]}${\displaystyle n=4}$ ${\displaystyle 4\times 4}$ ${\displaystyle 4\times 4}$ ${\displaystyle 6}$ ${\displaystyle 4\times 4}$ ${\displaystyle 4\times 4}$ ${\displaystyle n=4}$

対称

ルークのグラフは頂点推移的であり、つまり、すべての頂点から他のすべての頂点に向かう対称性を持つ。これは、すべての頂点に同数の辺があるということを意味する。つまり、それらは-正則 である。ルークのグラフは、標準的なチェスの駒の動きからこのように形成される唯一の正則グラフである。^{[ 12 ]}のとき、ルークのグラフの対称性はグラフの行と列を独立に並べ替えることによって形成されるため、グラフの自己同型群は要素を持つ。 のとき、グラフには行と列を交換する追加の対称性があるため、自己同型の数は である。^{[ 13 ]}${\displaystyle (m+n-2)}$ ${\displaystyle m\neq n}$ ${\displaystyle m!n!}$ ${\displaystyle m=n}$ ${\displaystyle 2n!^{2}}$

ルークのグラフ上の任意の2つの頂点は、隣接しているか隣接していないかに応じて、互いに1または2の距離にあります。任意の2つの隣接していない頂点は、グラフの対称性によって他の任意の2つの隣接していない頂点に変換できます。ルークのグラフが正方形でない場合、隣接する頂点のペアは、水平方向に隣接しているか垂直方向に隣接しているかに応じて対称群の2つの軌道に収まりますが、グラフが正方形の場合、任意の2つの隣接する頂点は対称性によって互いにマッピングされるため、グラフは距離推移的です。^{[ 14 ]}

とが互いに素であるとき、ルークグラフの対称群は、頂点を巡回的に入れ替える作用を持つ巡回群を部分群として含む。したがって、この場合、ルークグラフは巡回グラフである。^{[ 15 ]}${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle S_{m}\times S_{n}}$ ${\displaystyle C_{mn}=C_{m}\times C_{n}}$ ${\displaystyle mn}$

スクエアルークのグラフは連結同質的であり、2つの連結された誘導サブグラフ間の同型性はすべてグラフ全体の自己同型に拡張できることを意味する。^{[ 16 ]}

その他の特性

完璧

3×3のルークグラフ（ 3-3デュオプリズムのグラフ）は、3色で彩色され、3つの頂点からなるクリークを示しています。このグラフとその誘導部分グラフの彩色数はクリーク数と等しいため、パーフェクトグラフとなります。

ルークのグラフは、完全二部グラフK _{n , m}の線グラフとして見ることもできます。つまり、K _{n , m}の各辺に対して 1 つの頂点があり、ルークのグラフの 2 つの頂点が隣接するのは、完全二部グラフの対応する辺が共通の端点を共有している場合のみです。^{[ 2 ] [ 17 ]}この見方では、完全二部グラフの一方の側のi番目の頂点からもう一方の側のj番目の頂点への辺は、座標( i , j )のチェス盤のマス目に対応します。^{[ 1 ]}

任意の二部グラフは完全二部グラフのサブグラフであり、同様に、任意の二部グラフの線グラフはルークグラフの誘導サブグラフである。 ^{[ 18 ]}二部グラフの線グラフは完全である。すなわち、二部グラフの線グラフとその誘導サブグラフの頂点彩色に必要な色の数は、最大の完全サブグラフの頂点数と同じである。二部グラフの線グラフは、完全グラフの重要なファミリーを形成し、Chudnovsky ら (2006)が完全グラフを特徴付け、奇数ホールと奇数アンチホールのないグラフはすべて完全であることを示すために使用した少数のファミリーの 1 つである。^{[ 19 ]}特に、ルークグラフ自体は完全である。

有限群のケーリー表から得られるチェス盤グラフの8色塗り

ルークのグラフはパーフェクトなので、グラフを彩色する際に必要な色の数は、その最大のクリークのサイズだけです。ルークのグラフのクリークは、単一の行または単一の列のサブセットであり、これらの最大のものはサイズがmax( m、n )であるため、グラフの彩色数でもあります。n × nルークのグラフのn彩色は、ラテン方陣として解釈できます。つまり、 n × nグリッドの行と列をn個の異なる値で埋める方法を記述し、どの行または列にも同じ値が2回出現しないようにします。^{[ 20 ]}同様に、長方形のルークのグラフの彩色は、ラテン長方形に対応します。^{[ 21 ]}ルークのグラフの最適な彩色を見つけることは簡単ですが、部分彩色をグラフ全体の彩色に拡張できるかどうかを判断することはNP 完全です(この問題は、事前彩色拡張と呼ばれます)。同様に、部分ラテン方陣が完全なラテン方陣に完成できるかどうかを判断することもNP完全である。^{[ 22 ]}

独立

	1つの	b	c	d	e	f	グラム	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	1つの	b	c	d	e	f	グラム	h

チェス盤上に8つのルークを攻撃せずに配置し、対応するルークのグラフで最大の独立集合を形成する

ルークのグラフにおける独立集合とは、グラフの同じ行または列に属さない頂点の集合である。チェスの用語で言えば、互いに攻撃し合うことのないルークの配置に相当する。完全グラフとは、すべての誘導サブグラフにおいて、最大の独立集合の大きさが、グラフの頂点を最小数のクリークに分割したときのクリークの数に等しいグラフとも言える。ルークのグラフでは、行の集合または列の集合（集合数が少ない方）がこのような最適な分割を形成する。したがって、グラフにおける最大の独立集合の大きさはmin( m , n )となる。^{[ 1 ]}

ルークのグラフは十分に被覆されたグラフである。ルークのグラフ内のすべての独立集合は最大独立集合まで拡張でき、ルークのグラフ内のすべての最大独立集合は同じサイズmin( m , n )を持つ。^{[ 23 ]}

支配

グラフの支配数とは、すべての支配集合の中で最小の基数である。ルークのグラフにおいて、頂点の集合が支配集合となるのは、対応するマス目がm×nの盤上のすべてのマス目を占めるか、またはルークの手数ですべてのマス目から遠ざかる場合のみである。m × nの盤面では、支配数はmin( m , n )である。^{[ 24 ]}

ルークのグラフにおいて、k支配集合とは、対応するマス目が（ルークの動きによって）他のすべてのマス目を少なくともk回攻撃する頂点の集合である。ルークのグラフにおけるk組支配集合とは、対応するマス目が他のすべてのマス目を少なくともk回攻撃し、かつそれ自体が少なくともk − 1回攻撃される頂点の集合である。すべてのk支配集合およびk組支配集合の中での最小の基数は、それぞれk支配数およびk組支配数である。正方形の盤上で、kが偶数の場合、n ≥ ( k ² − 2 k )/4かつk < 2 nのとき、 k支配数はnk /2である。同様に、kが奇数で2 n未満のとき、 k組支配数はn ( k + 1)/2である。^{[ 25 ]}

ハミルトン性

すべてのルークのグラフにはハミルトンサイクルが含まれる。^{[ 26 ]}しかし、これらのサイクルは、チェス盤の1つの行または列内の遠く離れたマス目間の移動を含む場合がある。チェスの数学における「ルークのツアー」の研究は、一般的に、ルークが隣接するマス目への移動のみに制限される、これらのハミルトンサイクルの特殊なケースに集中してきた。これらのシングルステップのルークのツアーは、偶数個のマス目を持つ盤上でのみ存在する。これは、標準的なチェス盤から反対色の2つのマス目を取り除けば、残りのマス目は常にドミノで覆うことができるというゴモリーの定理の証明において中心的な役割を果たす。 ^{[ 27 ]}チェスの駒のツアーについて論じた最初の著作である、9世紀のサンスクリット語の『ルドラタのカヴィヤランカラ』では、ナイトのツアーと並んで取り上げられている。^{[ 28 ]}

スペクトラム

ルークのグラフのスペクトル（隣接行列の固有値）は、4 つの固有値、、、およびで構成される。これらはすべて整数なので、ルークのグラフは整数グラフである。 4 つの固有値を持ち、その 4 つのうちの 1 つが であるグラフのクラスは 3 つだけ（また、例外的なグラフは有限個存在する）あり、その 3 つのクラスのうちの 1 つがルークのグラフのクラスである。 と のほとんどの組み合わせについて、ルークのグラフはスペクトル的に一意である。つまり、他のグラフが同じスペクトルを持つことはない。特に、または のとき、または と の 2 つの数の合計が18 以上で の形式にならないときに、このことが当てはまる。^{[ 29 ]}${\displaystyle m+n-2}$ ${\displaystyle m-2}$ ${\displaystyle n-2}$ ${\displaystyle -2}$ ${\displaystyle -2}$ ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle m\times n}$ ${\displaystyle n=2}$ ${\displaystyle n=m-1}$ ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle 2t^{2}\pm t}$

他のグラフでは

各頂点の近傍がルークグラフを誘導するグラフは、局所グリッドと呼ばれています。例としては、各頂点の近傍がルークグラフを形成するジョンソングラフ が挙げられます。他にも多くの例が知られており、一部のルークグラフについては完全な分類が知られています。例えば、近傍がすべてルークグラフであるグラフが2つあります。それらはジョンソングラフと、ルークグラフの補グラフです。 ^{[ 30 ]}${\displaystyle J(n,k)}$ ${\displaystyle k\times (n-k)}$ ${\displaystyle 3\times 3}$ ${\displaystyle J(6,3)}$ ${\displaystyle 4\times 4}$

参照

• ビショップグラフ
• チェス盤複合体、ルークのグラフの独立複合体
• キングのグラフ
• ナイトのグラフ
• 格子グラフ、チェス盤上のマス目の水平および垂直の隣接関係を示すグラフ
• クイーンのグラフ

参考文献

1. Laskar, Renu ; Wallis, Charles (1999)、「チェスボードグラフ、関連デザイン、および支配パラメータ」、Journal of Statistical Planning and Inference、76 ( 1– 2): 285– 294、doi : 10.1016/S0378-3758(98)00132-3、MR  1673351。
2. ストーンズ、ダグラス・S.（2010）、「ラテン長方形の数に関する多くの公式」、電子組合せ論ジャーナル、17（1）A1：記事1、46、doi：10.37236 / 487、MR 2661404 
3. Azizoğlu, M. Cemil; Eğecioğlu, Ömer (2003)、「ハミンググラフにおける次元正規化境界を最小化する極値集合」、SIAM Journal on Discrete Mathematics、17 (2): 219– 236、doi : 10.1137/S0895480100375053、MR 2032290 。
4. Goethals, J.-M.; Seidel, JJ (1970)、「組み合わせ設計から導かれる強く正則なグラフ」、Canadian Journal of Mathematics、22 (3): 597– 614、doi : 10.4153/CJM-1970-067-9、MR 0282872、S2CID 199082328  。
5. Herzberg, Agnes M. ; Murty, M. Ram (2007)、「数独の正方形と彩色多項式」(PDF)、アメリカ数学会誌、54 (6): 708– 717、MR 2327972 
6. Matschke, Benjamin; Pfeifle, Julian; Pilaud, Vincent (2011)、「Prodsimplicial-neighborly polytopes」、Discrete & Computational Geometry、46 (1): 100– 131、arXiv : 0908.4177、doi : 10.1007/s00454-010-9311-y、MR 2794360、S2CID 2070310  
7. ムーア、ダグ（1992）、「単純体を理解する」、カーク、デイビッド（編）、グラフィックス・ジェムズIII、アカデミック・プレス、pp.  250– 255、doi：10.1016 / b978-0-08-050755-2.50057-9、ISBN 978-0-12-409673-8
8. Moon, JW (1963)、「完全なバイグラフの線グラフについて」、Annals of Mathematical Statistics、34 (2): 664– 667、doi : 10.1214/aoms/1177704179。
9. Hoffman, AJ (1964)、「完全二部グラフの線グラフについて」、Annals of Mathematical Statistics、35 (2): 883– 885、doi : 10.1214/aoms/1177703593、MR 0161328 。
10. Fiala, Nick C.; Haemers, Willem H. (2006)、「5-chromatic stronger regular graphs」、Discrete Mathematics、306 (23): 3083– 3096、doi : 10.1016/j.disc.2004.03.023、MR 2273138 。
11. ブリチェンコ副社長; Makhnev, AA (2011)、「Об автоморфизмах сильно регулярных локально циклических графов」 [強く正則な局所循環グラフの自己同型について]、Doklady Akademii Nauk (inロシア語)、441 (2): 151–155、MR 2953786 . Doklady Mathematics 84 (3): 778–782, 2011, doi : 10.1134/S1064562411070076に翻訳。翻訳の1ページ目より：「シュリカンデグラフは、パラメータ(16, 6, 2, 2)を持つ唯一の強正則な局所六角形グラフである。」
12. Elkies, Noam (2004年秋)、「グラフ理論用語集」、新入生セミナー23j: チェスと数学、ハーバード大学数学部、2023年5月3日閲覧。。
13. ハラリー、フランク（1958）、「二色グラフの数について」、パシフィック・ジャーナル・オブ・マスマティクス、8（4）：743-755、doi：10.2140/pjm.1958.8.743、MR 0103834 ルークのグラフの自己同型群については特に式(10)（p.748）を参照し、この群の位数については式の上の議論を参照。${\displaystyle n\times n}$
14. ビッグス、ノーマン（1974）「線グラフの対称性」、ユーティリタス・マセマティカ、5：113-121、MR 0347684 。
15. これは、ルークのグラフを直積グラフとして定義すること、およびBroere, Izak; Hattingh, Johannes H. (1990)「循環グラフの積」Quaestiones Mathematicae、13 (2): 191– 216、doi : 10.1080/16073606.1990.9631612、MR 1068710の命題4に従う。 。
16. Gray, R.; Macpherson, D. (2010)、「Countable connected-homogeneous graphs」、Journal of Combinatorial Theory、Series B、100 (2): 97– 118、doi : 10.1016/j.jctb.2009.04.002、MR 2595694 特に定理1を参照してください。定理1では、これらのグラフが完全な二部グラフの線グラフであると識別されます。
17. 完全グラフの直積と完全二部グラフの線グラフの同値性については、 de Werra, D.; Hertz, A. (1999) 「グラフの和の完全性について」（PDF） , Discrete Mathematics , 195 ( 1– 3): 93– 101, doi : 10.1016/S0012-365X(98)00168-X , MR 1663807を参照。 。
18. de Werra & Hertz (1999) .
19. マリア・チュドノフスキー、ニール・ロバートソン、ポール・シーモア、ロビン・トーマス(2006)、「強完全グラフ定理」(PDF)、Annals of Mathematics、164 (1): 51– 229、arXiv : math/0212070、doi : 10.4007/annals.2006.164.51、JSTOR 20159988、S2CID 119151552  。
20. 辺彩色完全二部グラフとラテン方陣の同値性については、例えば、 LeSaulnier, Timothy D.; Stocker, Christopher; Wenger, Paul S.; West, Douglas B. (2010) 「Rainbow matching in edge-colored graphs」、Electronic Journal of Combinatorics、17 (1): Note 26, 5、doi : 10.37236/475、MR 2651735を参照。 。
21. ストーンズ、ダグラス・S. (2010)、「ラテン長方形の数に関する多くの公式」、電子ジャーナル・オブ・コンビナトリクス、17 (1) A1: A1:1–A1:46、doi : 10.37236/487、MR 2661404 
22. Colbourn, Charles J. (1984)、「部分ラテン方陣完成の複雑さ」、Discrete Applied Mathematics、8 (1): 25– 30、doi : 10.1016/0166-218X(84)90075-1、MR 0739595 。
23. ルークのグラフのwell-covered propertyと同等の記述として、完全二部グラフのマッチングに関する記述については、 Lesk, M.; Plummer, MD; Pulleyblank, WR (1984)「Equi-matchable graphs」、Bollobás, Béla (ed.), Graph Theory and Combinatorics: Proceedings of the Cambridge Combinatorial Conference, in Honour of Paul Erdős、London: Academic Press、pp.  239– 254、MR 0777180を参照。 。
24. Yaglom, AM ; Yaglom, IM (1987)、「問題34bの解答」、Challenging Mathematical Problems with Elementary Solutions、ドーバー、p. 77、ISBN 9780486318578。
25. Burchett, Paul; Lane, David; Lachniet, Jason ( 2009)「ルークのグラフにおけるK支配とk組支配およびその他の結果」 Congressus Numerantium、199 : 187–204。
26. Hurley, CB; Oldford, RW (2011年2月)、「高次元データ空間におけるナビゲーションインフラストラクチャとしてのグラフ」、Computational Statistics、26 (4): 585– 612、doi : 10.1007/s00180-011-0228-6、S2CID 54220980 
27. ワトキンス、ジョン・J.（2004）、アクロス・ザ・ボード：チェス盤問題の数学、プリンストン大学出版、  p.12、ISBN 9780691130620
28. マレー、HJR（1902年1月）「ナイトの旅：古代と東洋」『ブリティッシュ・チェス・マガジン』第22巻第1号、 1～ 7ページ 
29. ドゥーブ、マイケル（1970）「4つの固有値を持つ特定のグラフをスペクトルで特徴付けることについて」線形代数とその応用、3（4）：461-482、doi：10.1016/0024-3795（70）90037-6、MR 0285432 
30. Cohen, Arjeh M. (1990)、「グラフ、建物、および関連幾何学の局所認識」(PDF)、Kantor, William M.、Liebler, Robert A.、Payne, Stanley E.、Shult, Ernest E. (編)、『有限幾何学、建物、および関連トピックス：1988年7月17～23日にコロラド州ピングリーパークで開催された建物および関連幾何学に関する会議の論文』、Oxford Science Publications、オックスフォード大学出版局、pp.  85～ 94、MR 1072157 特に89～90ページを参照

外部リンク

• ワイスタイン、エリック W.、「ルークグラフ」、MathWorld