天文学における視差

年周視差による恒星の視差運動。頂角の半分が視差角です

青い点（左）は観測者を表しています。異なる位置から星（右）まで直線を引き、2つの点の間の角度（α）を測定することで、天文学者は地球と星の間の距離を測定できます。

天文学において、視差とは、観測者の視点の変化によって引き起こされる、近くの天体の遠くの背景の物体に対する位置の見かけ上の変化です。この効果は、地球の公転周期における2つの異なる位置（通常は6か月離れている）から近くの星までの距離を測定するために最も一般的に使用されます。ある測定点から別の測定点までの星の位置の変化の尺度である視差角を測定することで、天文学者は三角法を使用して星までの距離を計算できます

この概念は、地球の軌道上の2つの異なる点と、もう一方の端にある恒星によって形成される三角形の幾何学に基づいています。視差角は、これら2つの視線間の恒星における角度（α）の半分です。恒星が観測者に近いほど、この角度は大きくなります

視差は、天文学者が宇宙の距離を測定するために使用する一連の技術である宇宙距離ラダーの基本的な方法です。視差は近くの恒星までの距離を測定する場合にのみ有効ですが、ガイアのような宇宙望遠鏡はその有効性を大幅に拡大しました。視差は恒星までの距離を測定するための最も直接的で信頼性の高い方法であり、銀河やそれより遠くまでの距離を測定するためのより間接的な方法を較正するための基礎となっています。

パーセク

パーセクとは、太陽から視差角が1秒角の天体までの距離です（縮尺通りではありません）。

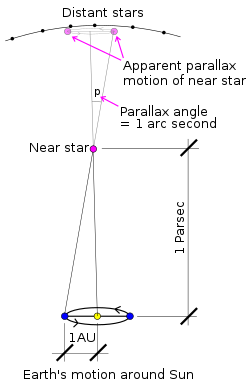
パーセク（記号：pc）は、太陽系外の天体までの遠距離を測定するために使用される長さの単位で、約3.26光年または206,265天文単位（AU）、つまり30.9 兆キロメートル（19.2兆マイル）に相当します。^{[a]パーセクという単位は、}視差と三角法を用いて得られ、1AUが1秒角の角度を占める距離として定義されています^[1]（ 1/3600⁠約 1度）。最も近い恒星であるプロキシマ・ケンタウリは、太陽から約 1.3 パーセク (4.2 光年) 離れています。この距離から、地球と太陽の間隔は 1 秒角をわずかに下回ります。^[2]肉眼で見えるほとんどの恒星は太陽から数百パーセク以内にあり、最も遠い恒星でも数千パーセク、アンドロメダ銀河では 70 万パーセクを超えます。^[3]

パーセクという言葉は、 1秒の視差に対応する距離の短縮形で、1913年にイギ​​リスの天文学者ハーバート・ホール・ターナーによって造られました^。[4]この単位は、生の観測データから天文距離を計算することを簡素化するために導入されました。この理由もあって、天文学や天体物理学ではパーセクが好まれる単位となっていますが、一般科学の教科書や一般的な用法では光年が依然として主流です。パーセクは天の川銀河内の短距離に使用されますが、宇宙のより大きなスケールにはパーセクの倍数が必要です。天の川銀河内および周辺のより遠方の天体にはキロパーセク（kpc）、中距離銀河にはメガパーセク（Mpc）、多くのクエーサーや最も遠方の銀河 にはギガパーセク（Gpc）が必要です

2015年8月、国際天文学連合（IAU）は決議B2を可決しました。この決議は、標準化された絶対等級および見かけの放射等級尺度の定義の一部として、パーセクの既存の明示的な定義を、正確に 648000/πau  、またはおよそ30856775814913673メートルとしました。これは、IAU 2012による天文単位のメートルの正確な定義に基づいています。これは、 多くの天文学の参考文献に記載されているパーセクの小角定義に対応しています。^{[5] [6]}

恒星視差

恒星視差の運動

地球と恒星の相対運動によって生じる恒星視差は、コペルニクスモデルでは、地球が太陽の周りを公転することから生じると見ることができます。つまり、恒星は空のより遠くの物体に対してのみ動いているように見えます。静止モデルでは、恒星の動きは、背景の恒星に対して恒星が空を横切って振動しているという 現実のものとして捉えなければなりません

恒星視差は、ほとんどの場合、年視差を使用して測定されます。年視差は、地球と太陽から見た恒星の位置の差、つまり、地球が太陽を回る軌道の平均半径によって恒星に課される角度として定義されます。パーセク(3.26光年) は、年視差が 1秒角である距離として定義されます 。年視差は通常、地球が軌道上を移動するときの 1年のさまざまな時点での恒星の位置を観測することによって測定されます。年視差の測定は、最も近い恒星までの距離を決定する最初の信頼性の高い方法でした。恒星視差の最初の成功した測定は、1838 年にフリードリヒ ベッセルがヘリオメーターを使用して、はくちょう座 61 番星に対して行いました。^[7]恒星視差は、他の測定方法の較正の基準となっています。恒星の視差に基づく正確な距離計算には、地球から太陽までの距離の測定が必要であり、現在は惑星表面からのレーダー反射に基づいています。 ^[8]

これらの計算に含まれる角度は非常に小さいため、測定が困難です。太陽に最も近い恒星（したがって視差が最も大きい恒星）であるプロキシマ・ケンタウリの視差は0.7687±0.0003秒角です。^[9]この角度は、直径2センチメートルの天体が5.3キロメートル離れた場所に 広がる角度とほぼ同じです。

ハッブル宇宙望遠鏡- 空間スキャンにより、最大1万光年の距離を正確に測定します（2014年4月10日）。^[10]

当時、恒星の視差が小さすぎて観測できなかったという事実は、近世初期において地動説に反する主な科学的論拠として用いられました。ユークリッド幾何学から、恒星が十分に遠ければその効果は検出できないことは明らかですが、様々な理由から、そのような巨大な距離は全くあり得ないと思われました。ティコがコペルニクスの地動説に反論した主な理由の一つは、観測可能な恒星の視差が存在しないという前提と矛盾するためには、土星（当時最も遠い既知の惑星）の軌道と第8球面（恒星）の間に巨大で不可能な空間が存在しなければならないというものでした。 ^[11]

1989年、衛星ヒッパルコスが打ち上げられたのは、主に10万個を超える近傍の恒星の視差と固有運動の測定精度を向上させるためで、この方法の有効範囲は10倍に拡大した。しかし、ヒッパルコスが測定できたのは、天の川銀河の直径の1%強にあたる約1,600光年離れた恒星の視差角のみであった。 2013年12月に打ち上げられた欧州宇宙機関のガイア・ミッションでは、視差角を10マイクロ秒角の精度で測定できるため、地球から数万光年離れた近傍の恒星（および惑星の可能性もある）の地図を作成できる。^{[12] [13]} 2014年4月、NASAの天文学者たちは、ハッブル宇宙望遠鏡が空間スキャンを使用することで、最大1万光年離れた距離を正確に測定できると報告した。これは、以前の測定に比べて10倍の改善である。^[10]

日周視差

日周視差は、地球の自転や地球上の位置の違いによって変化する視差です。地球上の異なる観測位置（ある瞬間）から見た月、そしてある程度は地球型惑星や小惑星は、恒星を背景にして異なって見えることがあります。 ^{[14] [15]}

日周視差は、1672年にジョン・フラムスティードによって火星の衝における距離を測定するために使用され、それを通して天文単位と太陽系の大きさを推定しました。^[16]

月の視差

月視差（多くの場合、月水平視差または月赤道水平視差の略）は、（日周）視差の特殊なケースです。最も近い天体である月は、あらゆる天体の中で最も大きな最大視差を持ち、時には1度を超えます。^[17]

恒星視差の図は、図を縮小して少し修正すれば、月の視差も表すことができます。「近くの星」を「月」と読み替え、図の下部にある円を太陽の周りの地球の公転軌道の大きさを表すものとしてではなく、地球の球体の大きさと地球表面の周りの円と見なしてください。そうすると、月の（水平）視差は、地球上の2つの異なる観測位置から見た、遠くの星の背景に対する月の角度位置の差に相当します。

観測位置の1つは、特定の瞬間に月が真上に見える場所です。つまり、図の垂直線に沿って見た場合です。もう1つの観測位置は、同じ瞬間に月が地平線上にある場所です。つまり、修正された図の青い点の1つにほぼ対応する地球表面の位置から、対角線の1つに沿って見た場合です

月の（水平）視差は、月までの距離を地球の半径で割った角度として定義することもできます^{[18] [19]}。これは、上記のように縮小および修正された図の角度pに等しくなります

月の水平視差は、いつでも地球から月までの直線距離によって決まります。地球と月の間の直線距離は、月が地球の周りを摂動を受けながらほぼ楕円軌道を描くにつれて、連続的に変化します。直線距離の変化範囲は地球半径の約56倍から63.7倍で、水平視差は約1度ですが、約61.4分から約54分の範囲です。^[17]天文年鑑や同様の出版物は、天文学者（および天文航海士）の便宜のために、月の水平視差や地球から月までの直線距離を定期的に（例えば毎日）表にまとめており、この座標が時間とともにどのように変化するかを研究することは、月の理論の一部を形成しています。

月の毎日の視差の図

視差は月までの距離を 決定するためにも使用できます

ある場所から月の視差を決定する方法の1つは、月食を利用することです。地球の完全な影が月に落ちる場合、その見かけの曲率半径は、月から見た地球と太陽の見かけの半径の差に等しくなります。この半径は0.75度と見られ、そこから（太陽の見かけの半径0.25度と合わせて）地球の見かけの半径は1度となります。これにより、地球と月の距離は地球半径の60.27倍、つまり384,399キロメートル（238,854マイル）となります。この手順は、サモス島のアリスタルコス^[20]とヒッパルコスによって初めて使用され、後にプトレマイオス[ ^21]の著作にも取り入れられました

右の図は、地球が惑星系の中心にあり、自転しない地心説と地静説の惑星モデルにおいて、月の日周視差がどのように生じるかを示しています。また、視差は観測者の動きによって引き起こされる必要はなく、観測対象の動きのみから生じる可能性があるという重要な点も示しています。これは、視差の定義によっては、視差は観測者の動きによって引き起こされるという説明とは異なります。

別の方法は、地球上の2つの場所から同時に月の写真を2枚撮影し、星に対する月の位置を比較することです。地球の向き、これらの2つの位置測定値、そして地球上の2つの場所間の距離を用いて、月までの距離を三角測量することができます。

${\displaystyle \mathrm {distance} _{\mathrm {moon} }={\frac {\mathrm {distance} _{\mathrm {observerbase} }}{\tan(\mathrm {angle} )}}}$

月視差の例：月によるプレアデス星団の掩蔽

これは、ジュール・ヴェルヌが1865年の小説『月世界旅行』で 言及した方法です

それまで、多くの人々は月と地球の距離をどのように計算できるのか全く知りませんでした。この状況を利用して、この距離は月の視差を測定することで得られると教えられました。視差という言葉に驚いた人には、地球の半径の両端から月まで伸びる2本の直線のなす角度だと説明されました。この方法の完璧さに疑問を抱いた人には、この平均距離が23万4347マイル（94,330リーグ）になるだけでなく、天文学者の誤差は70マイル（≈30リーグ）以下であることがすぐに示されました。

太陽視差

コペルニクスが地球が太陽の周りを公転する太陽中心説を提唱した後、スケールのない太陽系全体のモデルを構築することが可能になりました。スケールを確定するには、太陽系内の1つの距離、例えば地球から太陽までの平均距離（現在は天文単位、AUと呼ばれています）を測定するだけで済みます。三角測量によって求められた場合、これは太陽視差と呼ばれ、地球の中心から見た太陽の位置と地球半径1つ離れた点から見た太陽の位置の差、つまり地球の平均半径が太陽に対して張る角度です。太陽視差と地球の平均半径がわかれば、AUを計算することができます。これは、可視宇宙の 大きさと膨張年齢^{[22]を確定するための長い道のりの最初の小さな一歩です}

太陽までの距離を月までの距離で測る原始的な方法は、サモス島のアリスタルコスが著書『太陽と月の大きさと距離について』の中で既に提案していた。彼は、上弦または下弦の月が満ち欠けする瞬間に、太陽、月、地球が直角三角形（月が直角）を形成することに注目した。そして、月・地球・太陽の角度を87度と推定した。正確な幾何学を用いながらも不正確な観測データに基づき、アリスタルコスは太陽が月よりも20倍弱遠いと結論付けた。この角度の真の値は89度50分に近く、太陽は約390倍遠い。^[20]

アリスタルコスは、月と太陽の見かけの角度の大きさはほぼ同じであり、したがって、それらの直径は地球からの距離に比例するはずだと指摘しました。したがって、彼は太陽は月の約20倍の大きさであると結論付けました。この結論は誤りではありますが、彼の誤ったデータから論理的に導かれています。これは太陽が地球よりも大きいことを示唆しており、太陽中心説を支持するものと解釈できます。^[23]

金星の太陽面通過時間を測定し、太陽視差を決定する

アリスタルコスの推定結果は観測誤差のために不正確でしたが、視差の正しい幾何学的原理に基づいており、1761年と1769年に金星の太陽面通過が正しく観測されるまで、ほぼ2000年間、太陽系の大きさの推定の基礎となりました。 ^{[20]この方法は1716年に}エドモンド・ハレーによって提案されましたが、彼はその結果を見ることはありませんでした。金星の太陽面通過の利用はブラックドロップ効果のために期待されたほど成功しませんでしたが、結果として得られた推定値1億5300万キロメートルは、現在受け入れられている値1億4960万キロメートルをわずか2%上回るものです

ずっと後になって、太陽系は小惑星の視差を用いて「スケール化」されました。エロスのように、金星よりも地球にずっと近い位置を通過する小惑星もあります。好ましい衝では、エロスは地球に2200万キロメートル以内に近づくことができます。^[24] 1900年から1901年の衝の間、エロスの視差を測定して太陽視差^[25]（または太陽までの距離）を決定する世界的なプログラムが開始され、その結果は1910年にケンブリッジのアーサー・ヒンクス^[26]とカリフォルニア大学リック天文台のチャールズ・D・ペリン^[27]によって発表されました

^{ペリーヌは1906年[28]}と1908年に進捗報告書を発表しました^[29]。彼はクロスリー反射望遠鏡で965枚の写真を撮影し、そのうち525枚を測定用に選びました^{[30] 。その後、1930年から1931年にかけて、}ハロルド・スペンサー・ジョーンズによって、より接近した際に同様のプログラムが実施されました^[31]。このプログラムによって得られた天文単位（おおよそ地球と太陽の間の距離）の値は、レーダーと動的視差法によってより正確な測定値が得られるようになった 1968年まで、決定的なものと考えられていました

また、金星（1958年）とイカロスのような小惑星の両方からのレーダー反射は、太陽視差の決定に使用されてきました。今日では、宇宙船のテレメトリリンクの使用により、この古い問題は解決されました。現在受け入れられている太陽視差の値は 8.794 143秒角です。^[32]

移動星団視差

おうし座の散開星団ヒアデスは、空の20度という非常に広い範囲に広がっているため、天文測定から得られる固有運動は、オリオン座の北の透視点にある程度正確に収束するように見えます。観測された見かけの（角）固有運動（秒角）と、恒星スペクトル線のドップラー赤方偏移によって観測される、同じく観測された真の（絶対）後退運動を組み合わせることで、年視差を使用するのとほぼ同じ方法で、星団（151光年）とその構成星までの距離を推定できます。^[33]

動的視差

力学的視差は、爆発の光学波面が周囲の塵の雲を見かけの角速度で伝播しているのが見られる場合、超新星までの距離を決定するために使用されることもあります。ただし、その真の伝播速度は光速であることが知られています。^[34]

時空間視差

拡張相対論的測位システムから、通常の視差の概念を空間のみで一般化する時空間視差が開発されました。これにより、例えばPPN形式で使用されるような質量の大きい物体による光の屈曲の中間モデルなしに、時空における事象場を直接推定することができます。 ^[35]

統計的視差

2つの関連する手法は、星の運動をモデル化することで星の平均距離を決定できます。どちらも統計視差と呼ばれ、個別には永年視差と古典的統計視差と呼ばれます

太陽の宇宙空間における運動は、視差測定の精度を向上させる長い基線（セキュラー・パララックス）をもたらす。天の川銀河内の恒星の場合、これは平均基線4 AU/年に相当する。ハロー星の場合、基線は40 AU/年である。数十年後には、この基線は従来の視差測定に用いられる地球・太陽間の基線よりも桁違いに大きくなる可能性がある。セキュラー・パララックスでは、他の恒星との相対速度が未知数となるため、不確実性のレベルは高くなる。複数の恒星のサンプルに適用することで、不確実性を低減できる。精度はサンプルサイズの平方根に反比例する。 ^[36]

多数の星の平均視差と距離は、それらの視線速度と固有運動から推定できます。これは古典的な統計視差として知られています。星の運動は、距離に基づいて速度分散を統計的に再現するようにモデル化されます。^{[36] [37]}

天文学におけるその他の距離測定方法

天文学において、「視差」という用語は、必ずしも真の視差を利用しない距離の推定方法を意味するようになりました。例えば、

• 測光視差法
• 分光視差
• 動的視差

参照

• 宇宙距離ラダー
• 月までの距離（天文学）

注記

1. ここでの1兆は短尺、つまり10の12^乗（長尺では10億、10億）です。

参考文献

1. 「宇宙距離スケール - 天の川」。2014年9月24日閲覧
2. ベネディクト、G. F.、他「精密誘導センサー#3の天体測定安定性と精度：プロキシマ・ケンタウリの視差と固有運動」（PDF）。HSTキャリブレーション・ワークショップの議事録。380  ～ 384ページ。 2007年7月11日閲覧。
3. 「最も遠い星々」。StarDate 。テキサス大学オースティン校。2021年5月15日。2021年9月5日閲覧
4. ダイソン、F. W. (1913年3月). 「キャリントン周極カタログにおける星の空間分布」.王立天文学会月報. 73 (5): 342.書誌コード: 1913MNRAS..73..334D. doi : 10.1093/mnras/73.5.334 . [段落14、342ページ] 距離の単位R*を1秒の視差に対応するものとし、[…脚注:] * この距離の単位には名称が必要です。シャルリエ氏はシリオメーターを提案しましたが、ギリシャ語への悪影響を無視できるのであれば、アストロンという言葉を採用してもよいでしょう。ターナー教授はパーセクを提案しており、これは「1秒の視差に対応する距離」の略語と解釈できます
   
5. コックス、アーサー・N.編 (2000).アレンの天体物理学的量（第4版）. ニューヨーク: AIP Press / Springer.書誌コード:2000asqu.book.....C. ISBN 978-0387987460。
6. ビニー、ジェームズ；トレメイン、スコット (2008).銀河ダイナミクス（第2版）. プリンストン、ニュージャージー：プリンストン大学出版局.書誌コード:2008gady.book.....B. ISBN 978-0-691-13026-2。
7. ザイリク＆グレゴリー 1998, p. 44.
8. ザイリク＆グレゴリー 1998, § 22-3
9. ベネディクト、G. フリッツ他 (1999). 「ハッブル宇宙望遠鏡精密誘導センサー3を用いたプロキシマ・ケンタウリとバーナード星の干渉天体測定：恒星下伴星の検出限界」天文学ジャーナル. 118 (2): 1086–1100 . arXiv : Astro-ph/9905318 .書誌コード:1999AJ....118.1086B. doi :10.1086/300975. S2CID  18099356
10. ハリントン、JD、ヴィラード、レイ（2014年4月10日）「NASA​​のハッブル宇宙望遠鏡、恒星の巻き尺を宇宙に10倍延長」NASA。2014年4月12日時点のオリジナルからアーカイブ。 2014年4月11日閲覧。
11. ドブジツキ、J.（1973年）。ドブジツキ、イェルジ（編）。コペルニクスの太陽中心説の受容。51ページ。doi : 10.1007/978-94-015-7614-7。ISBN  978-90-481-8340-1。
12. 「ソユーズST-B、ガイア宇宙観測衛星の打ち上げに成功」nasaspaceflight.com. 2013年12月19日。2013年12月19日時点のオリジナルよりアーカイブ。 2013年12月19日閲覧。
13. ポール・J・ヘニー「ESAのガイア宇宙観測ミッション」Astronomy Today。2008年3月17日時点のオリジナルよりアーカイブ。 2008年3月8日閲覧。
14. 資料。University Science Books。123～125ページ。ISBN  978-1-891389-45-0。
15. バルビエリ、チェーザレ（2007年）。『天文学の基礎』CRCプレス。132  ～ 135ページ。ISBN   978-0-7503-0886-1。
16. ヴァン・ヘルデン、A.（2010年）。『宇宙の測定：アリスタルコスからハレーまでの宇宙の次元』シカゴ大学出版局。第12章
17. "D". 『天文年鑑』. [国防総省] 海軍省、海軍天文台、航海年鑑事務所. 1981
18. 天文年鑑。[国防総省] 海軍省、海軍天文台、航海年鑑局。1981年、M10ページ。
19. アメリカ海軍天文台、航海年鑑局；イギリス、航海年鑑局（2006年）。天文年鑑補足。University Science Books。125ページ。ISBN  978-1-891389-45-0。
20. Gutzwiller, Martin C. (1998). 「月–地球–太陽：最古の三体問題」Reviews of Modern Physics . 70 (2): 589– 639. Bibcode :1998RvMP...70..589G. doi :10.1103/RevModPhys.70.589.
21. Webb, Stephen (1999), 「3.2 アリスタルコス、ヒッパルコス、プトレマイオス」『宇宙の測定：宇宙論的距離ラダー』Springer、 27– 35ページ 、 ISBN 9781852331061特に33ページを参照：「ヒッパルコスについて私たちが知っていることのほとんどすべては、プトレマイオスを通して私たちに伝わっている。」
22. Freedman, WL (2000). 「ハッブル定数と宇宙の膨張年齢」. Physics Reports . 333 (1): 13– 31. arXiv : astro-ph/9909076 . Bibcode : 2000PhR...333...13F. doi : 10.1016/S0370-1573(00)00013-2. S2CID  413222.
23. Al-Khalili, Jim (2010), Pathfinders: The Golden Age of Arabic Sc​​ience, Penguin UK, p. 270, ISBN 97801419650172015年3月17日にオリジナルからアーカイブ。地球と太陽の相対的な大きさの計算から、アリスタルコスは地球がはるかに大きな太陽の周りを回っている方が、その逆よりも理にかなっていると結論付けたのではないかと示唆する人もいます。
24. Whipple 2007, p. 47.
25. Newcomb, Simon (1911). "Parallax"  . In Chisholm, Hugh (ed.). Encyclopædia Britannica . Vol. 20 (11th ed.). Cambridge University Press. p. 761
26. ヒンクス、アーサー・R. (1909). 「太陽視差論文集 No. 7：1900年衝におけるエロスの写真赤経からの一般解」.王立天文学会月報. 69 (7): 544–67 .書誌コード: 1909MNRAS..69..544H. doi : 10.1093/mnras/69.7.544 .
27. ペリン、チャールズ・D. (1910).カリフォルニア大学リック天文台のクロスリー反射望遠鏡で撮影されたエロスの写真からの太陽視差の決定（初版）. ワシントンD.C.：ワシントン・カーネギー研究所. pp.  1– 104
28. Perrine, CD (1906). 「1900年にクロスリー反射望遠鏡で撮影されたエロスの写真の測定と縮小」太平洋天文学会刊行物. 18 (10): 226.
29. ペリン、チャールズ・D. (1908). 「クロスリー・エロス太陽視差研究の進展」.太平洋天文学会刊行物. 20 (120): 184.書誌コード: 1908PASP...20..184P. doi : 10.1086/121816 . S2CID  121782316.
30. キャンベル、WW (1906). 「天文台報告：リック天文台」.太平洋天文学会刊行物. 19 (113): 92.
31. の質量」. Mem. Roy. Astron. Soc . 66 : 11–66
32. 「天文定数」（PDF）。アメリカ海軍天文台。2011年7月20日時点のオリジナル（PDF）からアーカイブ。
33. の系統的定理のヒアデス星団への精密テスト」 。The Astrophysical Journal。515 (1): 256. arXiv : astro-ph/9808284 . Bibcode :1999ApJ...515..256N. doi :10.1086/307021. S2CID  15351552
34. Panagia, N.; Gilmozzi, R.; MacChetto, F.; Adorf, H.-M.; et al. (1991). 「SN 1987Aの星周リングの特性と大マゼラン雲までの距離」. The Astrophysical Journal . 380 : L23. Bibcode :1991ApJ...380L..23P. doi :10.1086/186164.
35. Rubin, JL (2015). 「相対論的局所化系からの相対論的五角座標と時空多様体の射影幾何学」. Electronic Journal of Theoretical Physics . 12 (32): 83– 112. 2015年2月8日時点のオリジナルからのアーカイブ
36. Popowski, P.; Gould, A. (1998). 「統計的視差と局所距離スケールの数学」arXiv : astro-ph/ 9703140
37. レイデン、アンドリュー・C; ハンソン、ロバート・B; ホーリー、スザンヌ・L; クレモラ、アーノルド・R; ハンリー、クリストファー・J (1996). 「統計視差によるRR Lyrae星の絶対等級と運動学」天文学ジャーナル. 112 : 2110. arXiv : astro-ph/9608108 . Bibcode :1996AJ....112.2110L. doi :10.1086/118167. S2CID  8732647.

その他の参考文献

• フレッド・L・ウィップル著 (2007).地球・月・惑星. Read Books. ISBN 978-1-4067-6413-0。
• マイケル・A・ザイリク著、ステファン・A・グレゴリー著 (1998).天文学と天体物理学入門（第4版）. Saunders College Publishing. ISBN 978-0-03-006228-5。