微分幾何学において、デュパンの指示線は曲面の局所的な形状を特徴付ける手法です。接平面に平行で、接平面から少し離れた平面 を描きます。この平面と曲面の交差を考えます。交差の形状はガウス曲率と関連しています。デュパンの指示線は、平面が接平面に近づくにつれて生じる極限過程の結果です。この指示線はシャルル・デュパンによって導入されました。
同様に、点pにおけるデュパンの指示線を描くこともできます。まず、曲面を回転・平行移動させ、pを原点とし、接平面をxy平面とします。すると、曲面の 等高線図はデュパンの指示線となります。
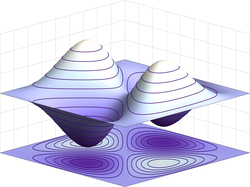
分類
ガウス曲率が正である楕円点の場合、交点は空になるか、閉曲線を形成する。極限において、この曲線は主方向と一致する楕円を形成する。曲率線は楕円の長軸と短軸を構成する。
特に、臍点の指示線は円です。
ガウス曲率が負の双曲点の場合、交点は双曲線を形成します。接平面の両側に2つの異なる双曲線が形成されます。これらの双曲線は同じ軸と漸近線を共有します。漸近線の方向は漸近方向と同じです。
特に、極小曲面上の各点の指示線は、2 つの曲率線とそれぞれ 45 度の角度を形成する、直角に交差する 2 本の線です。
放物点においてガウス曲率がゼロの場合、交点は2本の平行線を形成します。これらの2本の直線の方向は漸近方向と同じです。
特に、可展面上の各点の指示線は、母線に平行な 2 本の線です。
より複雑なケースでは、すべての2次導関数がゼロであるものの、高次導関数がゼロでない場合には、デュパンの示差曲線はより複雑になります。例えば、サルの鞍のデュパン示差曲線は、六芒双曲線の形をしています。
.png/1280px-Monkey_Saddle_Surface_(Shaded).png)
参照
参考文献
- アイゼンハート、ルーサー・P.（2004）『曲線と曲面の微分幾何学に関する論文』ドーバー、ISBN 04864382011909年の全文（現在は著作権切れ）
.png){kind=link}
