ファラデーのパラドックス

マイケル・ファラデー

ファラデーのパラドックス（ Faraday paradox）は、マイケル・ファラデーの電磁誘導の法則が誤った結果を予測するように見える 実験のことである。このパラドックスは2つの種類に分類される。

• ファラデーの法則は起電力(EMF)がゼロになると予測しているように見えますが、実際にはゼロではない EMF が存在します。
• ファラデーの法則は、EMF がゼロではないと予測しているように見えますが、実際には EMF はゼロです。

ファラデーは、1831年に最初の電磁発電機、つまりダイナモを発明した後、電磁誘導の法則を導き出しましたが、パラドックスに対する彼自身の説明には決して満足しませんでした。

ファラデーの法則とマクスウェル・ファラデー方程式の比較

ファラデーの法則（ファラデー・レンツの法則とも呼ばれる）は、起電力（EMF）は磁束の時間tに対する全微分によって与えられると述べています。

${\displaystyle {\mathcal {E}}=-{\frac {d\Phi _{B}}{dt}},}$

ここで、は起電力、Φ _Bはループ状の電線を流れる磁束です。起電力の方向はレンツの法則によって与えられます。見落とされがちな事実として、ファラデーの法則は磁束の偏微分ではなく全微分に基づいているという点があります。^{[ 1 ]}これは、表面を通る全磁束が一定であっても、起電力が発生する可能性があることを意味します。この問題を克服するために、特別な技術が用いられる場合があります。 「ファラデーの法則における特別な技術の使用」のセクションについては、以下を参照してください。 ${\displaystyle {\mathcal {E}}}$

しかし、ファラデーの法則の最も一般的な解釈は次のとおりです。

閉回路における誘導起電力は、回路内の磁束の時間変化率の負の値に等しい。 ^{[ 2 ] [ 3 ]}

このファラデーの法則は、閉回路が無限に細い電線のループである場合にのみ厳密に成立し、^{[ 4 ]}、他の状況では無効である。ファラデーの法則は磁束の偏微分ではなく全微分によって定義されるという事実、そしてEMFは必ずしも閉経路に限定されるわけではなく、後述するように放射状成分を持つ場合もあるという事実を無視している。異なるバージョンであるマクスウェル・ファラデーの方程式（後述）はあらゆる状況で有効であり、ローレンツ力の法則と組み合わせて用いることで、ファラデーの法則の正しい適用と整合する。

マクスウェル方程式とローレンツ力の法則からのファラデーの法則の証明の概要。

面積が である、移動する可能性のあるループを通る磁束の時間微分を考えます。 ${\displaystyle \Sigma (t)}$

${\displaystyle {\frac {d\Phi _{B}}{dt}}={\frac {d}{dt}}\int _{\Sigma (t)}\mathbf {B} (t)\cdot d\mathbf {A} }$

積分は、被積分関数が変化するか、積分領域が変化するという2つの理由により、時間の経過とともに変化します。これらは線形に加算されるため、次のようになります。

${\displaystyle \left.{\frac {d\Phi _{B}}{dt}}\right|_{t=t_{0}}=\left(\int _{\Sigma (t_{0})}\left.{\frac {\partial \mathbf {B} }{\partial t}}\right|_{t=t_{0}}\cdot d\mathbf {A} \right)+\left({\frac {d}{dt}}\int _{\Sigma (t)}\mathbf {B} (t_{0})\cdot d\mathbf {A} \right)}$

ここで、t ₀は任意の固定時間です。右辺第1項は変圧器の起電力、第2項は運動起電力に対応することを示します。右辺第1項は、マクスウェル・ファラデー方程式の積分形を用いて書き直すことができます。

${\displaystyle \int _{\Sigma (t_{0})}\left.{\frac {\partial \mathbf {B} }{\partial t}}\right|_{t=t_{0}}\cdot d\mathbf {A} =-\oint _{\partial \Sigma (t_{0})}\mathbf {E} (t_{0})\cdot d{\boldsymbol {\ell }}}$

速度vで移動しているときに、時間dtにおいて曲線∂Σのベクトル要素d ℓによって掃引される領域。

次に、右側の 2 番目の項を分析します。

${\displaystyle {\frac {d}{dt}}\int _{\Sigma (t)}\mathbf {B} (t_{0})\cdot d\mathbf {A} }$

これは証明の中で最も難しい部分です。より詳しい情報や別のアプローチについては参考文献を参照してください。^{[ 5 ] [ 6 ] [ 7 ]}ループが移動したり変形したりすると、表面が掃引されます（右の図を参照）。この掃引された表面を通る磁束は、ループに出入りする磁束に対応しており、したがって、これが時間微分に寄与する磁束です。（このステップでは、磁気に関するガウスの法則が暗黙的に使用されています。磁束線には始まりも終わりもないので、ワイヤに切断されることでのみループに入ることができます。）ループの小さな部分が短時間速度vで移動すると、ベクトル面積ベクトル が掃引されます。したがって、ここでのループを通る磁束の変化は ${\displaystyle d{\boldsymbol {\ell }}}$ ${\displaystyle dt}$ ${\displaystyle d\mathbf {A} =\mathbf {v} \,dt\times d{\boldsymbol {\ell }}}$

${\displaystyle \mathbf {B} \cdot (\mathbf {v} \,dt\times d{\boldsymbol {\ell }})=-dt\,d{\boldsymbol {\ell }}\cdot (\mathbf {v} \times \mathbf {B} )}$

したがって：

${\displaystyle {\frac {d}{dt}}\int _{\Sigma (t)}\mathbf {B} (t_{0})\cdot d\mathbf {A} =-\oint _{\partial \Sigma (t_{0})}(\mathbf {v} (t_{0})\times \mathbf {B} (t_{0}))\cdot d{\boldsymbol {\ell }}}$

ここで、vはループ上の点の速度です。 ${\displaystyle \partial \Sigma }$

これらをまとめると、

${\displaystyle \left.{\frac {d\Phi _{B}}{dt}}\right|_{t=t_{0}}=\left(-\oint _{\partial \Sigma (t_{0})}\mathbf {E} (t_{0})\cdot d{\boldsymbol {\ell }}\right)+\left(-\oint _{\partial \Sigma (t_{0})}(\mathbf {v} (t_{0})\times \mathbf {B} (t_{0}))\cdot d{\boldsymbol {\ell }}\right)}$

一方、起電力は、電線ループを一周する単位電荷あたりの利用可能なエネルギーとして定義されます。したがって、ローレンツ力の法則によれば、

${\displaystyle \mathrm {EMF} =\oint \left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)\cdot {\text{d}}{\boldsymbol {\ell }}}$

これらを組み合わせると、 ${\displaystyle {\frac {d\Phi _{B}}{dt}}=-\mathrm {EMF} }$

マクスウェル・ファラデー方程式は、時間変化する磁場は常に空間変化する非保存電場を伴い、その逆もまた同様であることを示すファラデーの法則を一般化したものであり、マクスウェル・ファラデー方程式は以下の通りである。

${\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}$

（SI単位系）ここでは偏微分演算子、は回転演算子、そしてE ( r , t ) は電場、B ( r , t ) は磁場です。これらの場は一般に、位置rと時間tの関数となります。 ${\displaystyle \partial }$ ${\displaystyle \nabla \times }$

マクスウェル・ファラデー方程式は4つのマクスウェル方程式の1つであり、古典電磁気学の理論において基本的な役割を果たしている。また、ケルビン・ストークスの定理によって積分形式で表すこともできる。^{[ 8 ]}

ファラデーの電磁誘導の法則は、EMFがゼロであると予測しているように見えるが、実際にはEMFがゼロではないと予測しているというパラドックス

これらのパラドックスは、ファラデーの法則で説明されるように回路内の磁束の変化によって、あるいは磁場中の導体の動きによって起電力が発生するという事実によって、一般的に解決されます。これはファインマンによって以下のように説明されています。A. ゾンマーフェルト著『Electrodynamics Academic Press 第3巻』362ページも参照。 ^{[ 9 ]}

機器

図1：ファラデーのディスク発電機。ディスクは角速度ωで回転し、永久磁石による静磁場B内で導体ディスクを円周方向に掃引します。磁気ローレンツ力v × Bによって電流が導体ディスクを横切って導体縁まで放射状に流れ、そこから回路は下部ブラシとディスクを支える軸を通って完了します。このように、機械的な運動によって電流が生成されます。

この実験には、いくつかのシンプルな部品が必要です（図1参照）。円筒形の磁石、導電性の縁を持つ導電性の円盤、導電性の軸、配線、そして検流計です。円盤と磁石は軸上に短い距離を置いて取り付けられ、軸上でそれぞれの対称軸を中心に自由に回転します。スライド式の接点を円盤の軸に、もう1つを縁に接続することで電気回路が形成されます。検流計を回路に挿入して電流を測定することができます。

手順

実験は次の 3 つのステップで進行します。

1. 磁石は回転しないように固定され、ディスクは軸を中心に回転します。その結果、検流計は直流電流を記録します。したがって、この装置は発電機として機能し、ファラデー発電機、ファラデーディスク、ホモポーラ（またはユニポーラ）発電機などと呼ばれます。
2. 磁石が軸を中心に回転する間、ディスクは静止した状態に保たれます。その結果、ガルバノメータは電流を検出しません。
3. ディスクと磁石を一緒に回転させます。ガルバノメータはステップ1と同様に電流を記録します。

なぜこれが逆説的なのでしょうか?

この実験は、一見するとファラデーの電磁誘導の法則に反するように見えるため、「パラドックス」と呼ぶ人もいます。なぜなら、円盤を流れる磁束は、回転しているものが何であっても同じように見えるからです。したがって、3つの回転ケースすべてにおいて、起電力はゼロになると予測されます。以下の議論は、この見方が磁束を計算する表面の選択ミスに起因することを示しています。

このパラドックスは、磁束線の観点から見ると少し異なるように見える。ファラデーの電磁誘導モデルでは、磁場は仮想的な磁束線で構成されており、これは紙に鉄粉をまぶして磁石の近くに置いたときに現れる磁束線に似ている。起電力は磁束線の切断速度に比例すると提案されている。磁束線が磁石から発生すると仮定すると、磁束線は磁石の座標系内で静止しており、磁石に対してディスクを回転させると（磁石を回転させるかディスクを回転させるかに関係なく）、起電力が発生するはずであるが、両方を同時に回転させると起電力は発生しないはずである。

ファラデーの説明

ファラデーの電磁誘導モデルでは、回路は磁束線を切断すると誘導電流を受け取ります。このモデルによれば、ファラデーディスクはディスクか磁石のどちらかが回転しているときにのみ動作するはずであり、両方が回転しているときには動作しないはずです。ファラデーは、磁石の回転時に磁界とその磁束線が静止していると仮定することで、観測結果との不一致を説明しようとしました（これは完全に正確な考え方ですが、磁束線モデルでは直感的ではないかもしれません）。言い換えれば、磁束線はそれぞれ独自の基準系を持っています。次のセクションで示すように、現代物理学（電子の発見以来）では磁束線モデルは必要なく、このパラドックスは解消されています。

現代的な説明

回路は必ずしもループではない

ステップ1では、パラドックスは容易に解決できます。この回路は、ファラデーの電磁誘導の法則が仮定するような単純なループではありません。電流がリムの両半分を流れるため、2つのループの結合体であると言えます（図2参照）。一方、半径接合部からブラシまでのリムの一部だけを残すと、回路全体が真のループとなり、その形状は時間とともに変化します。この場合、ファラデーの法則が適用され、正しい結果が得られます。

帰路を考慮する

ステップ2では、電流が観測されないため、磁場は回転する磁石と共に回転しなかったと結論付けられるかもしれません。（磁場が実質的に回転するか相対的に回転するかに関わらず、実験室系に対してvがゼロであるため、ローレンツ力はゼロです。したがって、実験室系から測定される電流は存在しません。）このパラドックスを説明するためにローレンツ方程式を用いたことで、磁場が磁石と共に回転するかどうかについて、文献において議論が巻き起こりました。ローレンツ方程式で表される電荷​​に対する力は、磁場（すなわち実験室系）とEMFが存在する導体との相対的な動きに依存するため、磁石がディスクと共に回転しても電圧が発生する場合、磁場（すなわち実験室系）は磁性体と共に回転しないはずである（もちろん、実験室系であるため）と推測されました。一方、磁場系の有効な定義、つまり「磁場の有効な／相対的な回転」は、導電性ディスクに対して相対的な動きを伴わずに回転します。

よく考えてみると、磁場が磁石とともに回転し、磁石がディスクとともに回転すると仮定した場合でも、電流はディスク内の起電力によってではなく（ディスクと磁石の間には相対運動がない）、ブラシを連結する外部回路によって生成されるはずである^{（[ 10 ] ）} 。この外部回路は実際には回転する磁石に対して相対運動している（ブラシは実験室のフレーム内にある）。

このメカニズムは、帰還経路に関する観察結果と一致しています。磁石の回転に関係なく、ディスクが帰還経路に対して移動すると常に EMF が生成されます。実際、ディスクと磁石の動きから誘導される EMF を電流ループを使用して測定する限り、磁場が磁石とともに回転するかどうかを判断できないことが示されています。(これは定義に依存し、場の動きは効果的/相対的にのみ定義できます。場のフラックスが物理的実体であるという見解を保持する場合、それは回転するか、またはそれがどのように生成されるかに依存します。ただし、これはローレンツの式で使用されるもの、特に測定が行われるフレームに対する電荷キャリアの速度vを変更するものではなく、場の強度は任意の時空点で相対性に応じて変化します。)

この問題を解決するために、静電測定や電子ビームを使用したいくつかの実験が提案されていますが、今のところ成功した例はありません。

ローレンツ力を利用する

運動中の荷電粒子（電荷q ）に働くローレンツ力F （瞬間速度v）。E場とB場は空間と時間によって変化する。

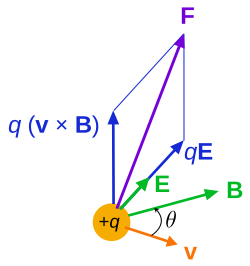
外部電場Eと磁場Bによって瞬間速度vを持つ電荷qの粒子に作用する力Fは、ローレンツ力によって与えられる。^{[ 11 ]}

${\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )}$

ここで×はベクトル積である。太字で書かれた量はすべてベクトルである。点電荷の相対論的に正しい電場は速度とともに次のように変化する： ^{[ 12 ]}

${\displaystyle \mathbf {E} ={\frac {q}{4\pi \epsilon _{0}}}{\frac {1-v^{2}/c^{2}}{(1-v^{2}\sin ^{2}\theta /c^{2})^{3/2}}}{\frac {\mathbf {{\hat {r}}'} }{|\mathbf {r} '|^{2}}}}$

ここで、は粒子の現在の（遅延のない）位置から磁場が測定されている点を指す単位ベクトルであり、θはと間の角度である。電荷の磁場Bは： ^{[ 12 ]}${\displaystyle \mathbf {\hat {r}} '}$ ${\displaystyle \mathbf {v} }$ ${\displaystyle \mathbf {r} '}$

${\displaystyle \mathbf {B} ={\frac {1}{c^{2}}}\mathbf {v} \times \mathbf {E} }$

最も基本的なレベルでは、ローレンツ力の合計は、他のすべての電荷に作用するすべての電荷の 電場Eと磁場Bの累積結果です。

磁石は回転しているが、磁束線は静止しており、導体は静止している

円筒状の導体ディスクが静止している一方、円筒状の磁気ディスクが回転している特殊なケースを考えてみましょう。このような状況では、導体ディスク内の電荷の平均速度vは初期値でゼロであり、したがって磁力F = q v × Bは0となります。ここで、vは測定が行われる座標系に対する回路上の電荷qの平均速度、 qは電子の電荷です。

磁石と磁束線が静止し、導体が回転している場合

電子とそれに作用する力の発見後、このパラドックスを微視的に解明することが可能になりました。図1をご覧ください。装置の金属部分は導電性を持ち、電子の運動による電流を金属境界内に閉じ込めます。磁場中を移動するすべての電子は、 F = q v × Bのローレンツ力を受けます。ここで、vは測定が行われる座標系に対する電子の相対速度、qは電子の電荷です。「電磁場の座標系」のような座標系は存在しないことを覚えておいてください。座標系は特定の時空点に設定されるものであり、数学的対象としての拡張場や磁束線ではありません。磁束を物理的実体として考える場合（磁束量子を参照）、または場の運動／回転の有効／相対的な定義を考える場合（下記参照）は、別の問題となります。このメモは、このパラドックスを解決するのに役立ちます。

ローレンツ力は、ディスク面内の電子の速度と、ディスクに垂直（面法線）な磁場の両方に垂直です。ディスクの座標系内で静止している電子は、B磁場（つまり回転軸、あるいは実験室座標系。上記の注釈を思い出してください）に対してディスクと共に円運動するため、放射状のローレンツ力を受けます。図1では、この力（電子ではなく正電荷に作用する力）は、右手の法則に従って縁に向かって外側に向いています。

もちろん、電流の原因となるこの放射状の力は、電子速度の放射状成分を作成し、今度は電子の円運動に反対する独自のローレンツ力成分を生成し、ディスクの回転を遅くする傾向がありますが、電子は円運動の成分を保持し、放射状のローレンツ力を介して電流を駆動し続けます。

ファラデーの法則を用いた特殊技術の使用

リムのブラシから外側のループ、そして軸を通りディスクの中心に至る経路の部分を通る磁束は常にゼロです。これは、磁場がこの経路の平面内にあるため（経路に垂直ではないため）、回転するものに関わらず、この経路の部分の積分起電力は常にゼロになるからです。したがって、軸からディスクを横切り、リムのブラシに至る経路の部分に注目します。

ファラデーの電磁誘導の法則は次のように表現できる。^{[ 13 ]}

あらゆる閉回路における誘導起電力または EMF は、回路を通る磁束の時間変化率に等しくなります。

数学的には、この法則は次のように述べられます。

${\displaystyle {\mathcal {E}}=-{\frac {d\Phi _{B}}{dt}}=-{\frac {d}{dt}}\iint _{\Sigma (t)}d\mathbf {A} \cdot \mathbf {B} (\mathbf {r} ,\ t)\ ,}$

ここで、Φ _Bは磁束、d AはEMF が検出されるループによって囲まれた 移動表面Σ ( t )の面積のベクトル要素です。

図2：起電力を求めるための2つのループ。幾何学的に単純な経路は使いやすいが、もう1つは同じ起電力を与える。どちらも物理的な電流の流れを模倣するものではない。

この法則は、磁束鎖交が単に B フィールドとディスクの面積を掛け合わせたものになるファラデー ディスク ジェネレータとどのように関連しているのでしょうか。

一つのアプローチは、「鎖交磁束の変化率」という概念を定義することです。これは、ブラシから軸までディスクを横切る仮想的な線を引き、単位時間あたりにこの線を通過する鎖交磁束の量を問うことによって行われます。図2を参照してください。ディスクの半径をRとすると、中心角θを持つディスクの扇形の面積は次のようになります 。

${\displaystyle A={\frac {\theta }{2\pi }}\pi R^{2}\ ,}$

したがって、磁束が仮想線を通過する速度は

${\displaystyle {\mathcal {E}}=-{\frac {d\Phi _{B}}{dt}}=B{\frac {dA}{dt}}=B\ {\frac {R^{2}}{2}}\ {\frac {d\theta }{dt}}=B\ {\frac {R^{2}}{2}}\omega \ ,}$

ここで、ω = dθ / dt は回転角速度です。符号はレンツの法則に基づいて決定されます。つまり、運動によって発生する磁場は、回転によって引き起こされる磁束の変化に逆らわなければなりません。例えば、図2の放射状セグメントを持つ回路は、右手の法則に従って、印加磁場を増加させ、磁束鎖交数を増加させる傾向があります。これは、この経路を通る磁束が回転によって減少していることを示唆しており、dθ / dtは負です。

EMFのこの磁束切断の結果は、半径rにおけるローレンツ力/単位電荷、すなわち| v × B | = Bv = Brωを使用して、微小な試験電荷が仮想線を横切るときに単位電荷あたりに行われる仕事を計算することと比較できます。

${\displaystyle {\mathcal {E}}=\int _{0}^{R}drBr\omega ={\frac {R^{2}}{2}}B\omega \ ,}$

同じ結果になります。

回路によって切断される磁束を求める上記の方法は、境界面 Σ( t ) の時間微分を適切に扱うことで、磁束法則として形式化されます。もちろん、時間依存の極限を持つ積分の時間微分は、単に被積分関数の時間微分のみを積分したものではありません。この点はしばしば忘れられがちです。ライプニッツの積分則とローレンツ力を参照してください。

Σ( t )面を選択する際の制約は、(i) EMF が求められる閉曲線で囲まれている必要があること、および (ii) 回路のすべての可動部分の相対運動を捉える必要があることです。境界曲線が電流の物理的な流れの線と一致する必要はまったくありません。一方、誘導は相対運動に関するものであり、経路はあらゆる相対運動を捉える必要があります。図 1 のように、電流経路の一部が空間領域に分布している場合、電流を駆動する EMF はさまざまな経路を使用して求めることができます。図 2 は 2 つの可能性を示しています。すべての経路には明らかな戻りループが含まれますが、ディスクには 2 つの経路が示されています。1 つは幾何学的に単純な経路で、もう 1 つは曲がりくねった経路です。任意の経路を自由に選択できますが、許容される経路の一部はディスク自体に固定され、ディスクとともに回転します。磁束は経路全体、戻りループ、およびディスク セグメントを通じて計算され、その変化率が求められます。

図3：ファラデーディスクをスライドする導電性の長方形にマッピングした例。ディスクは環状体として捉えられ、半径に​​沿って切断され、長方形になるように折り曲げられる。

この例では、これらすべての経路は同じ磁束変化率、つまり同じ起電力（EMF）につながります。この経路の独立性についての直感的な理解を深めるために、図 3 ではファラデー ディスクをストリップ上に展開し、滑走する長方形の問題に似せています。滑走する長方形の場合、長方形内の電流のパターンは時間に依存せず、したがって回路を結ぶ磁束の変化率とは無関係であることが明らかになります。電流が長方形（またはディスク）をどのように横切るかを正確に考慮する必要はありません。長方形の上部と下部（ディスク内の軸からブラシまで）を結び、長方形とともに移動する（ディスクとともに回転する）経路のいずれを選択しても、同じ磁束変化率が得られ、同じ起電力が予測されます。ディスクの場合、この磁束変化率の推定は、ブラシと軸を結ぶ線をディスクが回転して通過することに基づいて上記で行った推定と同じです。

リターンパスを使用した構成

この解析では、磁石が「動いている」かどうかは、帰還路に誘起される磁束のため、無関係です。重要な相対運動は、ディスクと帰還路の運動であり、ディスクと磁石の運動ではありません。これは、帰還路が導線ではなく別のディスクである改良型ファラデーディスクを使用するとより明確になります。つまり、2枚の導電性ディスクを同じ軸上に隣接させて設置し、中心と円周で電気的な滑り接触を生じさせます。電流は2枚のディスクの相対回転に比例し、磁石の回転とは無関係になります。

リターンパスのない構成

ファラデーディスクは、検流計も帰還路も必要とせずに動作させることもできます。ディスクが回転すると、電子は縁に沿って集まり、軸付近に欠損を残します（あるいはその逆）。原理的には、例えば縁と軸の間に発生する起電力を通して電荷分布を測定することが可能です（ただし、必ずしも容易ではありません）。この電荷の分離は、ディスクと磁石の相対回転速度に比例します。

ファラデーの電磁誘導の法則は、EMFがゼロではないと予測しているように見えるが、実際にはEMFがゼロであると予測するパラドックス

これらのパラドックスは、通常、回路の見かけ上の動きが実際には回路の分解と、それに続く別の経路での回路の再構築であると判断することによって解決されます。

追加のルール

Tilley 実験用の回路。

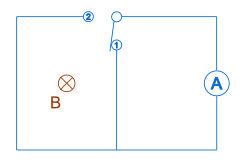
ディスクだけが回転する場合、回路を流れる磁束に変化はありませんが、ファラデーの法則に反して起電力が誘導されます。磁束に変化があるが誘導電圧がない例も示すことができます。図 5 (右の近く) は、ティリーの実験で使用されたセットアップを示しています。^{[ 14 ]}これは 2 つのループまたはメッシュを持つ回路です。右側のループには検流計が接続され、左側のループの中央には磁石、左側のループにはスイッチ、ループ間にスイッチがあります。最初は左側のスイッチが開いていて、右側のスイッチが閉じています。左側のスイッチが閉じていて、右側のスイッチが開いている場合、磁石の場には変化がありませんが、検流計回路の面積が変化します。これは、磁束に変化があることを意味します。しかし、検流計は偏向しなかったので、誘導電圧はなく、ファラデーの法則はこの場合は適用されません。 AGケリーによれば、これはファラデーの実験における誘導電圧は、磁束線による回路の「切断」によるものであり、「磁束の鎖交」、つまり磁束の実際の変化によるものではないことを示唆している。これはティリーの実験からも導かれる。なぜなら、回路を横切る磁力線の動きはなく、したがって回路を通る磁束の変化はあるものの、誘導電流は発生しないからである。ヌスバウムは、ファラデーの法則が成立するためには、磁束の変化を生み出すために仕事が行われなければならないと示唆している。^{[ 15 ]} この考えを理解するために、ヌスバウムの議論を段階的に見ていこう。^{[ 15 ]}まず、2本の電流を流す電線間の力を計算する。電線1が電線2から受ける力は、次のように表される。

${\displaystyle \mathbf {F} _{21}={\frac {\mu _{0}}{4\pi }}I_{1}I_{2}\oint _{C_{1}}\oint _{C_{2}}{\frac {d\mathbf {l_{1}} \ \mathbf {\times } \ (d\mathbf {l_{2}} \ \mathbf {\times } \ {\hat {\mathbf {r} }}_{21})}{r_{21}^{2}}}}$

2 番目のワイヤからの磁場は次のように表されます。

${\displaystyle \mathbf {B} _{2}={\frac {\mu _{0}}{4\pi }}I_{2}\oint _{C_{2}}{\frac {(d\mathbf {l_{2}} \ \mathbf {\times } \ {\hat {\mathbf {r} }}_{21})}{r_{21}^{2}}}}$

したがって、ワイヤ 1 にかかる力は次のように書き直すことができます。

${\displaystyle \mathbf {F} _{21}=I_{1}\oint _{C_{1}}d\mathbf {l_{1}} \ \mathbf {\times } \mathbf {B} _{2}}$

ここで、一定磁場中で 変位する導体片を考えてみましょう。この導体片が行う仕事は次式で求められます。${\displaystyle d\mathbf {l} }$ ${\displaystyle d\mathbf {r} }$

${\displaystyle dW=d\mathbf {F} \cdot d\mathbf {r} }$

先ほど調べた結果を代入すると次のようになります。 ${\displaystyle d\mathbf {F} }$

${\displaystyle dW=(Id\mathbf {l} \mathbf {\times } \mathbf {B} )\cdot d\mathbf {r} }$

導体の変位によってカバーされる領域は次のとおりです。

${\displaystyle d\mathbf {S} =d\mathbf {r} \mathbf {\times } d\mathbf {l} }$

したがって：

${\displaystyle dW=I\mathbf {B} \cdot d\mathbf {S} =Id\Phi _{B}}$

微分仕事は電荷と電位差で表すこともできます。 ${\displaystyle dq}$ ${\displaystyle V}$

${\displaystyle dW=Vdq=VIdt}$

微分仕事の 2 つの方程式を等しく設定すると、ファラデーの法則に到達します。

${\displaystyle d\Phi _{B}=Vdt}$

さらに、これは がゼロでない場合にのみ成り立つことがわかります。つまり、ファラデーの法則は、磁束の変化をもたらすために仕事が行われた場合にのみ有効です。 ${\displaystyle dW}$

このような状況でファラデーの法則を検証する数学的な方法は、ファラデーの電磁誘導の法則の証明のようにEMFの定義を一般化することです。

${\displaystyle \mathrm {EMF} =\oint \left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)\cdot d{\boldsymbol {\ell }}}$

ガルバノメータは通常、回路の電流に寄与する EMF の第 1 項のみを測定しますが、第 2 項がガルバノメータが運動 EMF として測定する電流の一部に寄与する場合など、第 2 項の組み込みを測定できる場合もあります (例: ファラデーのディスク実験)。 上記の状況では、第 1 項はゼロであり、第 1 項のみがガルバノメータが測定する電流を導くため、誘導電圧はありません。 ただし、EMF の上記の一般化では磁束の見かけの変化が第 2 項に移動するため、ファラデーの法則は依然として有効です。 ただし、それはガルバノメータによって測定されません。 は回路上の点の局所速度であり、電荷キャリアではないことに注意してください。 結局のところ、これらすべての状況は、相対性理論と物質の微細構造、および/またはマクスウェル方程式とローレンツの公式の完全性、またはそれらの組み合わせであるハミルトン力学の懸念と一致しています。 ${\displaystyle \mathbf {v} }$

参照

• ファラデーの電磁誘導の法則
• ローレンツ力
• 動く磁石と導体の問題
• 共回転電場

参考文献

1. Crooks, MJ; Litvin, DB; Matthews, PW; Macaulay, R.; Shaw, J. (1978-07-01). 「一体型ファラデー発電機：1851年の逆説的な実験」（PDF） .ペンシルベニア州立大学.
2. 「ファラデーの法則は、閉路周囲の起電力は、その閉路に囲まれた磁束の時間変化率の負の値に等しいと述べている」ジョーダン、エドワード、バルメイン、キース・G. (1968). 『電磁波と放射システム』（第2版）プレンティス・ホール、100ページ。
3. であるあらゆる表面を通過する磁束である」ウィリアム・ヘイト（1989年）『電磁気工学』（第5版）マグロウヒル社、  312ページ。ISBN 0-07-027406-1。
4. 「磁束則」とは、磁束と起電力の関係を示す法則をファインマンが用いた用語である。リチャード・フィリップス・ファインマン、レイトン・RB、サンズ・ML (2006). 『ファインマン物理学講義』サンフランシスコ：ピアソン/アディソン・ウェスレー。第2巻、17～12ページ。ISBN 0-8053-9049-9。
5. Davison, ME (1973). 「Bが時間に依存しないとき、ローレンツ力の法則がファラデーの電磁誘導法則を暗示することの簡単な証明」アメリカ物理学ジャーナル. 41 (5): 713. Bibcode : 1973AmJPh..41..713D . doi : 10.1119/1.1987339 .
6. クレイとオーウェン著『基礎理論物理学：簡潔な概要』p155、 Googleブックスリンク
7. K. Simonyi、Theoretische Elektrotechnik、第 5 版、 VEB Deutscher Verlag der Wissenschaften、ベルリン、1973 年、方程式 20、47 ページ
8. ロジャー・F・ハリントン(2003).電磁気工学入門. ミネオラ, ニューヨーク州: ドーバー出版. p. 56. ISBN 0-486-43241-6。
9. 「電気力学講義第362巻」 1952年。
10. AG Kelly, アイルランド技術者協会モノグラフ5 & 6, 1998, ISBN 1-898012-37-3およびISBN 1-898012-42-3]
11. ジャクソンの 2 ページを参照してください。この本では、4 つの現代のマクスウェル方程式が列挙され、次のように述べられています。「荷電粒子の運動を考慮する上で、点電荷qに作用する力を表すローレンツ力方程式F = q ( E + v × B )も不可欠です。」
12. グリフィス, デイビッド・J. (1998). 『電気力学入門（第3版）』 プレンティス・ホール. pp.  222–224, 435–440 . ISBN 0-13-805326-X。
13. 例えば、 MNO Sadiku (2007). Elements of Electromagnetics (Fourth ed.). NY/Oxford UK: Oxford University Press. pp. §9.2 pp. 386 ff. ISBNを参照。 978-0-19-530048-2。
14. デラウェア州ティリー、午前。 Ｊ．Ｐｈｙｓ． 36、458 (1968)
15. ヌスバウム, A.、「ファラデーの法則のパラドックス」、http://www.iop.org/EJ/article/0031-9120/7/4/006/pev7i4p231.pdf? request-id=49fbce3f-dbc4-4d6c-98e9-8258814e6c30

さらに読む

• マイケル・ファラデー『電気の実験的研究』第1巻、第1集、1831年、RMハッチンズ編『西洋世界の偉大な書』第45巻、Encyclopædia Britannica, Inc.、シカゴ大学、1952年。[1]
• 電磁誘導：マクスウェルの一般法則に取って代わった「磁束則」ジュゼッペ・ジュリアーニ著 - ベクトルポテンシャルを用いた電磁誘導の法則
• 「ホモポーラ電気ダイナモ」 – ファラデーディスクの起電力の方程式の導出が含まれています
• ドン・ランカスターの「Tech Musings」コラム、1998年2月– ファラデーディスクの実際的な非効率性について
• 「ファラデーの最後の謎：磁場は磁石とともに回転するのか？」（PDF） - 逆説的な理論だが、ファラデーの実験に関する有用な参考文献が含まれている。
• PJ Scanlon、RN Henriksen、JR Allen、「電磁誘導へのアプローチ」、Am. J. Phys. 37、698–708 (1969)。 – ファラデーの法則をファラデーディスクに適用する方法を説明します。
• ホルヘ・グアラ＝バルベルデ、ペドロ・マッツォーニ、リカルド・アキレス「ホモポーラモーター：真の相対論的エンジン」Am. J. Phys. 70 (10), 1052–1055 (2002年10月)。 – ファラデーディスクを説明できるのはローレンツ力のみであると主張し、その実験的証拠をいくつか示している。
• Frank Munley, Challenges to Faraday's flux rule, Am. J. Phys. 72, 1478 (2004). – 上記のScanlon参考文献の概念に関する最新の議論。
• リチャード・ファインマン、ロバート・レイトン、マシュー・サンズ共著、『ファインマン物理学講義 第2巻』第17章 – ファラデーの「パラドックス」（磁束は変化しないが起電力が誘起される）に加えて、磁束は変化するが起電力は誘起されない「ロッキングプレート」実験についても解説している。彼は、ローレンツ力とマクスウェル・ファラデー方程式（引用欄参照）の組み合わせによって常に正しい物理法則が導かれることを示し、これら2つの「パラドックス」を自ら提起している。