| フォスターグラフ | |
|---|---|
 フォスターグラフ | |
| 名前の由来 | ロナルド・マーティン・フォスター |
| 頂点 | 90 |
| エッジ | 135 |
| 半径 | 8 |
| 直径 | 8 |
| 胴回り | 10 |
| 自己同型 | 4320 |
| 彩色数 | 2 |
| 色指数 | 3 |
| キュー番号 | 2 |
| プロパティ | 立方二 部 対称 ハミルトニアン 距離推移 |
| グラフとパラメータの表 | |
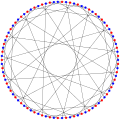
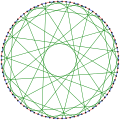
数学のグラフ理論の分野において、フォスターグラフは90の頂点と135の辺を持つ二部3正則グラフである。 [1]
フォスターグラフはハミルトングラフであり、彩色数2、彩色指数3、半径8、直径8、内周10である。また、3頂点連結、3辺連結のグラフである。キュー数は2で、本の厚さの上限は4である。[2]
立方 距離正則グラフはすべて知られている。[3]フォスターグラフはそのようなグラフ13個のうちの1つである。これは交差配列{3,2,2,2,2,1,1,1;1,1,1,1,2,2,2,3}を持つ唯一の距離推移グラフである。 [4]これは、一般化四角形GQ (2,2)の8角形を含まない唯一の三重被覆である部分線形空間の接続グラフとして構成できる。このグラフは、立方対称グラフのフォスター調査にこのグラフが含まれていた RMフォスターにちなんで名付けられた。
フォスターグラフの二部グラフは、距離正則グラフであり、かつ局所線形グラフである。これは、次数6のそのようなグラフの有限個の1つである。[5]
代数的性質
フォスターグラフの自己同型群は位数4320の群である。[6]この群はグラフの頂点、辺、弧に対して推移的に作用する。したがって、フォスターグラフは対称グラフである。任意の頂点から任意の頂点へ、任意の辺から任意の辺へ、自己同型を持つ。フォスター調査によると、F90Aと呼ばれるフォスターグラフは、90頂点を持つ唯一の立方対称グラフである。[7]
フォスターグラフの特性多項式は に等しい。
ギャラリー
参考文献
- ^ Weisstein, Eric W.「フォスターグラフ」。MathWorld。
- ^ Wolz, Jessica; SATを用いた線形レイアウトのエンジニアリング。修士論文、テュービンゲン大学、2018年
- ^ ブラウワー、AE;午前、コーエン。 Neumaier、A. 距離正規グラフ。ニューヨーク: Springer-Verlag、1989 年。
- ^ 立方距離正則グラフ、A. Brouwer。
- ^ 平木 明; 野村 一正; 鈴木 博 (2000) 「価数6との距離正則グラフ」, Journal of Algebraic Combinatorics , 11 (2): 101– 134, doi : 10.1023/A:1008776031839 , MR 1761910
- ^ 「G-12 フォスターグラフ」、グラフ百科事典、 2024年2月26日閲覧。
- ^ Conder, M.および Dobcsányi, P. 「768 頂点までの三価対称グラフ」 J. Combin. Math. Combin. Comput. 40, 41-63, 2002.
- Biggs, NL; Boshier, AG; Shawe-Taylor, J. (1986)、「立方距離正則グラフ」、ロンドン数学会誌、33 (3): 385– 394、doi :10.1112/jlms/s2-33.3.385、MR 0850954。
- Van Dam, Edwin R.; Haemers, Willem H. (2002)、「いくつかの距離正則グラフのスペクトル特性」、Journal of Algebraic Combinatorics、15 (2): 189– 202、doi : 10.1023/A:1013847004932、MR 1887234。
- ヴァン・マルデゲム、ヘンドリック(2002)、「三価距離正則グラフからの10の例外的幾何学」、Annals of Combinatorics、6(2):209-228、doi:10.1007/PL00012587、MR 1955521、S2CID 195315348。