グラフ一覧

この部分的なグラフの一覧には、グラフとグラフ族の定義が含まれています。頂点やパスなど、個々のグラフの種類に言及しないグラフ理論用語の定義については、「グラフ理論用語集」を参照してください。特定の種類のグラフに関する既存の記事へのリンクについては、「カテゴリ:グラフ」を参照してください。グラフ理論で考慮される有限構造の中には、グラフの位相に由来するものや発見者にちなんで名付けられているものがあります。有名な例としては、ピーターセングラフがあります。これは10頂点の具体的なグラフで、様々な文脈で最小限の例または反例として現れます。

個別のグラフ

• 
  バラバン10ケージ
• 
  バラバン11ケージ
• 
  ビディアキスキューブ
• 
  ブリンクマングラフ
• 
  ブルグラフ
• 
  バタフライグラフ
• 
  Chvátalグラフ
• 
  ダイヤモンドグラフ
• 
  デューラーグラフ
• 
  エリンガム・ホートン54グラフ
• 
  エリンガム・ホートン78グラフ
• 
  エレラグラフ
• 
  フランクリングラフ
• 
  フルクトグラフ
• 
  ゴールドナー・ハラリーグラフ
• 
  ゴロムグラフ
• 
  グロッチュグラフ
• 
  ハリーズグラフ
• 
  ハリーズ・ウォングラフ
• 
  ハーシェルグラフ
• 
  ホフマングラフ
• 
  ホルトグラフ
• 
  ホートングラフ
• 
  キッテルグラフ
• 
  マルクストロームグラフ
• 
  マギーグラフ
• 
  メレディスグラフ
• 
  モーザースピンドル
• 
  スースリエグラフ
• 
  プッサングラフ
• 
  ロバートソングラフ
• 
  シルベスターグラフ
• 
  トゥッテの断片
• 
  トゥッテグラフ
• 
  ヤング・フィボナッチグラフ
• 
  ワグナーグラフ
• 
  ウェルズグラフ
• 
  ウィーナー・アラヤグラフ
• 
  風車グラフ

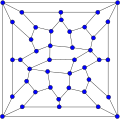
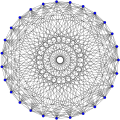
高度に対称的なグラフ

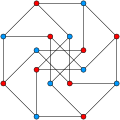
強正則グラフ

v頂点とランクkの強正則グラフは通常、srg( v,k ,λ,μ) と表記されます。

• 
  クレプシュグラフ
• 
  キャメロングラフ
• 
  ピーターセングラフ
• 
  ホール・ヤンコグラフ
• 
  ホフマン・シングルトングラフ
• 
  ヒグマン・シムズグラフ
• 
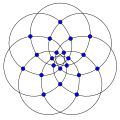
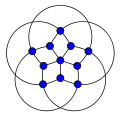
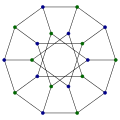
  13次のペイリーグラフ
• 
  シュリカンデグラフ
• 
  シュレーフリグラフ
• 
  ブラウワー・ヘーマーズグラフ
• 
  局所マクラフリングラフ
• 
  パーケルグラフ
• 
  ゲヴィルツグラフ

対称グラフ

対称グラフとは、隣接する頂点の任意の順序付き対が他の任意の順序付き対に対称性（グラフの自己同型性）を持つグラフです。フォスター・センサスは、すべての小さな対称3-正則グラフをリストアップしています。すべての強正則グラフは対称ですが、その逆は成り立ちません。

• 
  ヒーウッドグラフ
• 
  メビウス・カントールグラフ
• 
  パップスグラフ
• 
  デザルググラフ
• 
  ナウルのグラフ
• 
  コクセターグラフ
• 
  タット・コクセターグラフ
• 
  ディックグラフ
• 
  クライングラフ
• 
  フォスターグラフ
• 
  ビッグス・スミスグラフ
• 
  ラドグラフ​

半対称グラフ

• 
  フォークマングラフ
• 
  灰色のグラフ
• 
  リュブリャナグラフ
• 
  トゥッテ 12ケージ

グラフファミリー

完全グラフ

頂点上の完全グラフはしばしば-クリークと呼ばれ、ドイツ語のkomplettに由来して と表記される。^[1]${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle K_{n}}$

• 
  ${\displaystyle K_{1}}$
• 
  ${\displaystyle K_{2}}$
• 
  ${\displaystyle K_{3}}$
• 
  ${\displaystyle K_{4}}$
• 
  ${\displaystyle K_{5}}$
• 
  ${\displaystyle K_{6}}$
• 
  ${\displaystyle K_{7}}$
• 
  ${\displaystyle K_{8}}$

完全二部グラフ

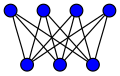
完全二部グラフは通常 と表記されます。スターグラフのセクションを参照してください。このグラフは、以下で紹介する4-閉路（正方形）に相当します。 ${\displaystyle K_{n,m}}$ ${\displaystyle n=1}$ ${\displaystyle K_{2,2}}$ ${\displaystyle C_{4}}$

• 
  ${\displaystyle K_{2,3}}$
• 
  ${\displaystyle K_{3,3}}$ 、ユーティリティグラフ
• 
  ${\displaystyle K_{2,4}}$
• 
  ${\displaystyle K_{3,4}}$

サイクル

頂点上の循環グラフはn-循環グラフと呼ばれ、通常は と表記されます。これは巡回グラフ、多角形、またはn角形とも呼ばれます。特殊な例としては、三角形、正方形、そしてギリシャ語で五角形、六角形など と呼ばれるものがあります。${\displaystyle n}$ ${\displaystyle C_{n}}$ ${\displaystyle C_{3}}$ ${\displaystyle C_{4}}$ ${\displaystyle C_{5}}$ ${\displaystyle C_{6}}$

• 
  ${\displaystyle C_{3}}$
• 
  ${\displaystyle C_{4}}$
• 
  ${\displaystyle C_{5}}$
• 
  ${\displaystyle C_{6}}$

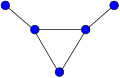
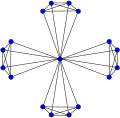
友情グラフ

友情グラフ Fn_{は、サイクル}グラフC3のn個のコピーを共通の頂点で結合することによって構築できます。 ^[2]

友情グラフF ₂、F ₃、F ₄。

フラーレングラフ

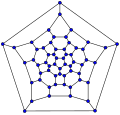
グラフ理論において、フラーレンとは、すべての面のサイズが5または6（外面を含む）である多面体グラフのことです。オイラーの多面体公式V − E  +  F  = 2 （ここでV  、  E、Fは頂点、辺、面の数）から、フラーレンにはちょうど12個の五角形とh  =  V /2 − 10個の六角形が存在することがわかります。したがって、V =  20 + 2 h、E  = 30 + 3 hとなります。フラーレングラフは、対応するフラーレン化合物の シュレーゲル表現です。

• 
  20フラーレン（十二面体グラフ）
• 
  24-フラーレン（六角形切頂台形グラフ）
• 
  26フラーレングラフ
• 
  60-フラーレン（切頂二十面体グラフ）
• 
  70-フラーレン

与えられた数の六角形面を持つすべての非同型フラーレンを生成するアルゴリズムは、G. BrinkmannとA. Dressによって開発されました。^[3] G. Brinkmannはfullgenと呼ばれる無料で利用可能な実装も提供しました。

プラトン立体

4頂点の完全グラフは正四面体の骨格を形成し、より一般的には完全グラフは単体の骨格を形成します。超立方体グラフは、高次元正多面体の骨格でもあります。

• 
  キューブ、
  ${\displaystyle n=8}$ ${\displaystyle m=12}$
• 
  八面体、
  ${\displaystyle n=6}$ ${\displaystyle m=12}$
• 
  十二面体、
  ${\displaystyle n=20}$ ${\displaystyle m=30}$
• 
  二十面体、
  ${\displaystyle n=12}$ ${\displaystyle m=30}$

切頂立体

• 
  切頂四面体
• 
  切り取られた立方体
• 
  切頂八面体
• 
  切頂十二面体
• 
  切頂二十面体

スナークス

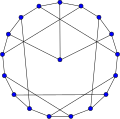
スナークとは、任意の適切な辺彩色において4色が必要となる、橋のない 立方グラフです。最小のスナークは、既に上で挙げた ピーターセングラフです。

• 
  Blanuša snark (first)
• 
  Blanuša snark (2番目)
• 
  二重星の皮肉
• 
  花のスナーク
• 
  ルペキンの皮肉（初）
• 
  ルペキンの皮肉（2番目）
• 
  シェケレスの皮肉
• 
  ティーツェグラフ
• 
  ワトキンスの皮肉

星

スターS _kは完全二部グラフK _{1, k}です。スターS 3_はクローグラフと呼ばれます。

スターグラフS ₃、S ₄、S ₅、S ₆。

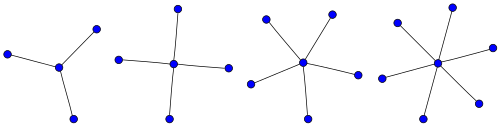
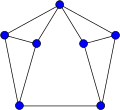
ホイールグラフ

ホイールグラフ Wn_は、( n  −1)サイクル 内のすべての頂点に1つの頂点を接続することによって構築されるn頂点のグラフです。

ホイール– 。${\displaystyle W_{4}}$ ${\displaystyle W_{9}}$

その他のグラフ

この部分的なリストには、特定の名前で知られているが、Wikipedia に独自の記事がないグラフとグラフ ファミリの定義が含まれています。

ギヤ

G4_​

ギアグラフ（G _nと表記）は、ホイールグラフ （W _{n ）}の外周上の隣接する頂点間に頂点を1つずつ追加することで得られるグラフです。したがって、G _{n は}2 n +1個の頂点と3 n個の辺を持ちます。^[4]ギアグラフはスクエアグラフ（正方グラフ）の例であり、スクエアグラフの禁制グラフ特性において重要な役割を果たします。^[5]ギアグラフは歯車（cogwheels）や二部車輪（bipartite wheels）とも呼ばれます。

舵

ヘルムグラフ（Hnと表記）は、_ホイールグラフ Wn_の外側の回路の各ノードに1つのエッジとノードを接続することによって得られるグラフである。^{[6] [7]}

ロブスター

ロブスターグラフは、すべての頂点が中心パスから距離2以内にある木です。 [ ^{8] [9]}キャタピラー と比較してください。

ウェブ

ウェブグラフW _4,2は立方体です。

ウェブグラフW _{n , r}は、サイクルグラフC n_のr 個の同心円状のコピーから構成されるグラフであり、対応する頂点は「スポーク」で接続されています。したがって、W _{n ,1は}C _nと同じグラフであり、W _n,2はプリズムです。

ウェブグラフは、外側のサイクルのエッジを削除したプリズムグラフYn _{+ 1,3}^{としても定義されています。 [7] [10]}

参考文献

1. David GriesとFred B. Schneider、「離散数学への論理的アプローチ」、Springer、1993年、436ページ。
2. Gallian, JA「Dynamic Survey DS6: Graph Labeling」Electronic Journal of Combinatorics、DS6、1-58、2007年1月3日。[1] 2012年1月31日にWayback Machineにアーカイブ。
3. ブリンクマン、グンナー；ドレス、アンドレアスWM (1997). 「フラーレンの構成的列挙」.アルゴリズムジャーナル. 23 (2): 345– 358. doi :10.1006/jagm.1996.0806. MR  1441972.
4. Weisstein, Eric W.「ギアグラフ」。MathWorld。
5. Bandelt, H.-J.; Chepoi, V.; Eppstein, D. (2010)「有限および無限平方グラフの組合せ論と幾何学」、SIAM Journal on Discrete Mathematics、24 (4): 1399– 1440、arXiv : 0905.4537、doi :10.1137/090760301、S2CID  10788524
6. Weisstein, Eric W.「ヘルムグラフ」。MathWorld。
7. 「アーカイブコピー」（PDF） 。 2012年1月31日時点のオリジナル（PDF）からアーカイブ。2008年8月16日閲覧。
8. "Google ディスカッシーグルーペン" . 2014 年 2 月 5 日に取得。
9. Weisstein, Eric W.「ロブスターグラフ」. MathWorld . 2025年9月5日閲覧。
10. ワイスタイン、エリック W.「ウェブグラフ」。マスワールド。