グラフ力学システム

数学において、グラフ動的システムの概念は、グラフやネットワーク上で起こる幅広いプロセスを捉えるために用いられます。グラフ動的システム（GDS）の数学的・計算的解析における主要なテーマは、その構造特性（例えば、ネットワークの接続性）と、それによって生じるグローバルダイナミクスを関連付けることです。

GDSに関する研究では、有限グラフと有限状態空間が対象とされます。そのため、研究には微分幾何学ではなく、グラフ理論、組合せ論、代数学、力学系などの手法が一般的に用いられます。原理的には、無限グラフ上のGDS（例えば、セルオートマトン、あるいはランダム性が含まれる相互作用粒子系上の確率的セルオートマトン）や、無限状態空間を持つGDS（例えば、結合写像格子など）を定義し、研究することができます。Wu [1] を参照。以下では、特に断りのない限り、すべては暗黙的に有限であると仮定します。 Z け {\displaystyle \mathbb {Z} ^{k}} R {\displaystyle \mathbb {R} }

正式な定義

グラフ動的システムは、次のコンポーネントから構成されます。

  • 頂点集合 v[ Y ] = {1,2, ... , n} を持つ有限グラフ Y。コンテキストに応じて、グラフは有向グラフまたは無向グラフとなる。
  • Yの各頂点vの状態x vは有限集合Kから得られる。システム状態はn次元の組x = ( x 1 , x 2 , ... , x n )であり、x [ v ] はYにおけるvの 1 近傍の頂点に関連付けられた状態を（ある固定順序で）組として表す。
  • 各頂点vに対する頂点関数 f v。頂点関数は、Yにおけるv の1近傍に関連付けられた状態に基づいて、時刻tにおける頂点vの状態を時刻t + 1における頂点状態にマッピングします。
  • 個々の頂点状態のマッピングが実行され、マップF : K n → K nを持つ離散動的システムが誘導されるメカニズムを指定する更新スキーム。

写像F : K n → K nを持つ力学系に付随する位相空間は、頂点集合K nと有向辺 ( x , F ( x ) )を持つ有限有向グラフである。位相空間の構造は、グラフY、頂点関数 ( f i ) i、および更新スキームの特性によって決まる。この分野の研究は、システム構成要素の構造に基づいて位相空間の特性を推論することを目指している。この解析は局所的から大域的に至る性質を持つ。

一般化セルオートマトン（GCA）

例えば、更新スキームが頂点関数を同期的に適用することから構成される場合、一般化セルオートマトン（CA）のクラスが得られる。この場合、全体写像F : K n → K nは次のように与えられる。

F （ × ） v ＝ f v （ × [ v ] ） 。 {\displaystyle F(x)_{v}=f_{v}(x[v])\;.}

このクラスは、古典的または標準的なセルラーオートマトンが通常、規則的なグラフまたはグリッド上で定義および研究され、頂点関数が通常同一であると想定されるため、一般化セルラーオートマトンと呼ばれます。

例: Y を頂点 {1,2,3,4} と辺 {1,2}、{2,3}、{3,4}、{1,4} を持つ円グラフとし、Circ 4 と表記します。各頂点の状態空間をK = {0,1} とし、すべての頂点関数に対して 2を法とする算術でnor 3 ( x,y,z ) = (1 +  x )(1 +  y )(1 +  z ) によって定義される関数 nor 3  : K 3 → Kを使用します。すると、例えばシステム状態 (0,1,0,0) は同期更新を使用して (0, 0, 0, 1) にマッピングされます。すべての遷移は、以下の位相空間に表示されます。

326

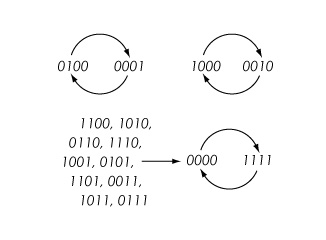
シーケンシャルダイナミックシステム（SDS）

頂点関数が、ワードw = ( w 1 , w 2 , ... , w m )またはv [ Y ]の順列= ( , )で指定されたシーケンスで非同期的に適用されると、シーケンシャル動的システム（SDS）のクラスが得られます。[2]この場合、頂点関数から構築された Y局所マップFiを導入すると便利です。 π {\displaystyle \pi } π 1 {\displaystyle \pi _{1}} π 2 、 … 、 π n {\displaystyle \pi _{2},\dots ,\pi _{n}}

F 私 （ × ） ＝ （ × 1 、 × 2 、 … 、 × 私 − 1 、 f 私 （ × [ 私 ] ） 、 × 私 + 1 、 … 、 × n ） 。 {\displaystyle F_{i}(x)=(x_{1},x_{2},\ldots ,x_{i-1},f_{i}(x[i]),x_{i+1},\ldots ,x_{n})\;.}

SDS写像F = [ F Y , w ] : K n → K nは関数合成である。

[ F はい 、 わ ] ＝ F わ （ メートル ） ∘ F わ （ メートル − 1 ） ∘ ⋯ ∘ F わ （ 2 ） ∘ F わ （ 1 ） 。 {\displaystyle [F_{Y},w]=F_{w(m)}\circ F_{w(m-1)}\circ \cdots \circ F_{w(2)}\circ F_{w(1)}\;.}

更新シーケンスが順列である場合、この点を強調するために 順列 SDSと呼ばれることがよくあります。

例: Y を頂点 {1,2,3,4} と辺 {1,2}、{2,3}、{3,4}、{1,4} を持つ円グラフとし、Circ 4 と表記します。各頂点の状態空間をK ={0,1} とし、すべての頂点関数に対して 2 を法とする算術でnor 3 ( x, y, z ) = (1 +  x )(1 +  y )(1 +  z ) で定義される関数nor 3  : K 3 → K を使用します。更新シーケンス (1,2,3,4) を使用すると、システム状態 (0, 1, 0, 0) は (0, 0, 1, 0) にマッピングされます。このシーケンシャルな動的システムのすべてのシステム状態遷移は、以下の位相空間に表示されます。

326

確率的グラフ力学システム

例えば、応用の観点から、GDSの構成要素の1つ以上に確率的要素が含まれるケースを検討することは興味深い。動機となる応用例としては、完全には理解されていないプロセス（例えば細胞内のダイナミクス）や、実用上、特定の側面が何らかの確率分布に従って振舞うように見えるケースなどが考えられる。また、決定論的な原理に支配され、その記述が非常に複雑または扱いにくいため、確率的近似を考慮することが理にかなっている応用もある。

グラフ力学系の各要素は、いくつかの方法で確率的に表現できます。例えば、シーケンシャル力学系では、更新シーケンスを確率的に表現できます。各反復ステップにおいて、対応する確率を持つ更新シーケンスの分布から、更新シーケンスwをランダムに選択できます。更新シーケンスの対​​応する確率空間は、SDSマップの確率空間を誘導します。この点に関して研究する自然な対象は、このSDSマップの集合によって誘導される状態空間上のマルコフ連鎖です。このケースは更新シーケンス確率的GDSと呼ばれ、例えば、一定の速度に従ってランダムに「イベント」が発生するプロセス（例えば化学反応）、並列計算／離散イベントシミュレーションにおける同期、そして後述する計算パラダイムなどがその例です。

確率的更新シーケンスを用いたこの具体的な例は、このようなシステムに関する2つの一般的な事実を示しています。確率的グラフ力学システムに移行すると、一般的に(1)マルコフ連鎖（GDSの構成要素によって支配される特定の構造を持つ）の研究へと導かれ、(2)結果として得られるマルコフ連鎖は指数関数的な状態数を持つ大規模なものになる傾向があります。確率的GDS研究の中心的な目標は、縮約モデルを導出できるようにすることです。

頂点関数が確率的である場合、すなわち関数確率GDS（function stochastic GDS）も考えられます。例えば、ランダムブールネットワークは、同期更新方式を用い、状態空間がK = {0, 1}である関数確率GDSの例です。有限確率セルオートマトン（PCA）も関数確率GDSの例です。原理的には、相互作用粒子システム（IPS）のクラスは有限および無限PCAをカバーしますが、実際にはIPSの研究は主に無限の場合を対象としています。これは、無限の場合の方が状態空間上により興味深いトポロジーを導入できるためです。

アプリケーション

グラフ動的システムは、生物学的ネットワークやソーシャル ネットワーク上の伝染病などの分散システムを捕捉するための自然なフレームワークを構成し、その多くは複雑システムと呼ばれることがよくあります。

参照

参考文献

  1. ^ Wu, Chai Wah (2005). 「有向グラフを介して結合された非線形動的システムネットワークにおける同期」.非線形性. 18 (3): 1057– 1064. Bibcode :2005Nonli..18.1057W. doi :10.1088/0951-7715/18/3/007. S2CID  122111995.
  2. ^ Mortveit, Henning S.; Reidys, Christian M. (2008).シーケンシャル動的システム入門. Universitext. ニューヨーク: Springer Verlag . ISBN 978-0-387-30654-4。

さらに読む

  • マコーリー, マシュー; モルトベイト, ヘニング S. (2009). 「グラフ動的システムのサイクル同値性」.非線形性. 22 (2): 421– 436. arXiv : 0802.4412 . Bibcode :2009Nonli..22..421M. doi :10.1088/0951-7715/22/2/010. S2CID  17978550.
  • ゴルビツキー、マーティン、スチュワート、イアン (2003). 『対称性の視点』 バーゼル：ビルクハウザー. ISBN 0-8176-2171-7。
  • グラフ動的システム - 相互作用ベースシステム、その分析およびシミュレーションのための数学的枠組み（ヘニング・モルトベイト著）
Retrieved from "https://en.wikipedia.org/w/index.php?title=Graph_dynamical_system&oldid=1265271544"