七面体

7つの面を持つ多面体

正三角形4つと凧形3つの面で構成された正三角形で、面積はすべて同じである。^[1]

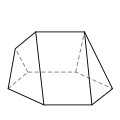
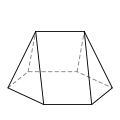
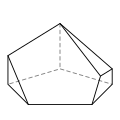
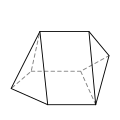
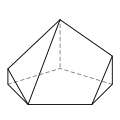
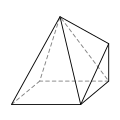
七面体（複数形：heptahedra）は、7 つの辺または面を持つ多面体です。

七面体は、多様な基本形状、すなわち位相をとることができます。最もよく知られているのは、六角錐と五角柱です。また、実射影平面のモザイク状と見ることができる四半六面体も注目に値します。どの七面体も正六面体ではありません。

位相的に異なる七面体

凸型

位相的に異なる凸七面体は、鏡像を除いて34個あります。 ^[2]（2つの多面体は、面と頂点の配置が本質的に異なり、単に辺の長さや辺または面の間の角度を変えるだけでは、一方を他方に歪ませることができない場合、「位相的に異なる」多面体です。）

以下に、各タイプの例と、それぞれの面の辺の数を示します。画像は、6辺面（ある場合）の数が多い順に並べられており、続いて5辺面（ある場合）の数が多い順に並べられています。

面: 6,6,4,4,4,3,3 10頂点 15エッジ	面: 6,5,5,5,3,3,3 10頂点 15エッジ	面: 6,5,5,4,4,3,3 10頂点 15エッジ	面: 6,5,4,4,3,3,3 9つの頂点 14エッジ	面: 6,5,4,4,3,3,3 9つの頂点 14エッジ
面: 6,4,4,4,4,3,3 9つの頂点 14エッジ	面: 6,4,4,3,3,3,3 8つの頂点 13エッジ	面: 6,4,4,3,3,3,3 8つの頂点 13エッジ	六角錐面: 6,3,3,3,3,3,3,3 7つの頂点 12エッジ	面: 5,5,5,4,4,4,3 10頂点 15エッジ
面: 5,5,5,4,3,3,3 9つの頂点 14エッジ	面: 5,5,5,4,3,3,3 9つの頂点 14エッジ	五角柱面: 5,5,4,4,4,4,4 10頂点 15エッジ	面: 5,5,4,4,4,3,3 9つの頂点 14エッジ	面: 5,5,4,4,4,3,3 9つの頂点 14エッジ
面: 5,5,4,3,3,3,3 8つの頂点 13エッジ	面: 5,5,4,3,3,3,3 8つの頂点 13エッジ	面: 5,4,4,4,4,4,4,3 9つの頂点 14エッジ	面: 5,4,4,4,3,3,3 8つの頂点 13エッジ	面: 5,4,4,4,3,3,3 8つの頂点 13エッジ
面: 5,4,4,4,3,3,3 8つの頂点 13エッジ	面: 5,4,4,4,3,3,3 8つの頂点 13エッジ	面: 5,4,4,4,3,3,3 8つの頂点 13エッジ	面: 5,4,3,3,3,3,3,3 7つの頂点 12エッジ	面: 5,4,3,3,3,3,3,3 7つの頂点 12エッジ
面: 4,4,4,4,4,3,3 8つの頂点 13エッジ	面: 4,4,4,4,4,3,3 8つの頂点 13エッジ	細長い三角錐面: 4,4,4,3,3,3,3 7つの頂点 12エッジ	面: 4,4,4,3,3,3,3 7つの頂点 12エッジ	面: 4,4,4,3,3,3,3 7つの頂点 12エッジ
縮小立方体面: 4,4,4,3,3,3,3 7つの頂点 12エッジ	面: 4,4,4,3,3,3,3 7つの頂点 12エッジ	面: 4,3,3,3,3,3,3,3 6つの頂点 11 エッジ	面: 4,3,3,3,3,3,3,3 6つの頂点 11 エッジ

凹面

2つの四面体を様々な配置で組み合わせることで、位相的に異なる6つの凹七面体（鏡像を除く）を形成できます。これらのうち3番目、4番目、5番目の面は、隣接する辺が同一線上にある面を持ち、6番目の面は単連結ではありません。^[要出典]
三角柱または四角錐の辺に切り込みを入れることで、位相的に異なる13個の七面体（鏡像を除く）を形成できます。2つの例を示します。	単純連結でない七面体には様々な種類があります。2つの例を示します。^[要出典]