水平線テスト

数学において、水平線テストは関数が単射（つまり1対1）であるかどうかを判断するために使用されるテストです。 ^[1]

微積分学では

水平線とは、左から右へ伸びる直線のことです。関数（つまり、実数から実数への関数）が与えられた場合、関数のグラフと交差する水平線を見ることで、その関数が単射かどうかを判断できます。水平線 がグラフと複数の点で交差する場合、その関数は単射ではありません。これを確認するには、交点のy値は同じ（直線上にあるため）ですが、x値は異なることに注意してください。これは定義上、関数が単射ではないことを意味します。^[1]${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$ ${\displaystyle y=c}$ ${\displaystyle y=c}$

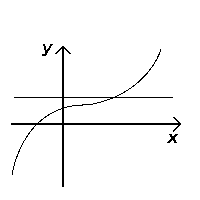テストに合格する（単射）

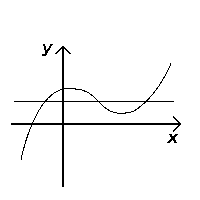テストに不合格（単射ではない）

水平線テストのバリエーションは、関数が全射か全単射かを判断するために使用できます。

• 関数fは、そのグラフが任意の水平線と少なくとも1回交差する場合に限り、射影的 (つまり全射) になります。
• fは、任意の水平線がグラフと正確に1 回交差する場合に限り、全単射です。

集合論では

対応するグラフが直積の部分集合である関数を考えます。関数fが単射となるのは 、各水平線がグラフと最大1回交差する場合のみです。この場合、グラフは水平線テストに合格すると言えます。水平線がグラフと2回以上交差する場合、関数は水平線テストに合格せず、単射ではありません。^[2]${\displaystyle f\colon X\to Y}$ ${\displaystyle X\times Y}$ ${\displaystyle X\times Y}$ ${\displaystyle \{(x,y_{0})\in X\times Y:y_{0}{\text{ は定数}}\}=X\times \{y_{0}\}}$

参照

• 垂直線テスト
• 逆関数
• 単調関数

参考文献

1. スチュワート、ジェームズ(2003). 『一変数微積分学：初期超越関数』（第5版）トロント ON: Brook/Cole. pp. 64. ISBN 0-534-39330-6. 2012年7月15日閲覧。したがって、関数が1対1であるかどうかを判断するための幾何学的手法は次のようになります。
2. ゾーン、ポール、オステビー、アーノルド (2002). グラフ、数値、記号の観点から見た微積分学（第2版）. オーストラリア: Brooks/Cole/Thomson Learning. p. 185. ISBN 0-03-025681-X水平線が f グラフを複数回横切ることはありません。