ヒューズ・ドレーバー実験
D 2 O中の LiCl (1M) の7 Li NMR スペクトル。このリチウム同位体の鋭く分裂していない NMR 線は、質量と空間の等方性の証拠です。

ヒューズ・ドレーバー実験（時計比較実験、時計異方性実験、質量等方性実験、エネルギー等方性実験とも呼ばれる）は、質量と空間の等方性を分光学的に検証する実験である。当初はマッハの原理を検証するものとして考え出されたが、現在ではローレンツ不変性を検証する重要なテストであると理解されている。マイケルソン・モーリー実験と同様に、好ましい参照系の存在やローレンツ不変性からのその他の逸脱を検証することができ、これは等価性原理の妥当性にも影響する。したがって、これらの実験は特殊相対性理論と一般相対性理論の両方の基本的な側面に関係している。マイケルソン・モーリー型の実験と異なり、ヒューズ・ドレーバー実験では物質自体、つまり陽子、中性子、電子の相互作用の等方性を検証する。達成された精度により、この種の実験は相対性理論の最も正確な確認の一つとなっている（特殊相対性理論の検証も参照）。[ 1 ] [ 2 ] [ 3 ] [ 4 ] [ 5 ] [ 6 ]

ヒューズとドレバーによる実験

ジュゼッペ・コッコーニとエドウィン・アーネスト・サルペター（1958）は、マッハの原理に従って、慣性は周囲の質量に依存すると理論化した。したがって、物質の不均一な分布は、異なる方向に慣性の異方性をもたらす。経験的な議論から、彼らは、もし慣性異方性が存在するならば、それは我々の天の川銀河の中心からの質量寄与によって支配されるだろうと信じるに至った。彼らは、この異方性は、原子のゼーマン分裂を測定すること[ 7 ] 、または励起原子核状態のゼーマン分裂を測定することの2つの方法で観測できると主張した。57メスバウアー効果を利用したFe。 [ 8 ]

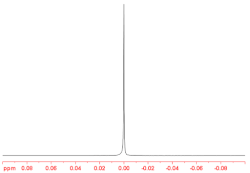
Vernon W. Hughesら(1960) [ 9 ]とRonald Drever (1961) [ 10 ]はそれぞれ独立に同様の分光実験を行い、マッハの原理を検証しました。しかし、メスバウアー効果は使用せず、基底状態でスピン3 ⁄ 2を持つリチウム-7の原子核の磁気共鳴測定を行いました。基底状態は、許容される磁気量子数に従って磁場中で測定すると、4 つの等間隔の磁気エネルギー準位に分割されます。異なるエネルギー準位の原子核波動関数は、磁場に対して異なる空間分布を持ち、したがって異なる方向性を持ちます。質量等方性が満たされる場合、一対の隣接する準位間の各遷移で等しい周波数の光子が放出され、単一の鋭いスペクトル線が生じます。一方、慣性に方向依存性がある場合は、三重項または広がった共鳴線が観測されるはずです。ドレーヴァー版の実験では、24時間にわたって地球が回転し、磁場の軸が空のさまざまな部分を横切りました。ドレーヴァーは、磁場が銀河の中心を横切る際のスペクトル線の挙動に特に注目しました。[ 11 ]ヒューズもドレーヴァーもエネルギー準位の周波数シフトを観測しておらず、実験の高精度化により、最大異方性は0.04  Hz = 10 −25 GeVに制限されました。  

マッハの原理の帰結に関して、ロバート・H・ディッケ（1961）は、空間異方性がすべての粒子に対して同一である限り、マッハの原理と一致することを示した。したがって、この帰結はむしろ、慣性異方性効果が存在する場合、それがすべての粒子に対して普遍的であり、局所的には観測不可能であることを示している。[ 12 ] [ 13 ]

現代的な解釈

この実験の動機はマッハの原理をテストすることであったが、それ以来、ローレンツ不変性、ひいては特殊相対性理論の重要なテストとして認識されるようになった。これは、異方性効果が、ローレンツ不変性を破る優先参照系（通常は、ある種の光伝導エーテル（相対速度約368 km/s）としてCMBR静止系と同一視される）の存在下でも発生するためである。したがって、ヒューズ–ドレーバー実験（およびマイケルソン–モーリー実験）の否定的な結果は、そのような系の存在を排除する。特に、ローレンツ非保存のヒューズ–ドレーバーテストは、クリフォード・ウィルが提唱した特殊相対性理論のテスト理論によって説明されることが多い。このモデルによると、優先参照系の存在下でのローレンツ非保存は、質量の大きい粒子の最大到達速度と光速との間に差をもたらす可能性がある。もしこれらが異なれば、物質相互作用の特性と頻度も変化するであろう。さらに、一般相対性理論の等価原理の基本的な帰結として、自由に移動する基準系においてローレンツ不変性が局所的に成立すること（局所ローレンツ不変性、LLI）が挙げられます。これは、この実験結果が特殊相対性理論と一般相対性理論の両方に関係していることを意味します。[ 1 ] [ 2 ]

異なる周波数（「クロック」）を比較するため、これらの実験はクロック比較実験とも呼ばれます。[ 3 ] [ 4 ]

最近の実験

マッハの原理に基づく優先座標系や影響によるローレンツ対称性の破れに加え、様々な量子重力モデルがそれらの存在を示唆する予測に基づき、ローレンツ不変性とCPT対称性の自発的な破れも探索されている。ヒューズ・ドレーバー実験の最新版では、中性子と陽子におけるローレンツ対称性とCPT対称性の破れの可能性を研究している。スピン偏極システムと共磁力計（磁気の影響を抑制するため）を用いることで、これらの実験の精度と感度は大幅に向上した。さらに、スピン偏極トーションバランスを用いることで、電子セクターも試験されている。[ 5 ] [ 6 ]

これらの実験はすべてこれまでのところ否定的な結果を示しており、優先座標系の存在やその他の形態のローレンツ不変性の兆候はまだ見られません。以下の表の値は、ローレンツ不変性の破れの可能性を評価するためによく用いられる有効場理論である標準模型拡張（SME）によって与えられた係数と関連しています（特殊相対論の他のテスト理論も参照）。これにより、ローレンツ不変性のあらゆる逸脱は特定の係数と関連付けることができます。これらの実験では一連の係数がテストされているため、最大感度の値のみが示されています（正確なデータについては、個々の論文を参照してください）。[ 3 ] [ 14 ] [ 4 ]

著者 年 中小企業の制約 説明
プロトン中性子電子
プレステージら[ 15 ]198510 −27核スピン反転遷移を比較すると9なれ+（ペニングトラップに保存）水素メーザー遷移を伴います。
フィリップス[ 16 ]198710 −27横方向に分極した磁石を搭載した 極低温スピンねじり振り子を使用して正弦波振動を調査しました。
ラモローら[ 17 ]198910 −29彼らは、蒸気に双極子と四極子スピン分極を誘導した。201Hg、これにより四重極エネルギーシフトを観測することができます。
チャップら[ 18 ]198910 −27ゼーマン準位の時間依存四重極分裂を調査します。21ネと3Heガスはスピン交換によって分極され、比較されます。
ワインランドら[ 19 ]199110 −25異常な双極子-単極子結合と双極子-双極子結合は、超微細共鳴を調べることによって調査される。9なれ+。
王ら[ 20 ]199310 −27スピン偏極したDy – Fe質量を持つスピンねじり振り子の恒星変化が調査されます。
ベルグランドら[ 21 ]199510 −2710 −3010 −27磁場を印加して 199 Hgと133 Csの周波数を比較します。
ベアら[ 22 ]​200010 −31の周波数129Xeと3ゼーマンメーザーを比較します。
フィリップスら[ 23 ]200010 −27ゼーマン周波数は水素メーザーを使用して測定されます。
ハンフリーら[ 24 ]200310 −2710 −27Phillips et al. (2000) と同様。
Houら[ 14 ]200310 −29Wang et al. (1993) と同様。
カネら[ 25 ]​200410 −32Bear et al. (2000) と同様。
ウルフら[ 26 ]200610 −25原子周波数はレーザー冷却法で測定される133Cs原子泉。
ヘッケルら[ 27 ]200610 −30彼らは、4 つのセクションのアルニコと 4 つのセクションのSm 5 Coを備えたスピン トーション 振り子を使用しました。
ヘッケルら[ 28 ]200810 −31Heckel らと同様。 （2006年）。
アルタレフら[ 29 ]200910 −29貯蔵された超冷中性子と199Hgが分析されます。
ブラウンら[ 30 ]201010 −3210 −33K /の頻度を比較する3彼は 磁力計です。
ゲンメルら[ 31 ]201010 −32周波数を比較すると129キセ/3彼は磁力計です。
スミチクラスら[ 32 ]201110 −29周波数を比較すると21Ne / Rb / K共磁力計。中性子の最大到達速度の試験。
ペックら[ 33 ]201210 −3010 −31Berglund et al. (1995) と同様。
ホーエンゼーら[ 34 ]201310 −17二つのほぼ縮退した状態の遷移周波数を測定する164Dyと162Dy。電子の最大到達速度のテスト。
アルメンディンガーら[ 35 ]201310 −34Gemmel et al. (2010) と同様。

参考文献

  1. ^ a b Will, CM (2006). 「一般相対性理論と実験の対立」 . Living Reviews in Relativity . 9 (3): 3. arXiv : gr-qc/0510072 . Bibcode : 2006LRR.....9....3W . doi : 10.12942 /lrr-2006-3 . PMC  5256066. PMID 28179873  .
  2. ^ a b Will, CM (1995). 「安定時計と一般相対性理論」. Proceedings of the 30th Rencontres de Moriond : 417. arXiv : gr-qc/9504017 . Bibcode : 1995dmcc.conf..417W .
  3. ^ a b c Kostelecký, V. Alan; Lane, Charles D. (1999). 「クロック比較実験によるローレンツ対称性の破れに対する制約」. Physical Review D. 60 ( 11) 116010. arXiv : hep-ph/9908504 . Bibcode : 1999PhRvD..60k6010K . doi : 10.1103/PhysRevD.60.116010 . S2CID 119039071 . 
  4. ^ a b c Mattingly, David (2005). 「ローレンツ不変性の現代的検定」 . Living Rev. Relativ . 8 (5): 5. arXiv : gr-qc/0502097 . Bibcode : 2005LRR.....8....5M . doi : 10.12942 / lrr-2005-5 . PMC 5253993. PMID 28163649 .  
  5. ^ a b Pospelov, Maxim; Romalis, Michael (2004). "Lorentz Invariance on Trial" (PDF) . Physics Today . 57 (7): 40– 46. Bibcode : 2004PhT....57g..40P . doi : 10.1063/1.1784301 .オリジナル(PDF)から2022年1月2日にアーカイブ。 2011年5月26日閲覧。
  6. ^ a b Walsworth, RL (2006). 「スピン結合セクターにおけるローレンツ対称性のテスト」(PDF) .特殊相対論. 物理学講義ノート. 第702巻. pp.  493– 505. doi : 10.1007/3-540-34523-X_18 . ISBN 978-3-540-34522-0。
  7. ^コッコーニ、G.サルピーター E. (1958)。 「慣性の異方性の探索」。イル・ヌオーヴォ・シメント。10 (4): 646–651。Bibcode : 1958NCim...10..646C。土井：10.1007/BF02859800。S2CID 123226805。 
  8. ^ Cocconi, G.; Salpeter E. (1960). 「メスバウアー効果による慣性異方性の上限」. Physical Review Letters . 4 (4): 176– 177. Bibcode : 1960PhRvL...4..176C . doi : 10.1103/PhysRevLett.4.176 .
  9. ^ Hughes, VW; Robinson, HG; Beltran-Lopez, V. (1960). 「核共鳴実験による慣性質量の異方性の上限」. Physical Review Letters . 4 (7): 342– 344. Bibcode : 1960PhRvL...4..342H . doi : 10.1103/PhysRevLett.4.342 .
  10. ^ Drever, RWP (1961). 「自由歳差運動法を用いた慣性質量の異方性の探索」. Philosophical Magazine . 6 (65): 683– 687. Bibcode : 1961PMag....6..683D . doi : 10.1080/14786436108244418 .
  11. ^バルトゥシアク、マーシャ（2003年）『アインシュタインの未完成交響曲：時空の音に耳を傾ける』ジョセフ・ヘンリー・プレス、  96～ 97頁。ISBN 0-425-18620-2. 2012年7月15日閲覧。「地球が自転する24時間にわたって、その線を観察しました。磁場の軸が銀河の中心を過ぎたり、他の方向に動いたりするたびに、変化を探しました」とドレバーは回想する。
  12. ^ Dicke, RH (1961). 「マッハの原理の実験的検証」. Physical Review Letters . 7 (9): 359– 360. Bibcode : 1961PhRvL...7..359D . doi : 10.1103/PhysRevLett.7.359 .
  13. ^ディッケ, RH (1964).実験相対論の理論的意義. ゴードンとブリーチ.
  14. ^ a b Hou, Li-Shing; Ni, Wei-Tou; Li, Yu-Chu M. (2003). 「回転式ねじり天秤を用いた偏極電子の宇宙空間等方性の検証」. Physical Review Letters . 90 (20) 201101. arXiv : physics/0009012 . Bibcode : 2003PhRvL..90t1101H . doi : 10.1103/PhysRevLett.90.201101 . PMID 12785879. S2CID 28211115 .  
  15. ^ Prestage, JD; Bollinger, JJ; Itano, WM; Wineland, DJ (1985). 「核スピン偏極Be-9(+)イオンを用いた空間異方性の限界」. Physical Review Letters . 54 (22): 2387– 2390. Bibcode : 1985PhRvL..54.2387P . doi : 10.1103/PhysRevLett.54.2387 . PMID 10031329 . 
  16. ^ Phillips, PR (1987). 「極低温スピンねじり振り子を用いた空間等方性の検証」. Physical Review Letters . 59 (5): 1784– 1787. Bibcode : 1987PhRvL..59.1784P . doi : 10.1103/PhysRevLett.59.1784 . PMID 10035328 . 
  17. ^ Lamoreaux, SK; Jacobs, JP; Heckel, BR; Raab, FJ; Fortson, EN (1989). 「1S(0)原子における小さな核四重極シフトの測定と空間等方性の試験のための光ポンピング技術」. Physical Review A. 39 ( 3): 1082– 1111. Bibcode : 1989PhRvA..39.1082L . doi : 10.1103/PhysRevA.39.1082 . PMID 9901347 . 
  18. ^ Chupp, TE; Hoare, RJ; Loveman, RA; Oteiza, ER; Richardson, JM; Wagshul, ME; Thompson, AK (1989). 「局所ローレンツ不変性の新たな検証結果：21Neにおける質量異方性の探索」. Physical Review Letters . 63 (15): 1541– 1545. Bibcode : 1989PhRvL..63.1541C . doi : 10.1103/PhysRevLett.63.1541 . PMID 10040606 . 
  19. ^ Wineland, DJ; Bollinger, JJ; Heinzen, DJ; Itano, WM; Raizen, MG (1991). 「蓄積イオン分光法を用いた異常スピン依存力の探索」. Physical Review Letters . 67 (13): 1735– 1738. Bibcode : 1991PhRvL..67.1735W . doi : 10.1103/PhysRevLett.67.1735 . PMID 10044234 . 
  20. ^ Wang, Shih-Liang; Ni, Wei-Tou; Pan, Sheau-Shi (1993). 「分極電子の空間異方性に関する新たな実験的限界」. Modern Physics Letters A. 8 ( 39): 3715– 3725. Bibcode : 1993MPLA....8.3715W . doi : 10.1142/S0217732393003445 .
  21. ^ Berglund, CJ; Hunter, LR; Krause, D. Jr.; Prigge, EO; Ronfeldt, MS; Lamoreaux, SK (1995). 「水銀およびセシウム磁力計による局所ローレンツ不変性の新たな限界」. Physical Review Letters . 75 (10): 1879– 1882. Bibcode : 1995PhRvL..75.1879B . doi : 10.1103/PhysRevLett.75.1879 . PMID 10059152 . 
  22. ^ Bear, D.; Stoner, RE; Walsworth, RL; Kostelecký, V. Alan; Lane, Charles D. (2000). 「2種希ガスメーザーを用いた中性子のローレンツ限界とCPT破れの限界」. Physical Review Letters . 85 (24): 5038– 5041. arXiv : physics/0007049 . Bibcode : 2000PhRvL..85.5038B . doi : 10.1103/ PhysRevLett.85.5038 . PMID 11102181. S2CID 41363493 .  
  23. ^ Phillips, DF; Humphrey, MA; Mattison, EM; Stoner, RE; Vessot, RF; Walsworth, RL (2001). 「水素メーザーを用いた陽子のローレンツ限界とCPT破れの限界」. Physical Review D. 63 ( 11) 111101. arXiv : physics/0008230 . Bibcode : 2001PhRvD..63k1101P . doi : 10.1103/PhysRevD.63.111101 . S2CID 10665017 . 
  24. ^ Humphrey, MA; Phillips, DF; Mattison, EM; Vessot, RF; Stoner, RE; Walsworth, RL (2003). 「水素メーザーによるCPTおよびローレンツ対称性の検証」. Physical Review A. 68 ( 6) 063807. arXiv : physics/0103068 . Bibcode : 2003PhRvA..68f3807H . doi : 10.1103/PhysRevA.68.063807 . S2CID 13659676 . 
  25. ^ Canè, F.; Bear, D.; Phillips, DF; Rosen, MS; Smallwood, CL; Stoner, RE; Walsworth, RL; Kostelecký, V. Alan (2004). 「中性子に対するローレンツ境界およびCPT非保存ブースト効果」. Physical Review Letters . 93 (23) 230801. arXiv : physics/0309070 . Bibcode : 2004PhRvL..93w0801C . doi : 10.1103/PhysRevLett.93.230801 . PMID 15601138. S2CID 20974775 .  
  26. ^ Wolf, P.; Chapelet, F.; Bize, S.; Clairon, A. (2006). 「Cold Atom Clock Test of Lorentz Invariance in the Matter Sector」. Physical Review Letters . 96 (6) 060801. arXiv : hep-ph/0601024 . Bibcode : 2006PhRvL..96f0801W . doi : 10.1103/PhysRevLett.96.060801 . PMID 16605978. S2CID 141060 .  
  27. ^ Heckel, BR; Cramer, CE; Cook, TS; Adelberger, EG; Schlamminger, S.; Schmidt, U. (2006). 「分極電子を用いた新しいCP対称性の破れと優先座標系のテスト」. Physical Review Letters . 97 (2) 021603. arXiv : hep-ph/0606218 . Bibcode : 2006PhRvL..97b1603H . doi : 10.1103/ PhysRevLett.97.021603 . PMID 16907432. S2CID 27027816 .  
  28. ^ Heckel, BR; Adelberger, EG; Cramer, CE; Cook, TS; Schlamminger, S.; Schmidt, U. (2008). 「偏極電子を用いた優先フレームとCP対称性の破れのテスト」. Physical Review D. 78 ( 9) 092006. arXiv : 0808.2673 . Bibcode : 2008PhRvD..78i2006H . doi : 10.1103/PhysRevD.78.092006 . S2CID 119259958 . 
  29. ^ Altarev, I.; et al. (2009). 「超冷中性子のスピン歳差運動によるローレンツ不変性の検証」. Physical Review Letters . 103 (8) 081602. arXiv : 0905.3221 . Bibcode : 2009PhRvL.103h1602A . doi : 10.1103/PhysRevLett.103.081602 . PMID 19792714. S2CID 5224718 .  
  30. ^ Brown, JM; Smullin, SJ; Kornack, TW; Romalis, MV (2010). 「ローレンツおよびCPTを破る中性子スピン相互作用に関する新たな限界」. Physical Review Letters . 105 (15) 151604. arXiv : 1006.5425 . Bibcode : 2010PhRvL.105o1604B . doi : 10.1103/PhysRevLett.105.151604 . PMID 21230893. S2CID 4187692 .  
  31. ^ Gemmel, C.; Heil, W.; Karpuk, S.; Lenz, K.; Sobolev, Yu.; Tullney, K.; Burghoff, M.; Kilian, W.; Knappe-Grüneberg, S.; Müller, W.; Schnabel, A.; Seifert, F.; Trahms, L.; Schmidt, U. (2010). 「自由歳差運動He3/Xe129共磁力計を用いた束縛中性子のローレンツ限界およびCPT破れの限界」. Physical Review D. 82 ( 11) 111901. arXiv : 1011.2143 . Bibcode : 2010PhRvD..82k1901G . doi : 10.1103/PhysRevD.82.111901 . S2CID 118438569。 
  32. ^ M. Smiciklas; et al. (2011). 「21Ne-Rb-K共磁力計を用いた局所ローレンツ不変性の新たな検証」. Physical Review Letters . 107 (17) 171604. arXiv : 1106.0738 . Bibcode : 2011PhRvL.107q1604S . doi : 10.1103/PhysRevLett.107.171604 . PMID 22107506. S2CID 17459575 .  
  33. ^ Peck, SK; et al. (2012). 「水銀とセシウムにおける局所ローレンツ不変性の新たな限界」. Physical Review A. 86 ( 1) 012109. arXiv : 1205.5022 . Bibcode : 2012PhRvA..86a2109P . doi : 10.1103/PhysRevA.86.012109 . S2CID 118619087 . 
  34. ^ Hohensee, MA; et al. (2013). 「原子ジスプロシウムの無線周波数分光法を用いたローレンツ対称性とアインシュタイン等価原理の破れの限界」. Physical Review Letters . 111 (5) 050401. arXiv : 1303.2747 . Bibcode : 2013PhRvL.111e0401H . doi : 10.1103/PhysRevLett.111.050401 . PMID 23952369. S2CID 27090952 .  
  35. ^ Allmendinger, F.; et al. (2014). 「自由歳差運動型He-Xe共磁力計を用いたローレンツおよびCPT非保存中性子スピン相互作用に関する新たな限界」. Physical Review Letters . 112 (11) 110801. arXiv : 1312.3225 . Bibcode : 2014PhRvL.112k0801A . doi : 10.1103/PhysRevLett.112.110801 . PMID 24702343. S2CID 8122573 .  
「 https://en.wikipedia.org/w/index.php?title=Hughes–Drever_experiment&oldid=1313897776」より取得