ファロシャッフル

完璧にインターリーブされたトランプシャッフル

ファロシャッフル（アメリカ式）、ウィーブシャッフル（イギリス式）、またはダブテイルシャッフルは、トランプのシャッフル方法の一種で、両手に山札の半分を持ち、親指を内側に向けます。そして、親指でカードを離し、カードを交互にテーブルに落とします。ディアコニス、グラハム、カンターは、マジックにおいてこの技法を「テクニック」と呼んでいます。 ^[1]

数学者は、1組のカードを26枚の等しい山に正確に並べ替え、それらを完璧に重ね合わせることを「ファロシャッフル」と呼びます。^[2]

説明

右利きの人は、左手で上から、右手で下からカードを持ちます。右手の親指でカードの半分を軽く持ち上げ、左手の束を右手から離すように前方に押し出すだけで、デッキは2つの均等な部分に分けられます。2つの束は交差させ、軽く叩いて位置を合わせます。次に、短い辺を押し合わせて上または下に折り曲げます。すると、カードは交互に重なり合い、理想的にはジッパーのように、半分から1枚ずつ交互に落ちます。上から圧力をかけて束を折り曲げることで、華やかさを加えることができます。^[3]

ファロのゲームは、ディーラーが次のゲームのためにカードを2つの同じ山に分けることで終了します。マジシャンのジョン・マスケリンによると、上記の方法が用いられ、彼はこれを「ファロディーラーのシャッフル」と呼んでいます。^{[4]マスケリンは明確な指示を与えた最初の人物ですが、シャッフルは以前からファロと関連付けられており、主に数学者でありマジシャンで}もあるペルシ・ディアコニスによって発見されました。^[5]

完璧なシャッフル

ファロシャッフルは、デッキを完全にランダム化しない制御されたシャッフルです。

カードが完全に交互になっている完璧なファロシャッフルを行うには、シャッフルする人がデッキを 2 つの均等なスタックに切り分け、ハーフデッキを互いに押し込むときに適切な圧力をかけることが必要です。

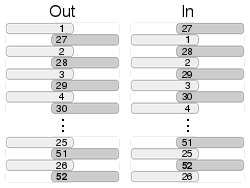
ファロシャッフルにおいて、元の一番上のカードを一番上に、元の一番下のカードを一番下に残すシャッフルはアウトシャッフルと呼ばれ、元の一番上のカードを二番目に、元の一番下のカードを二番目に移動するシャッフルはインシャッフルと呼ばれます。これらの名称は、マジシャンでありコンピュータプログラマーでもあるアレックス・エルムズリーによって考案されました。^[6]

アウトシャッフルは、一番上と一番下のカードを取り除いて残りのカードをインシャッフルし、一番上と一番下のカードを元の位置に戻すのと同じ結果になります。アウトシャッフルを繰り返してもデッキ全体の順序は逆転せず、中央のn−2枚のカードの順序のみが逆転します。ファロシャッフルに関する数学的定理は、アウトシャッフルに言及することが多い。

インシャッフルは、デッキの一番上に不要なカードを1枚、一番下に不要なカードを1枚追加し、デッキを拡大した状態でアウトシャッフルし、不要なカードを取り除くのと同じ結果になります。インシャッフルを繰り返すと、デッキの順序が逆になることがあります。

完璧なインシャッフルができれば、26回のシャッフルでデッキの順序が逆になり、さらに26回シャッフルすると元の順序に戻ります。^[7]

一般に、の場合、完璧なインシャッフルによって - 枚のカードのデッキの順序が復元されます。たとえば、の理由により、52 回連続してインシャッフルを行うと 52 枚のカードのデッキの順序が復元されます。 $k$ $n$ $2^{k}\equiv 1{\pmod {n+1}}$ $2^{52}\equiv 1{\pmod {53}}$

一般的に、の場合には、完璧なアウトシャッフルによって - 枚のカードのデッキの順序が復元されます。例えば、の場合には、8 回連続でアウトシャッフルを実行すると、の理由により、52 枚のカードのデッキは元の順序に戻ります。ただし、 64 枚のカードのデッキの順序を復元するには、6 回のファロアウトシャッフルのみが必要です。 $k$ $n$ $2^{k}\equiv 1{\pmod {n-1}}$ $2^{8}\equiv 1{\pmod {51}}$

言い換えると、偶数サイズnのカードのデッキを元の順序に戻すために必要なインシャッフルの数は、 2 を法とした( n + 1) の乗法順序で決まります。

たとえば、デッキサイズがn =2、4、6、8、10、12 ... の場合、必要なインシャッフルの数は、2、4、3、6、10、12、4、8、18、6、11、... です ( OEISのシーケンスA002326 )。

アルティンの原始根に関する予想によれば、 n回のシャッフルを必要とするデッキサイズは無限に存在することになる。^[8]

無限シーケンスのアウトシャッフルに類似した操作は、インターリーブシーケンスです。

例

簡単にするために、6 枚のカードのデッキを使用します。

以下は、インシャッフル後のデッキの順序を示しています。このサイズのデッキは、3回のインシャッフルで元の順序に戻ります。

ステップ	トップカード	2	3	4	5	一番下のカード
始める
1
2
3

以下は、アウトシャッフル後のデッキの順序を示しています。このサイズのデッキは、4回のアウトシャッフルで元の順序に戻ります。

ステップ	トップカード	2	3	4	5	一番下のカード
始める
1
2
3
4

デッキ操作として

マジシャンのアレックス・エルムズリーは、インシャッフルとアウトシャッフルを制御された順序で繰り返すことで、デッキの一番上のカードを任意の位置に移動できることを発見しました^{[要出典] 。このトリックは、カードの望ましい位置を}2進数で表し、1ごとにインシャッフル、0ごとにアウトシャッフルを行うというものです。

例えば、一番上のカードを下に動かして、その上に10枚のカードがある場合、10を2進数で表します（1010 ₂）。イン、アウト、イン、アウトとシャッフルします。デッキの上から10枚のカードを配り、11枚目が元のカードになります。10を1010 ₂と表しても、00001010 ₂と表しても問題ありません。予備的なアウトシャッフルは結果に影響を与えません。アウトシャッフルは常に一番上のカードを上にするためです。

群論の側面

数学では、完全なシャッフルは対称群の要素と考えることができます。

より一般的には、において、完全なシャッフルとは、セットを 2 つの山に分割し、それらを交互に配置する順列です。 $S_{2n}$

S_{2n}

＝

{\begin{pmatrix}1&2&3&4&\cdots &2n-1&2n\\1&n+1&2&n+2&\cdots &n&2n\end{pmatrix}}

つまり、それは地図です

k\mapsto {\begin{cases}{\frac {k+1}{2}}&k\ {\text{odd}}\\n+{\frac {k}{2}}&k\ {\text{even}}\end{cases}}

同様に、完全シャッフル順列^[9]は、集合をk個の山に分割し、それらをインターリーブする元である。 $(k,n)$ $S_{kn}$

と表記される -完全シャッフルは、 -完全シャッフルと-サイクルの合成であるため、の符号は次のようになります。 $(2,n)$ $\rho_{n}$ $(2,n-1)$ $n$ $\rho_{n}$

{\mbox{sgn}}(\rho _{n})=(-1)^{n+1}{\mbox{sgn}}(\rho _{n-1}).

したがって、符号は4周期です。

{\mbox{sgn}}(\rho _{n})=(-1)^{\lfloor n/2\rfloor }={\begin{cases}+1&n\equiv 0,1{\pmod {4}}\\-1&n\equiv 2,3{\pmod {4}}\end{cases}}

最初のいくつかの完全なシャッフルは次のとおりです。およびは自明であり、は転置です。 $\rho _{0}$ $\rho _{1}$ $\rho _{2}$ $(23)\in S_{4}$

注記

^ ディアコニス、グラハム、カンター 1983, 188
^ モリス 1998, 13
^ モリス 1998, 111
^ マスケリン 1894, 204
^ モリス 1998, 8
^ モリス 1998, 11–12
^ ディアコニス、グラハム、カンター 1983, 193
^ リアル数学とレクリエーション数学、ピーター・キャメロン、2014年4月10日。
^ エリス、ファン、シャリット 2002

参考文献

Diaconis, ペルシ島;グラハム, ロータリー州;カンター、W.M. (1983)。「完璧なシャッフルの数学」(PDF)。応用数学の進歩。4 (2): 175–196。土井: 10.1016/0196-8858(83)90009-X。

Ellis, J.; Fan, H.; Shallit, J. (2002). 「Multiway Perfect Shuffle Permutation のサイクル」(PDF) . Discrete Mathematics & Theoretical Computer Science . 5 308: 169– 180. doi :10.46298/dmtcs.308 . 2013年12月26日閲覧.

マスケリン、ジョン(1894). 『シャープス・アンド・フラッツ：チャンスとスキルが絡むゲームにおけるイカサマの秘密の完全暴露』ロングマンズ・グリーン・アンド・カンパニー. 2013年12月26日閲覧.

モリス、S. ブレント (1998). 『マジックトリック、カードシャッフル、そしてダイナミックコンピュータメモリ』アメリカ数学会. ISBN 0-883-85527-5. 2013年12月26日閲覧。

コラタ, ジーナ (1982年4月). 「パーフェクトシャッフルと数学との関係」. Science . 216 (4545): 505–506 . Bibcode :1982Sci...216..505K. doi :10.1126/science.216.4545.505. PMID 17735734.

Jain, Peiyush (2008年5月). 「インシャッフルのためのシンプルなインプレースアルゴリズム」. arXiv : 0805.1598 [cs.DS].

[1] ディアコニス、グラハム、カンター 1983, 188

[2] モリス 1998, 13

[3] モリス 1998, 111

[4] マスケリン 1894, 204

[5] モリス 1998, 8

[6] モリス 1998, 11–12

[7] ディアコニス、グラハム、カンター 1983, 193

[8] リアル数学とレクリエーション数学、ピーター・キャメロン、2014年4月10日。

[9] エリス、ファン、シャリット 2002