影響力のある観察
Observation that would cause a large change if deleted
アンスコムのカルテットでは、下段の2つのデータセットはどちらも影響力のある点を含んでいます。4つのデータセットは、単純な要約統計量で見ると全て同じように見えますが、グラフ化すると大きく異なります。1つの点を削除すると、線は大きく異なるものになります。

統計学において、影響力のある観測値とは、統計計算のための観測値であり、データセットからその観測値を削除すると計算結果が著しく変化するものである。 [1]特に、回帰分析において、影響力のある観測値とは、その削除がパラメータ推定値に大きな影響を与えるものである。[2]

評価

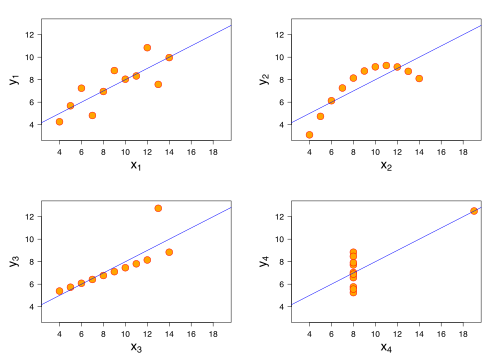
影響力を測定するための様々な方法が提案されている。[3] [4]推定回帰を仮定する。ここで、は応答変数のn ×1 列ベクトル、は説明変数（定数を含む）のn × k計画行列、はn ×1 残差ベクトル、は何らかの母数 の推定値のk ×1 ベクトルである。また、の射影行列を定義する。すると、以下の影響力の尺度が得られる。 y = X b + e {\displaystyle \mathbf {y} =\mathbf {X} \mathbf {b} +\mathbf {e} } y {\displaystyle \mathbf {y} } X {\displaystyle \mathbf {X} } e {\displaystyle \mathbf {e} } b {\displaystyle \mathbf {b} } β ∈ R k {\displaystyle \mathbf {\beta } \in \mathbb {R} ^{k}} H ≡ X ( X T X ) − 1 X T {\displaystyle \mathbf {H} \equiv \mathbf {X} \left(\mathbf {X} ^{\mathsf {T}}\mathbf {X} \right)^{-1}\mathbf {X} ^{\mathsf {T}}} X {\displaystyle \mathbf {X} }

  1. DFBETA i ≡ b − b ( − i ) = ( X T X ) − 1 x i T e i 1 − h i i {\displaystyle {\text{DFBETA}}_{i}\equiv \mathbf {b} -\mathbf {b} _{(-i)}={\frac {\left(\mathbf {X} ^{\mathsf {T}}\mathbf {X} \right)^{-1}\mathbf {x} _{i}^{\mathsf {T}}e_{i}}{1-h_{ii}}}} ここで、 はi番目の行を削除して推定された係数を表し、は行列の主対角線のi番目の値を表します。したがって、DFBETA は、影響点の有無による各パラメータ推定値の差を測定します。各変数と各観測値に対して DFBETA が存在します（N 個の観測値とk個の変数がある場合、N·k 個の DFBETA が存在します）。[5]表は、アンスコムのカルテットから 3 番目のデータセットの DFBETA を示しています（図の左下のグラフ）。 b ( − i ) {\displaystyle \mathbf {b} _{(-i)}} x i {\displaystyle \mathbf {x} _{i}} X {\displaystyle \mathbf {X} } h i i = x i ( X T X ) − 1 x i T {\displaystyle h_{ii}=\mathbf {x} _{i}\left(\mathbf {X} ^{\mathsf {T}}\mathbf {X} \right)^{-1}\mathbf {x} _{i}^{\mathsf {T}}} H {\displaystyle \mathbf {H} }
× y 傍受 スロープ
10.0 7.46 -0.005 -0.044
8.0 6.77 -0.037 0.019
13.0 12.74 -357.910 525.268
9.0 7.11 -0.033 0
11.0 7.81 0.049 -0.117
14.0 8.84 0.490 -0.667
6.0 6.08 0.027 -0.021
4.0 5.39 0.241 -0.209
12.0 8.15 0.137 -0.231
7.0 6.42 -0.020 0.013
5.0 5.73 0.105 -0.087
  1. DFFITS - 適合度の差
  2. クックのDは、データポイントを削除した場合の影響をすべてのパラメータの合計で測定します。[2]

アウトライアー、レバレッジ、影響力

外れ値は、他の観測値と著しく異なるデータポイントとして定義できます。 [6] [7] ハイレバレッジポイントは、独立変数の極端な値で行われた観測です。[8] どちらのタイプの非典型的な観測でも、回帰線はそのポイントに近くなります。[2] アンスコムのカルテットでは、右下の画像にはハイレバレッジのポイントがあり、左下の画像には外れ値のポイントがあります。

参照

参考文献

  1. ^ バート、ジェームズ・E.、バーバー、ジェラルド・M.、リグビー、デイビッド・L.（2009年）、地理学者のための初等統計学、ギルフォード・プレス、p.513、ISBN 9781572304840。
  2. ^ abc エヴェリット、ブライアン (1998). 『ケンブリッジ統計辞典』ケンブリッジ、イギリス、ニューヨーク:ケンブリッジ大学出版局. ISBN 0-521-59346-8。
  3. ^ Winner, Larry (2002年3月25日). 「影響統計、外れ値、共線性診断」
  4. ^ ベルズリー、デイビッド・A.、クー、エドウィン、ウェルシュ、ロイ・E. (1980). 回帰診断：影響力のあるデータと共線性の原因の特定. ワイリー確率・数理統計シリーズ. ニューヨーク：ジョン・ワイリー・アンド・サンズ. pp.  11– 16. ISBN 0-471-05856-4。
  5. ^ 「Outliers and DFBETA」（PDF） 。 2013年5月11日時点のオリジナルよりアーカイブ（PDF） 。
  6. ^ Grubbs, FE (1969年2月). 「サンプルにおける外れ値の検出手順」. Technometrics . 11 (1): 1– 21. doi :10.1080/00401706.1969.10490657.外れ値、または「外れ値」とは、それが存在するサンプル内の他のメンバーから著しく逸脱しているように見える値のことである。
  7. ^ Maddala, GS (1992). 「外れ値」. 計量経済学入門（第2版）. ニューヨーク: マクミラン. pp. 89. ISBN 978-0-02-374545-4外れ値とは、残りの観測値から大きく離れた観測値のことです。
  8. ^ Everitt, BS (2002). Cambridge Dictionary of Statistics . Cambridge University Press. ISBN 0-521-81099-X。

さらに読む

  • デホン、キャサリン；ガスナー、マージョリー；ヴェラルディ、ヴィンチェンツォ (2009). 「『良い』外れ値と過度に楽観的な結論に注意」オックスフォード経済統計速報71 (3): 437– 452. doi :10.1111/j.1468-0084.2009.00543.x. S2CID  154376487.
  • ケネディ、ピーター(2003). 「ロバスト推定」.計量経済学入門（第5版）. ケンブリッジ: MIT出版. pp.  372– 388. ISBN 0-262-61183-X。
Retrieved from "https://en.wikipedia.org/w/index.php?title=Influential_observation&oldid=1226593486"